九年级数学下2.5.1直线与圆的位置关系课件
文档属性
| 名称 | 九年级数学下2.5.1直线与圆的位置关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 13:54:14 | ||
图片预览




文档简介
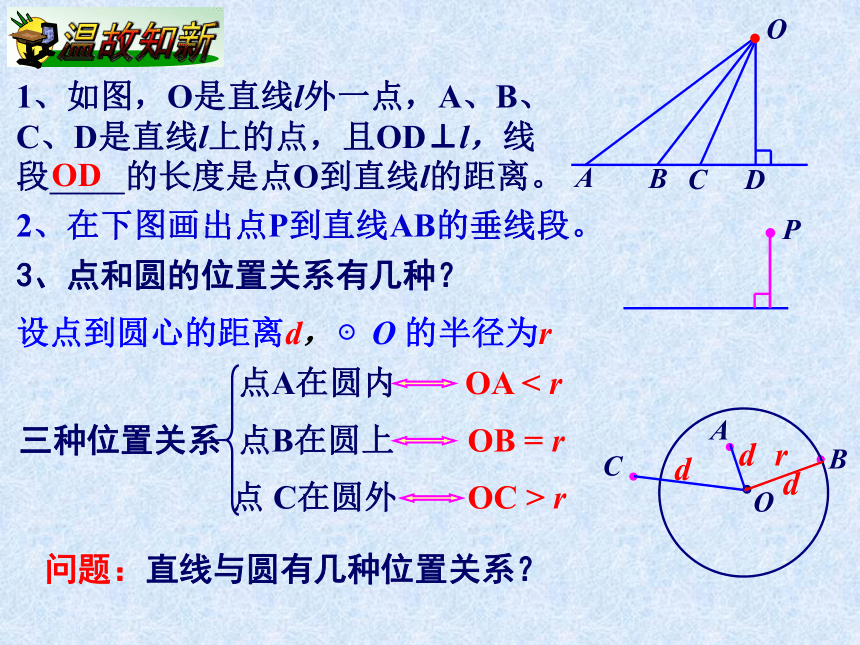
课件14张PPT。湘教版SHUXUE九年级下直线和圆的位置关系3、点和圆的位置关系有几种?设点到圆心的距离d,⊙O 的半径为r点A在圆内 点B在圆上点 C在圆外 OA < rOB = rOC > r1、如图,O是直线l外一点,A、B、C、D是直线l上的点,且OD⊥l,线段 的长度是点O到直线l的距离。OD2、在下图画出点P到直线AB的垂线段。问题:直线与圆有几种位置关系?地平线如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?你发现这个自然现象反映出直线和圆的公共点的个数
有 种情况。海上日出三种从海上日出抽象出哪些基本的几何图形?直线与圆的位置关系
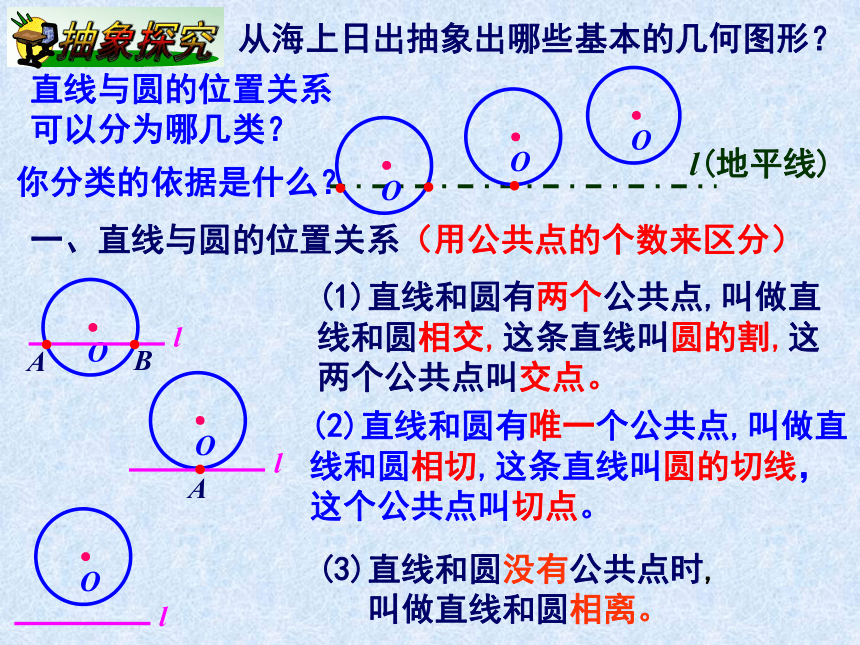
可以分为哪几类?l(地平线)一、直线与圆的位置关系(用公共点的个数来区分)(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割,这两个公共点叫交点。(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,
这个公共点叫切点。你分类的依据是什么?(3)直线和圆没有公共点时,
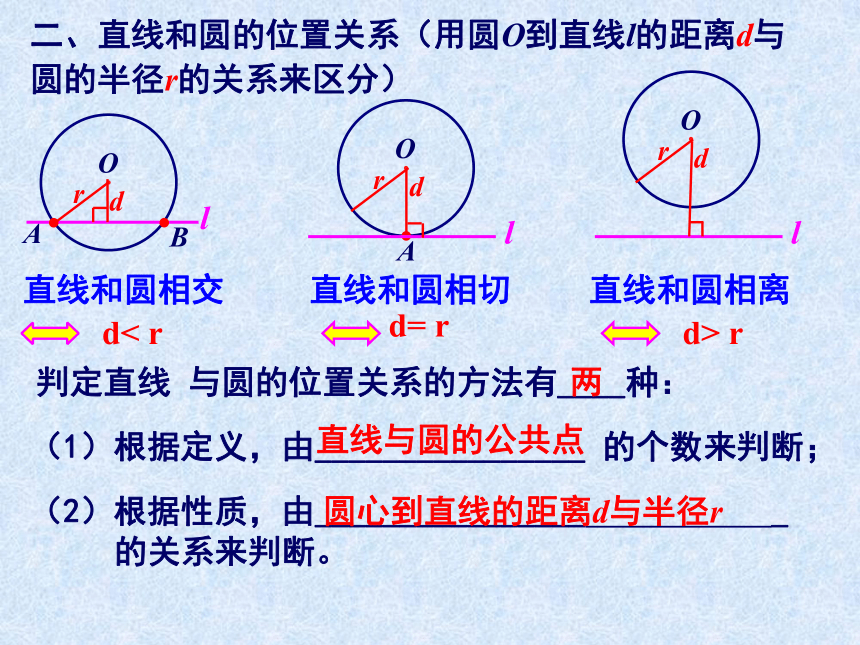
叫做直线和圆相离。二、直线和圆的位置关系(用圆O到直线l的距离d与圆的半径r的关系来区分)直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________ 的个数来判断;直线与圆的公共点 (2)根据性质,由________________ _ 的关系来判断。圆心到直线的距离d与半径r两2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交,则 。 相交相切相离d > 5cmd = 5cm0cm≤d<5cm2103、直线l和⊙O有公共点,则直线l与⊙O( )
A、相离;B、相切;C、相交;D、相切或相交。D4、如图,在Rt△ABC中,∠C=90°,
AB=5cm,AC=3cm,以C为圆心的圆与AB相切,则这个圆的半径是 cm。例1:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm; (2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d。CD=2.4cm当r=2cm时,⊙C与AB相离当r=2.4cm时,⊙C与AB相切当r=3cm时,⊙C与AB相交例2:设⊙O的圆心O到直线的距离为d,半径为r,d、r是方程(m+9)x2-(m+6)x+1=0的两根,且直线与⊙O相切时,求m的值?分析:直线与⊙O相切d=rb2-4ac=0解:由题意可得b2-4ac= [-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为:x2+ 2x+1=0x1=x2= -1(不符合题意舍去)当m=0时原方程 为:9x2-6x+1=0∴ m=0 例3、已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。43相离相切思考:若⊙A要与x轴相切,则⊙A该向上移动多少个单位?向上平移1个单位。若⊙A要与x轴相交呢?向上平移的距离: 1A相离 B相切 C相交 D都有可能4B3.已知圆O的直径为18cm,圆心O到直线l的距离为9cm,直线l与圆O的位置关系是 .相切4、已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .5、直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .d>5r>86、如图,已知∠BAC=30°,M为AC上一点,且AM=5cm,以M为圆心、r为半径的圆与直线AB有怎样的位置关系?(1) r=2cm(2) r=4cm(3) r=2.5cm2.5cm相交相切相离7、已知⊙O的半径r=7cm,直线l1 // l2,且l1与⊙O相切,圆心O到l2的距离为9cm.求l1与l2的距离.讨论题:在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,以C为圆心,r为半径作圆。①当r满足 时,直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
④当r满足 时, 线段AB与
⊙C只有一个公共点。13或5r2、判定直线与圆的位置关系的方法有____种:两(1)根据定义,由__________________的个数来判断;直线与圆的公共点(2)根据性质,由_____________________ 的关系来判断。圆心到直线的距离d与半径r
有 种情况。海上日出三种从海上日出抽象出哪些基本的几何图形?直线与圆的位置关系
可以分为哪几类?l(地平线)一、直线与圆的位置关系(用公共点的个数来区分)(1)直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割,这两个公共点叫交点。(2)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线,
这个公共点叫切点。你分类的依据是什么?(3)直线和圆没有公共点时,
叫做直线和圆相离。二、直线和圆的位置关系(用圆O到直线l的距离d与圆的半径r的关系来区分)直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________ 的个数来判断;直线与圆的公共点 (2)根据性质,由________________ _ 的关系来判断。圆心到直线的距离d与半径r两2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交,则 。 相交相切相离d > 5cmd = 5cm0cm≤d<5cm2103、直线l和⊙O有公共点,则直线l与⊙O( )
A、相离;B、相切;C、相交;D、相切或相交。D4、如图,在Rt△ABC中,∠C=90°,
AB=5cm,AC=3cm,以C为圆心的圆与AB相切,则这个圆的半径是 cm。例1:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB
有怎样的位置关系?为什么?
(1)r=2cm; (2)r=2.4cm (3)r=3cm.分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出C到AB的距离d。CD=2.4cm当r=2cm时,⊙C与AB相离当r=2.4cm时,⊙C与AB相切当r=3cm时,⊙C与AB相交例2:设⊙O的圆心O到直线的距离为d,半径为r,d、r是方程(m+9)x2-(m+6)x+1=0的两根,且直线与⊙O相切时,求m的值?分析:直线与⊙O相切d=rb2-4ac=0解:由题意可得b2-4ac= [-(m+6)]2-4(m+9)=0解得 m1= -8 m2= 0当m=-8时原方程 为:x2+ 2x+1=0x1=x2= -1(不符合题意舍去)当m=0时原方程 为:9x2-6x+1=0∴ m=0 例3、已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是_____。43相离相切思考:若⊙A要与x轴相切,则⊙A该向上移动多少个单位?向上平移1个单位。若⊙A要与x轴相交呢?向上平移的距离: 1
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
④当r满足 时, 线段AB与
⊙C只有一个公共点。13或5
