九年级数学下2.5.2圆的切线课件
图片预览



文档简介
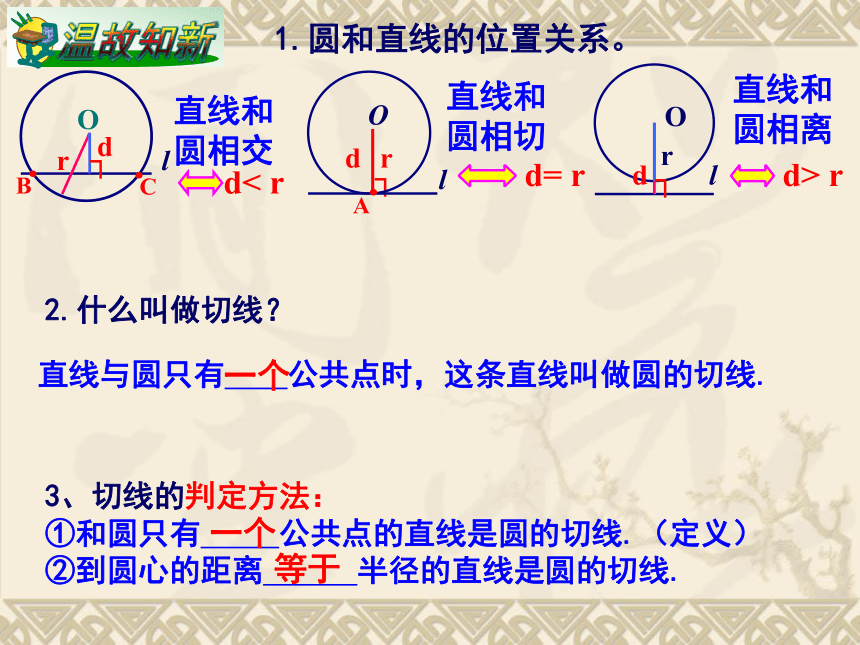
课件13张PPT。圆的切线1.圆和直线的位置关系。直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r2.什么叫做切线?直线与圆只有 公共点时,这条直线叫做圆的切线.一个3、切线的判定方法:
①和圆只有 公共点的直线是圆的切线.(定义)
②到圆心的距离 半径的直线是圆的切线.一个等于观察生活1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
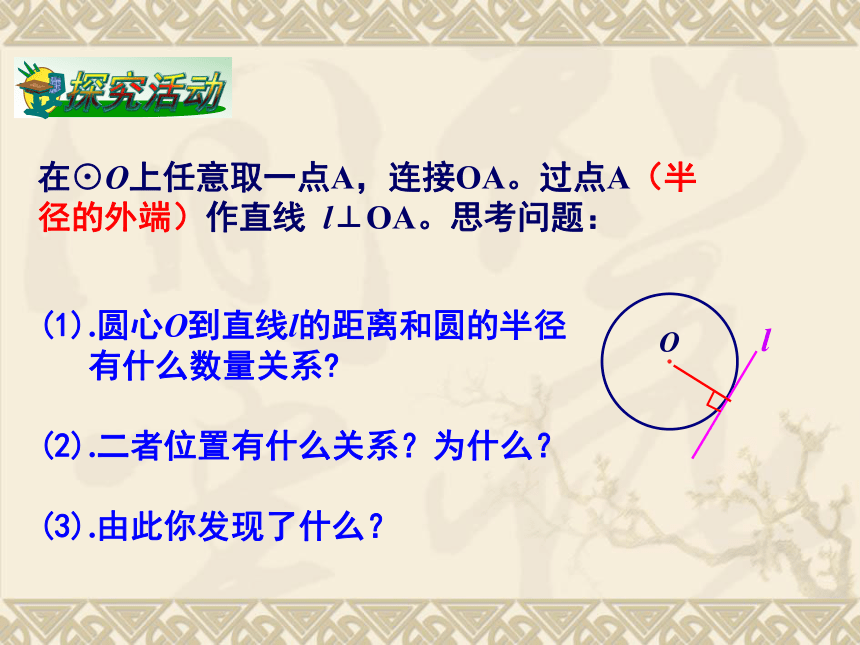
2.砂轮打磨工件飞出火星的方向是什么方向?在⊙O上任意取一点A,连接OA。过点A(半径的外端)作直线 l⊥OA。思考问题:(1).圆心O到直线l的距离和圆的半径
有什么数量关系?
(2).二者位置有什么关系?为什么?
(3).由此你发现了什么?切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。 切线需满足两条:
①经过半径外端;②垂直于这条半径.定理的几何语言:
∵ OA是半径, l ⊥ OA于点A ∴ l是⊙O的切线。判断右边图中直线l是⊙O切线吗?为什么?3、直线l与⊙O相切于点A,则过点A的
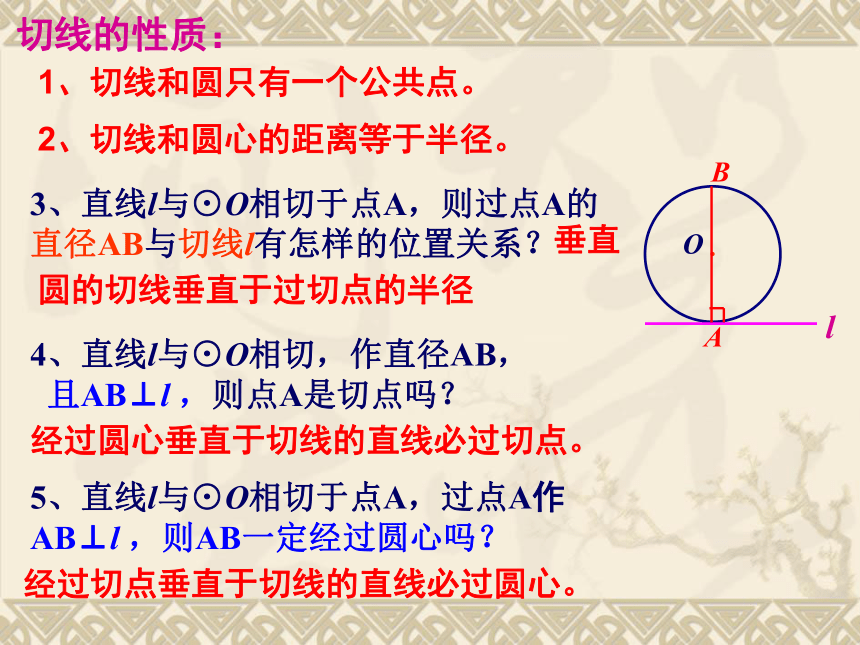
直径AB与切线l有怎样的位置关系?垂直切线的性质:圆的切线垂直于过切点的半径4、直线l与⊙O相切,作直径AB,
且AB⊥l ,则点A是切点吗?经过圆心垂直于切线的直线必过切点。5、直线l与⊙O相切于点A,过点A作AB⊥l ,则AB一定经过圆心吗?经过切点垂直于切线的直线必过圆心。1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。例1.已知:如图,直线AB经过圆O上的点C,并且OA=OB,AC=BC
求证:直线AB是圆O的切线.分析:已知AB经过圆上一点C,要证直线AB是圆O的切线.连结 ,证明 。OCOC⊥AB 证明:连接OC∵OA=OB∴ △OAB是等腰三角形又∵AC=BC∴OC⊥AB.(三线合一)∴AB是⊙O的切线.方法归纳:当直线与圆有公共点,常连结圆心和
公共点(半径),证明直线垂直于这条半径。连半径,证垂直例2、已知,如图,P是∠AOB的角平分线OC上的一点,
PE⊥OA于E,以P为圆心,PE长为半径作⊙P,
求证:OB是⊙P的切线。分析:OB与⊙P没有公共点,用判定定理。作 ,证明 。PD⊥OBPD的长等于半径证明:过P点,作PD⊥OB垂足为D,∵OC是∠AOB的角平分线,P在OC上。PE⊥OA∴PD=PE即:PD是⊙P的半径。∴OB是⊙P的切线.方法归纳:当直线与圆没有公共点,过圆心作直线
的垂线,证明圆心到直线的距离等于半径。作垂直,证半径1、已知:如图,AD是圆O的直径,直线BC经过点D,并且AB=AC, ∠BAD=∠CAD.
求证: 直线BC是圆O的切线.OD⊥BC.2、如图,AB是⊙O的直径,∠ABT=45°,AT=AB,求证:AT是⊙O的切线.∠BAT=90°3、求证:经过直径两端点的切线互相平行 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.求证: AC∥BDAB⊥ACAB⊥BD4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交⊙O于D,求证:BD是⊙O的切线。连OD,证OD⊥BD5、如图,已知AC是⊙O的直径且PA⊥AC,
BC是⊙O的一条弦,连结PB,PO
PO//BC,求证:PB是⊙O的切线。连结OB,
证明OB⊥PB6、如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,
DE是⊙O的切线,求证:DE⊥ACOD//AC,
DE⊥OD7、如图,已知AB是⊙O的直径,C是⊙O上一点,AD⊥CD,垂足为D,AC平分∠DAB,
(1).DC是⊙O的切线。
(2).若⊙O的半径是3,
AD=4,求AC的长。连OC,证∠OCD=90°连BC,
证?ADC∽?ACB1、判定直线与圆相切有哪些方法? ①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线2、切线性质:
(1)切线和圆只有一个公共点
(2)切线和圆心的距离等于半径。
(3)切线垂直于过切点的半径。
(4)经过圆心垂直于切线的直线必过切点。
(5)经过切点垂直于切线的直线必过圆心。3、方法归纳:
当直线与圆有公共点,常连结圆心和公共点(半径),证明直线垂直于这条半径。连半径,证垂直当直线与圆没有公共点,过圆心作直线的垂线,证明圆心到直线的距离等于半径。作垂直,证半径
①和圆只有 公共点的直线是圆的切线.(定义)
②到圆心的距离 半径的直线是圆的切线.一个等于观察生活1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨工件飞出火星的方向是什么方向?在⊙O上任意取一点A,连接OA。过点A(半径的外端)作直线 l⊥OA。思考问题:(1).圆心O到直线l的距离和圆的半径
有什么数量关系?
(2).二者位置有什么关系?为什么?
(3).由此你发现了什么?切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。 切线需满足两条:
①经过半径外端;②垂直于这条半径.定理的几何语言:
∵ OA是半径, l ⊥ OA于点A ∴ l是⊙O的切线。判断右边图中直线l是⊙O切线吗?为什么?3、直线l与⊙O相切于点A,则过点A的
直径AB与切线l有怎样的位置关系?垂直切线的性质:圆的切线垂直于过切点的半径4、直线l与⊙O相切,作直径AB,
且AB⊥l ,则点A是切点吗?经过圆心垂直于切线的直线必过切点。5、直线l与⊙O相切于点A,过点A作AB⊥l ,则AB一定经过圆心吗?经过切点垂直于切线的直线必过圆心。1、切线和圆只有一个公共点。2、切线和圆心的距离等于半径。例1.已知:如图,直线AB经过圆O上的点C,并且OA=OB,AC=BC
求证:直线AB是圆O的切线.分析:已知AB经过圆上一点C,要证直线AB是圆O的切线.连结 ,证明 。OCOC⊥AB 证明:连接OC∵OA=OB∴ △OAB是等腰三角形又∵AC=BC∴OC⊥AB.(三线合一)∴AB是⊙O的切线.方法归纳:当直线与圆有公共点,常连结圆心和
公共点(半径),证明直线垂直于这条半径。连半径,证垂直例2、已知,如图,P是∠AOB的角平分线OC上的一点,
PE⊥OA于E,以P为圆心,PE长为半径作⊙P,
求证:OB是⊙P的切线。分析:OB与⊙P没有公共点,用判定定理。作 ,证明 。PD⊥OBPD的长等于半径证明:过P点,作PD⊥OB垂足为D,∵OC是∠AOB的角平分线,P在OC上。PE⊥OA∴PD=PE即:PD是⊙P的半径。∴OB是⊙P的切线.方法归纳:当直线与圆没有公共点,过圆心作直线
的垂线,证明圆心到直线的距离等于半径。作垂直,证半径1、已知:如图,AD是圆O的直径,直线BC经过点D,并且AB=AC, ∠BAD=∠CAD.
求证: 直线BC是圆O的切线.OD⊥BC.2、如图,AB是⊙O的直径,∠ABT=45°,AT=AB,求证:AT是⊙O的切线.∠BAT=90°3、求证:经过直径两端点的切线互相平行 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.求证: AC∥BDAB⊥ACAB⊥BD4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交⊙O于D,求证:BD是⊙O的切线。连OD,证OD⊥BD5、如图,已知AC是⊙O的直径且PA⊥AC,
BC是⊙O的一条弦,连结PB,PO
PO//BC,求证:PB是⊙O的切线。连结OB,
证明OB⊥PB6、如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,
DE是⊙O的切线,求证:DE⊥ACOD//AC,
DE⊥OD7、如图,已知AB是⊙O的直径,C是⊙O上一点,AD⊥CD,垂足为D,AC平分∠DAB,
(1).DC是⊙O的切线。
(2).若⊙O的半径是3,
AD=4,求AC的长。连OC,证∠OCD=90°连BC,
证?ADC∽?ACB1、判定直线与圆相切有哪些方法? ①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线2、切线性质:
(1)切线和圆只有一个公共点
(2)切线和圆心的距离等于半径。
(3)切线垂直于过切点的半径。
(4)经过圆心垂直于切线的直线必过切点。
(5)经过切点垂直于切线的直线必过圆心。3、方法归纳:
当直线与圆有公共点,常连结圆心和公共点(半径),证明直线垂直于这条半径。连半径,证垂直当直线与圆没有公共点,过圆心作直线的垂线,证明圆心到直线的距离等于半径。作垂直,证半径
