九年级数学下2.5.4三角形的内切圆课件
文档属性
| 名称 | 九年级数学下2.5.4三角形的内切圆课件 |  | |
| 格式 | zip | ||
| 文件大小 | 432.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 14:08:36 | ||
图片预览





文档简介
课件12张PPT。三角形的内切圆湘教版SHUXUE九年级下1、确定圆的条件是什么?(1).圆心与半径(2).不在同一直线上的三点2、下图中△ABC与⊙O的关系?△ABC是⊙O的内接三角形;
⊙O是△ABC的外接圆
圆心O点叫△ABC的外心3、叙述角平分线的性质与判定性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上 如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?问题:怎样作圆,使它和三角形
三边都相切?讨论以下几个问题:(2)假设⊙I是所求作的圆,⊙I和三角形三边都相切,圆心I应满足什么条件?(3)这样的点I应在什么位置? (4)圆心I确定后半径如何找?(1)作圆的关键是什么?·MN如图,作⊙I,使它和三角形的各边都相切.口述作法定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。概念识记思考:一个三角形有几个内切圆?内心能否在三角形外部? 三角形三边中垂线的交点1.OA=OB=OC
2.外心不一定在三角形的内部三角形三条
角平分线的
交点1.到三边的距离相等2.OA、OB、OC分别平分三角。3.内心在三角形内部。外心:
三角形外接圆的圆心内心:
三角形内切圆的圆心比较:三角形外接圆和三角形内切圆三角形内心性质:内心三角形角平分线的交点。
内心到三角形三边的距离相等; 三角形外心的性质:外心到三角形各个顶点的距离相等;
外心在三角形三边的垂直平分线的交点;例1 如图,在△ABC中,点O是内心,
(1)若∠ABC=50°,∠ACB=70°,求∠BOC的度数解(1)∵点O是△ABC的内心,
∴ ∠OBC=∠OBA=25°
同理 ∠OCB=∠OCA=35°
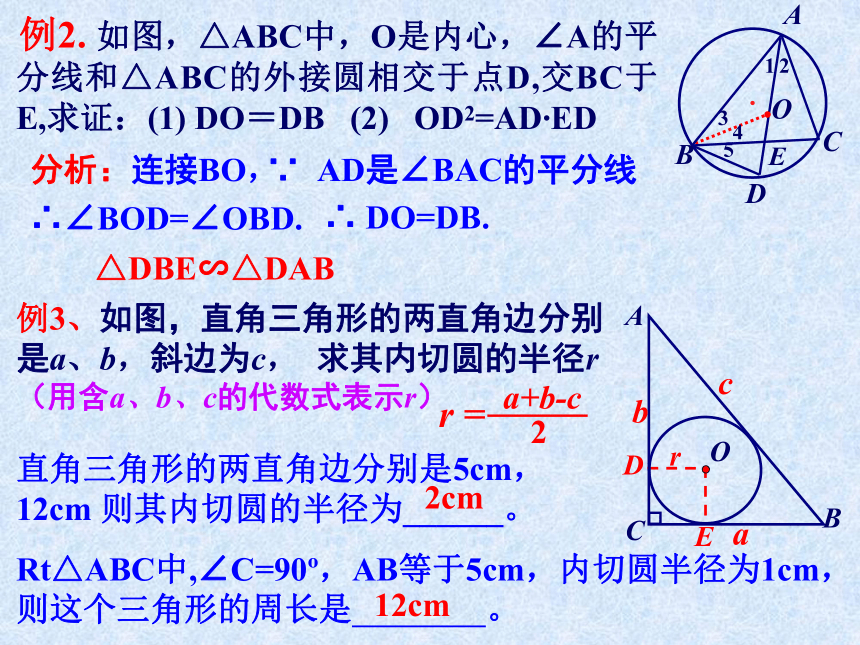
∴ ∠BOC=180°-(∠OBC+∠OCB)= 180°-60°=120° (2)若∠A=80°,则∠BOC= 。(3)若∠BOC=100°,则∠A= 。(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。130°20° 例2. 如图,△ABC中,O是内心,∠A的平分线和△ABC的外接圆相交于点D,交BC于E,求证:(1) DO=DB (2) OD2=AD?ED分析:连接BO,∵ AD是∠BAC的平分线∴∠BOD=∠OBD.∴ DO=DB.例3、如图,直角三角形的两直角边分别是a、b,斜边为c, 求其内切圆的半径r(用含a、b、c的代数式表示r)直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。2cmRt△ABC中,∠C=90o,AB等于5cm,内切圆半径为1cm,
则这个三角形的周长是 。12cm△DBE∽△DAB例4、已知,如图,△ABC的面积为S,三边长分别为a、b、c,求内切圆⊙O的半径 r.解:∵O是△ABC的内心。∴OD=OE=PF=rS=S△AOB+S△BOC+S△AOC6. 矩形一定有内切圆( )×判断题: 练 习1.三角形的内心到三角形各个顶点的距离相等( )2. 三角形的外心到三角形各边的距离相等 ( )3. 等边三角形的内心和外心重合; ( )4. 三角形的内心一定在三角形的内部( )5. 菱形一定有内切圆( )选择题:D××√√√提示:
等边三角形的内切圆与外接圆是两个同心圆。2、下列图形中,一定有内切圆的四边形是( ),
一定有外接圆的四边形是( )。
A. 梯形 B. 菱形 C. 矩形 D. 平行四边形BCD3.如图,PA、PB、DE分别切⊙O于
A、B、C,DE分别交PA,PB于D、
E,已知P到⊙O的切线长为8cm,
则Δ PDE的周长为( )
A 8cm B 12cm C 14cm D 16cm4.若直角三角形斜边长为10cm,其内切圆的半径为2cm,则它的周长为( )
A. 24cm B. 22cm C. 14cm D. 12cmA5、如图,四边形ABCD内切于⊙O,且AB=16,CD=10,则四边形的周长为( )
A. 50 B. 52 C. 54 D. 56B1.边长为3、4、5的三角形的内切圆的半径为 。2. 边长为5、5、6的三角形的内切圆的半径为 。3. 已知:△ABC的面积S=4cm2,周长等于10cm,则三角形内切圆的半径 。4.Rt△ABC中,∠C=90°,a=6,b=8,则内切圆的半径是_______.外接圆半径是 。25.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______.22cm填空题:511.50.8解答题:1.如图△ABC中,∠C=90?,AC=6,BC=8,三角形三边与⊙O均相切,切点分别是D、E、F,求⊙O的半径。 2.如图,△ABC中,∠C =90o ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F且BD=12,AD=8,求⊙O的半径r.3.△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.4.已知四边形ABCD的边AB、BC、CD、DA分别与⊙O相切于P、Q、M、N,求证:AB+CD=AD+BC。 5.三条公路AB、AC、BC两两相交与A、B、C三点(如图所示)。已知AC⊥BC,BC=3千米,AC=4千米。现想在△ABC内建一加油站M,使它到三条公路的距离相等,加油站M应建在离公路多远的地方?1、本节课从实际问题入手,探索得出三角形内切圆的作法 .
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,并介绍了多边形的内切圆、圆的外切多边形的概念。
3、学习 时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别,
4、利用三角形内心的性质解题时,要注意整体思想的运
用,在解决实际问题时,要注意把实际问题转化为数学问题。5、要记忆的知识点:直角三角形和任意三角形内切圆半径。三角形外接圆和内切圆的基本图形。
⊙O是△ABC的外接圆
圆心O点叫△ABC的外心3、叙述角平分线的性质与判定性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上 如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?问题:怎样作圆,使它和三角形
三边都相切?讨论以下几个问题:(2)假设⊙I是所求作的圆,⊙I和三角形三边都相切,圆心I应满足什么条件?(3)这样的点I应在什么位置? (4)圆心I确定后半径如何找?(1)作圆的关键是什么?·MN如图,作⊙I,使它和三角形的各边都相切.口述作法定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。概念识记思考:一个三角形有几个内切圆?内心能否在三角形外部? 三角形三边中垂线的交点1.OA=OB=OC
2.外心不一定在三角形的内部三角形三条
角平分线的
交点1.到三边的距离相等2.OA、OB、OC分别平分三角。3.内心在三角形内部。外心:
三角形外接圆的圆心内心:
三角形内切圆的圆心比较:三角形外接圆和三角形内切圆三角形内心性质:内心三角形角平分线的交点。
内心到三角形三边的距离相等; 三角形外心的性质:外心到三角形各个顶点的距离相等;
外心在三角形三边的垂直平分线的交点;例1 如图,在△ABC中,点O是内心,
(1)若∠ABC=50°,∠ACB=70°,求∠BOC的度数解(1)∵点O是△ABC的内心,
∴ ∠OBC=∠OBA=25°
同理 ∠OCB=∠OCA=35°
∴ ∠BOC=180°-(∠OBC+∠OCB)= 180°-60°=120° (2)若∠A=80°,则∠BOC= 。(3)若∠BOC=100°,则∠A= 。(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由。130°20° 例2. 如图,△ABC中,O是内心,∠A的平分线和△ABC的外接圆相交于点D,交BC于E,求证:(1) DO=DB (2) OD2=AD?ED分析:连接BO,∵ AD是∠BAC的平分线∴∠BOD=∠OBD.∴ DO=DB.例3、如图,直角三角形的两直角边分别是a、b,斜边为c, 求其内切圆的半径r(用含a、b、c的代数式表示r)直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。2cmRt△ABC中,∠C=90o,AB等于5cm,内切圆半径为1cm,
则这个三角形的周长是 。12cm△DBE∽△DAB例4、已知,如图,△ABC的面积为S,三边长分别为a、b、c,求内切圆⊙O的半径 r.解:∵O是△ABC的内心。∴OD=OE=PF=rS=S△AOB+S△BOC+S△AOC6. 矩形一定有内切圆( )×判断题: 练 习1.三角形的内心到三角形各个顶点的距离相等( )2. 三角形的外心到三角形各边的距离相等 ( )3. 等边三角形的内心和外心重合; ( )4. 三角形的内心一定在三角形的内部( )5. 菱形一定有内切圆( )选择题:D××√√√提示:
等边三角形的内切圆与外接圆是两个同心圆。2、下列图形中,一定有内切圆的四边形是( ),
一定有外接圆的四边形是( )。
A. 梯形 B. 菱形 C. 矩形 D. 平行四边形BCD3.如图,PA、PB、DE分别切⊙O于
A、B、C,DE分别交PA,PB于D、
E,已知P到⊙O的切线长为8cm,
则Δ PDE的周长为( )
A 8cm B 12cm C 14cm D 16cm4.若直角三角形斜边长为10cm,其内切圆的半径为2cm,则它的周长为( )
A. 24cm B. 22cm C. 14cm D. 12cmA5、如图,四边形ABCD内切于⊙O,且AB=16,CD=10,则四边形的周长为( )
A. 50 B. 52 C. 54 D. 56B1.边长为3、4、5的三角形的内切圆的半径为 。2. 边长为5、5、6的三角形的内切圆的半径为 。3. 已知:△ABC的面积S=4cm2,周长等于10cm,则三角形内切圆的半径 。4.Rt△ABC中,∠C=90°,a=6,b=8,则内切圆的半径是_______.外接圆半径是 。25.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______.22cm填空题:511.50.8解答题:1.如图△ABC中,∠C=90?,AC=6,BC=8,三角形三边与⊙O均相切,切点分别是D、E、F,求⊙O的半径。 2.如图,△ABC中,∠C =90o ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F且BD=12,AD=8,求⊙O的半径r.3.△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.4.已知四边形ABCD的边AB、BC、CD、DA分别与⊙O相切于P、Q、M、N,求证:AB+CD=AD+BC。 5.三条公路AB、AC、BC两两相交与A、B、C三点(如图所示)。已知AC⊥BC,BC=3千米,AC=4千米。现想在△ABC内建一加油站M,使它到三条公路的距离相等,加油站M应建在离公路多远的地方?1、本节课从实际问题入手,探索得出三角形内切圆的作法 .
2、通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,并介绍了多边形的内切圆、圆的外切多边形的概念。
3、学习 时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别,
4、利用三角形内心的性质解题时,要注意整体思想的运
用,在解决实际问题时,要注意把实际问题转化为数学问题。5、要记忆的知识点:直角三角形和任意三角形内切圆半径。三角形外接圆和内切圆的基本图形。
