九年级数学下2.6《弧长和扇形的面积》拓展课件
文档属性
| 名称 | 九年级数学下2.6《弧长和扇形的面积》拓展课件 |  | |
| 格式 | zip | ||
| 文件大小 | 223.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 14:11:41 | ||
图片预览



文档简介
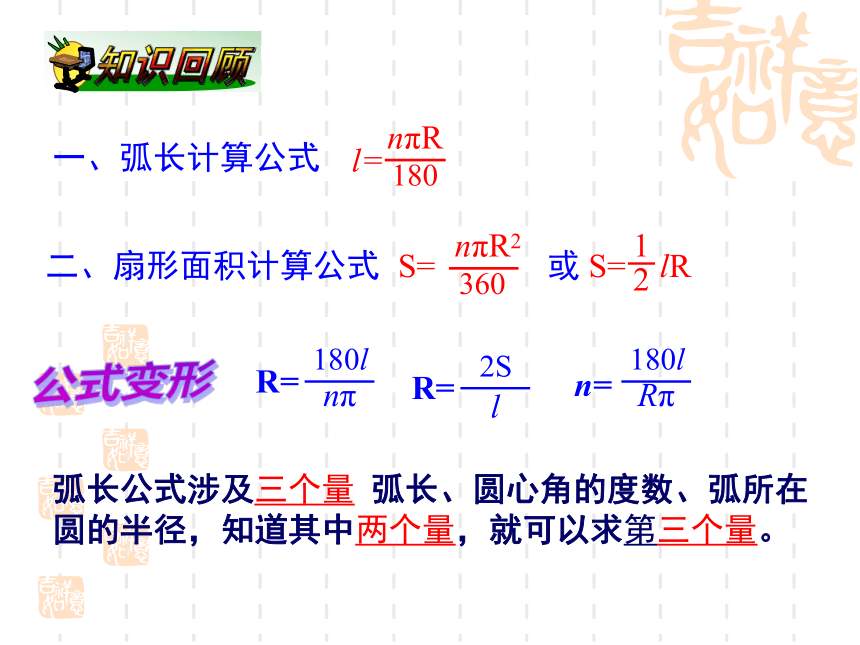
课件13张PPT。弧长和扇形面积----拓展训练二、扇形面积计算公式公式变形弧长公式涉及三个量 弧长、圆心角的度数、弧所在
圆的半径,知道其中两个量,就可以求第三个量。2、已知扇形的半径为6cm,扇形的弧长为πcm,
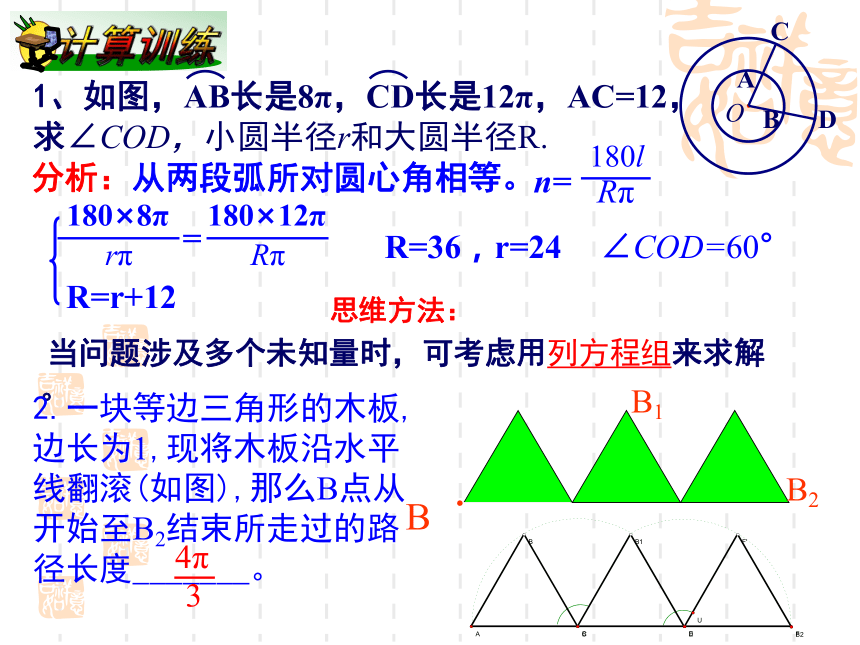
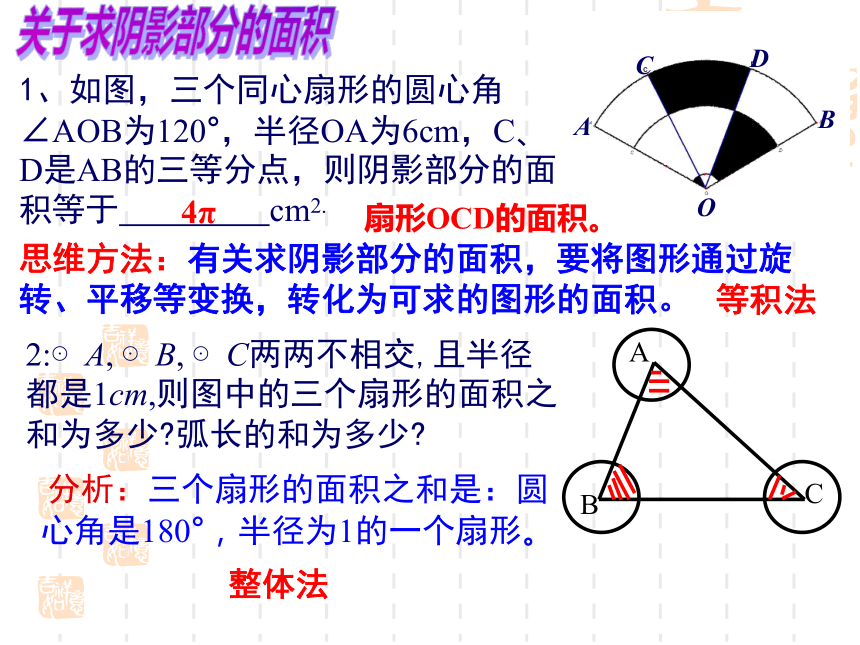
则该扇形的面积是______cm2,扇形的圆心角为______.3π30°45°2同 步 练 习:R=36,r=24∠COD=60°2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度_______。BB1B2解:连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴OECD为矩形,∠EOD=90°,OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△BDO.∴r =12,关于求阴影部分的面积1、如图,三个同心扇形的圆心角∠AOB为120°,半径OA为6cm,C、D是AB的三等分点,则阴影部分的面积等于 cm2.思维方法:有关求阴影部分的面积,要将图形通过旋转、平移等变换,转化为可求的图形的面积。扇形OCD的面积。4π2:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少? 整体法分析:三个扇形的面积之和是:圆心角是180°,半径为1的一个扇形。等积法分析:S阴影=S?ABC-3S扇形作差法4、如图,在Rt?ABC中,∠ABC=90°,AB=BC=2,以BC为直径的圆交AC于D,则图中阴影部分的面积是多少?分析:连结BD,阴影部分的面积
等于?ABD的面积。割补法1. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为____。160°3.如图:AB是半圆的直径,AB=2r, C、D是半圆的三等分点,阴影部分的面积等于 。 4、如图,两个同心圆中,大圆的半径OA=4cm,∠AOB=∠BOC=60°,
则图中阴影部分的面积是______cm2。2、如图,已知扇形的圆心角为150°,弧长为20πcm,
则扇形的半径是 .24cm5.有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81°,求这段圆弧的半径R(精确到0.1m).6、一段圆弧形的公路弯道,圆弧的半径是2千米.一辆汽车以每小时60公里的速度通过弯道,需时间20秒, 试求弯道(弧AB)所对圆心角的度数(结果精确到0.1度).2千米?9.5°7、如图,⊙A、 ⊙B、 ⊙C、 ⊙D、⊙E两两不相交,且半径都是2cm,求五个扇形的面积之和及弧长之和。 8、如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.9、如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,
∠P=60°,求图中阴影部分的面积。10、A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,求阴影部分面积。11、如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。弓形的面积=S扇+S△弓形的面积=S扇-S△2.扇形面积公式与弧长公式的区别:1. 弧长、扇形的面积与哪些因素有关?(1)与圆心角的大小有关(2)与半径的长短有关3.扇形面积公式、弧长公式与圆心角、半径的互化:4、求弧长、阴影部分面积的思维方法。(2)有关求阴影部分的面积,要将图形通过旋转、平移等变换,转化为可求的图形的面积。等积法整体法作差法割补法 (1)当问题涉及多个未知量时,可考虑用列方程组来求解布置作业:课堂作业:第82页5、6、7题
课外作业:《学法大视野》
圆的半径,知道其中两个量,就可以求第三个量。2、已知扇形的半径为6cm,扇形的弧长为πcm,
则该扇形的面积是______cm2,扇形的圆心角为______.3π30°45°2同 步 练 习:R=36,r=24∠COD=60°2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度_______。BB1B2解:连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴OECD为矩形,∠EOD=90°,OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△BDO.∴r =12,关于求阴影部分的面积1、如图,三个同心扇形的圆心角∠AOB为120°,半径OA为6cm,C、D是AB的三等分点,则阴影部分的面积等于 cm2.思维方法:有关求阴影部分的面积,要将图形通过旋转、平移等变换,转化为可求的图形的面积。扇形OCD的面积。4π2:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少? 整体法分析:三个扇形的面积之和是:圆心角是180°,半径为1的一个扇形。等积法分析:S阴影=S?ABC-3S扇形作差法4、如图,在Rt?ABC中,∠ABC=90°,AB=BC=2,以BC为直径的圆交AC于D,则图中阴影部分的面积是多少?分析:连结BD,阴影部分的面积
等于?ABD的面积。割补法1. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的圆心角为____。160°3.如图:AB是半圆的直径,AB=2r, C、D是半圆的三等分点,阴影部分的面积等于 。 4、如图,两个同心圆中,大圆的半径OA=4cm,∠AOB=∠BOC=60°,
则图中阴影部分的面积是______cm2。2、如图,已知扇形的圆心角为150°,弧长为20πcm,
则扇形的半径是 .24cm5.有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81°,求这段圆弧的半径R(精确到0.1m).6、一段圆弧形的公路弯道,圆弧的半径是2千米.一辆汽车以每小时60公里的速度通过弯道,需时间20秒, 试求弯道(弧AB)所对圆心角的度数(结果精确到0.1度).2千米?9.5°7、如图,⊙A、 ⊙B、 ⊙C、 ⊙D、⊙E两两不相交,且半径都是2cm,求五个扇形的面积之和及弧长之和。 8、如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.9、如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,
∠P=60°,求图中阴影部分的面积。10、A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,求阴影部分面积。11、如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。弓形的面积=S扇+S△弓形的面积=S扇-S△2.扇形面积公式与弧长公式的区别:1. 弧长、扇形的面积与哪些因素有关?(1)与圆心角的大小有关(2)与半径的长短有关3.扇形面积公式、弧长公式与圆心角、半径的互化:4、求弧长、阴影部分面积的思维方法。(2)有关求阴影部分的面积,要将图形通过旋转、平移等变换,转化为可求的图形的面积。等积法整体法作差法割补法 (1)当问题涉及多个未知量时,可考虑用列方程组来求解布置作业:课堂作业:第82页5、6、7题
课外作业:《学法大视野》
