人教版物理必修1同步教学课件:第3章 4力的合成29张PPT
文档属性
| 名称 | 人教版物理必修1同步教学课件:第3章 4力的合成29张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 891.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-12-26 16:54:55 | ||
图片预览








文档简介
(共29张PPT)
5 力的合成
第三章 相互作用
学习目标
1.知道合力与分力的概念及力的合成的概念.
2.理解平行四边形定则是一切矢量合成的普遍法则,会用平行四边形定则求合力,知道分力与合力间的大小关系.
3.知道共点力的概念,会用作图法、计算法求合力.
一、力的合成
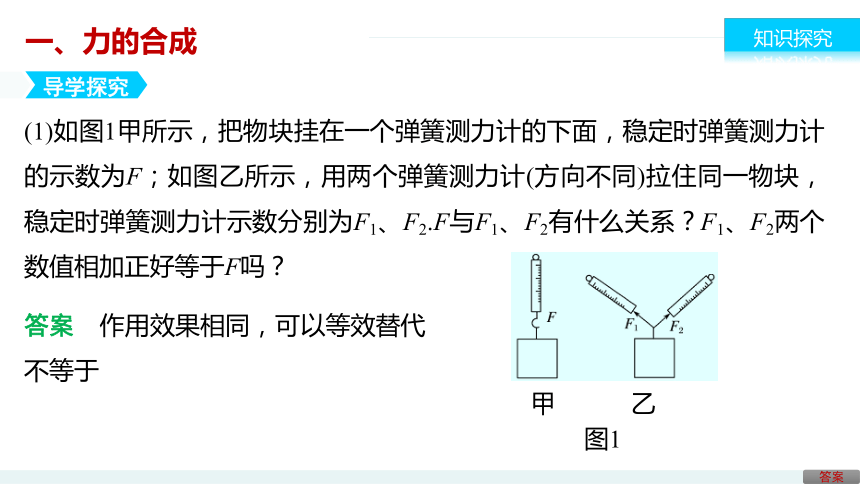
(1)如图1甲所示,把物块挂在一个弹簧测力计的下面,稳定时弹簧测力计的示数为F;如图乙所示,用两个弹簧测力计(方向不同)拉住同一物块,稳定时弹簧测力计示数分别为F1、F2.F与F1、F2有什么关系?F1、F2两个数值相加正好等于F吗?
导学探究
图1
甲 乙
答案 作用效果相同,可以等效替代 不等于
答案
(2)做一做:按课本“实验”提供的“探究求合力的方法”,回答下列问题:
①两次实验要把小圆环拉到同一位置,这体现了什么物理思想?
②严格按照力的图示法作出两分力F1、F2及它们的合力F.用虚线把合力F的箭头端分别与两个分力的箭头端连接,所成的图形是什么?
答案 ①等效替代 ②平行四边形
答案
对力的合成的理解
(1)合力与分力
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的 跟原来几个力的共同效果 ,这个力就叫做那几个力的 ,原来的几个力叫做 .
(2)力的合成的方法——平行四边形定则:
求两个互成角度的共点力F1、F2的合力,可以把F1、F2的线段作为邻边作平行四边形,这两个邻边之间的对角线即表示合力的大小和方向.
知识梳理
效果
相同
合力
分力
答案
关于合力的下述说法中正确的是( )
A.合力的性质与原来分力性质相同
B.合力与原来的分力间的关系是等效替代关系
C.合力总比分力大
D.合力总比一个分力大,比另一个分力小
即学即用
解析 在力的合成中,合力并不是一个真实存在的力,找不到合力的施力者,合力与分力的概念是建立在效果相同即所谓的等效的基础上的,因此,合力也就没有性质的问题.合力这个“合”字的意义不是代数中的“和”,合力F既可以大于、也可以等于或小于原来的任意一个分力,一般地,|F1-F2|≤F≤F1+F2.故正确选项为B.
B
解析答案
二、共点力及其平衡
(1)共点力一定作用在同一点吗?
导学探究
答案 不一定,有可能是延长线(或反向延长线)交于一点.
(2)物体在两个力作用下处于平衡状态,这两个力有什么关系?物体在三个共点力作用下处于平衡状态,这三个力有什么关系?
答案 两个力等大反向,合力为零;三个力作用下处于平衡状态,其中两个力的合力与第三个力等大反向.
答案
共点力及其平衡
(1)共点力:如果几个力共同作用在 上,或者虽不作用在同一点上,但它们的 ,这样的一组力叫做共点力.力的合成的平行四边形定则,只适用于共点力.
(2)平衡状态:物体处于 或 的状态.物体处于平衡状态时F合= .
知识梳理
同一点
延长线交于一点
静止
匀速直线运动
0
答案
关于共点力,下列说法中错误的是( )
A.作用在一个物体上的两个力,如果大小相等,方向相反,则这两个力一
定是共点力
B.作用在一个物体上的两个力,如果是一对平衡力,则这两个力是共点力
C.作用在一个物体上的几个力,如果它们的作用点在同一点上,则这几个
力是共点力
D.作用在一个物体上的几个力,如果它们的作用线交于同一点,则这几个
力是共点力
即学即用
解析答案
返回
解析 共点力是指同时作用在物体上的同一点或作用线相交于同一点的几个力,故A错误,B、C、D正确.
答案 A
返回
例1 关于两个大小不变的共点力F1、F2与其合力F的关系,下列说法中正确的是( )
A.F大小随F1、F2间夹角的增大而增大
B.F大小随F1、F2间夹角的增大而减小
C.F大小一定小于F1、F2中最大者
D.F大小不能小于F1、F2中最小者
一、合力与分力的关系
总结提升
解析答案
解析 合力随两分力间夹角的增大而减小,合力大小的范围为|F1-F2|≤F≤F1+F2,例如,当F1=5 N、F2=6 N时,1 N≤F≤11 N,F可比F1、F2中的最小者小,也可以比F1、F2中的最大者大,故选项B正确.
B
总结提升
合力与分力的大小关系
合力F既可以大于、也可以等于或小于原来的任意一个分力.
两分力大小不变时,合力F随夹角α的增大而减小,随α的减小而增大.
(1)F的最大值:当α=0时,Fmax=F1+F2;
(2)F的最小值:当α=180°时,Fmin=|F1-F2|;
(3)合力大小的取值范围:|F1-F2|≤F≤F1+F2.
例2 在电线杆的两侧常用钢丝绳把它固定在地上,如图2所示.如果钢丝绳与地面的夹角∠A=∠B=60°,每条钢丝绳的拉力都是300 N,分别用作图法和计算法求两根钢丝绳作用在电线杆上的合力.(保留三位有效数字)
二、两力合成的基本方法
归纳总结
解析答案
图2
解析 解法一:作图法
如图甲所示,自O点引两条有向线段OC和OD,夹角为60°.设定每单位长度表示100 N,则OC和OD的长度都是3个单位长度,作出平行四边形OCED,其对角线OE就表示两个拉力F1、F2的合力F,量得OE长约为5.2个单位长度,所以合力F≈100×5.2 N=520 N.
用量角器量得∠COE=∠DOE=30°,所以合力方向竖直向下.
甲
归纳总结
解析答案
解法二:计算法
先画出力的平行四边形,如图乙所示,其对角线OE就表示两个拉力F1、F2的合力F,由于OC=OD,因此得到的是菱形,再连接CD,两对角线垂直且平分,∠COO′=30°.在三角形OCO′中OO′=OCcos 30°.
乙
归纳总结
归纳总结
1.作图法(如图3所示)
图3
归纳总结
2.计算法
(1)两分力共线时:
①若F1、F2两力同向,则合力F=F1+F2,方向与两力同向.
②若F1、F2两力反向,则合力F=|F1-F2|,方向与两力中较大的同向.
(2)两分力不共线时:
可以根据平行四边形定则作出力的示意图,然后由几何关系求解对角线,其长度即为合力大小.以下为两种特殊情况.
归纳总结
归纳总结
图4
图5
若α=120°,则合力大小等于分力大小
(如图6所示).
图6
例3 小娟、小明两人共提一桶水匀速前行,如图7所示,已知两人手臂上的拉力大小相等且为F,两人手臂间的夹角为θ,水和水桶的总重力为G,则下列说法中正确的是( )
三、共点力及其平衡
总结提升
解析答案
图7
返回
总结提升
θ越大,在合力一定时,分力越大,故D错.
答案 C
总结提升
共点力平衡的几条重要推论:
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,这两个力必定大小相等、方向相反.
(2)三力平衡:①物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力等大反向.②三个力可以构成首尾相连的矢量三角形.
(3)多力平衡:物体受N个共点力作用下处于平衡状态时,其中任意一个力与剩余N-1个力的合力一定等大反向.
返回
1.两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能等于( )
A.9 N B.25 N C.8 N D.21 N
解析 F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此范围的是25 N,应选择B项.
B
解析答案
2.如图所示,三个大小相等的力F,作用于同一点O,则合力最小的是( )
C
答案
3.(多选)如图8所示,两根等长的轻绳将日光灯悬挂在天花板上,两绳与竖直方向的夹角都为45°,日光灯保持水平,所受重力为G.则( )
图8
A.两绳对日光灯拉力的合力大小为G
B.两绳的拉力和重力不是共点力
解析答案
解析 如图,两绳拉力的作用线与重力作用线的延长线交于一点,这三个力为共点力,B选项错误;
由于日光灯在两绳拉力和重力作用下处于平衡状态,所以两绳的拉力的合力与重力G等大反向,A选项正确;
答案 AC
4.物体只受两个力F1和F2的作用,F1=30 N,方向水平向左,F2=40 N,方向竖直向下,求这两个力的合力F.
解析答案
返回
解析 解法一 作图法
设定每单位长度表示10 N,则分别取3个单位长度、4个单位长度,自O点引两条有向线段OF1和OF2分别表示力F1、F2.以OF1和OF2为两个邻边作平行四边形如图所示,
则对角线OF就是所求的合力F.量出对角线的长度为5个单位长度,则合力的大小F=5×10 N=50 N.用量角器量出合力F与分力F1的夹角θ为53°,方向斜向左下.
解析答案
解法二 计算法
返回
答案 50 N,方向为与F1的夹角成53°角斜向左下方
5 力的合成
第三章 相互作用
学习目标
1.知道合力与分力的概念及力的合成的概念.
2.理解平行四边形定则是一切矢量合成的普遍法则,会用平行四边形定则求合力,知道分力与合力间的大小关系.
3.知道共点力的概念,会用作图法、计算法求合力.
一、力的合成
(1)如图1甲所示,把物块挂在一个弹簧测力计的下面,稳定时弹簧测力计的示数为F;如图乙所示,用两个弹簧测力计(方向不同)拉住同一物块,稳定时弹簧测力计示数分别为F1、F2.F与F1、F2有什么关系?F1、F2两个数值相加正好等于F吗?
导学探究
图1
甲 乙
答案 作用效果相同,可以等效替代 不等于
答案
(2)做一做:按课本“实验”提供的“探究求合力的方法”,回答下列问题:
①两次实验要把小圆环拉到同一位置,这体现了什么物理思想?
②严格按照力的图示法作出两分力F1、F2及它们的合力F.用虚线把合力F的箭头端分别与两个分力的箭头端连接,所成的图形是什么?
答案 ①等效替代 ②平行四边形
答案
对力的合成的理解
(1)合力与分力
当一个物体受到几个力的共同作用时,我们常常可以求出这样一个力,这个力产生的 跟原来几个力的共同效果 ,这个力就叫做那几个力的 ,原来的几个力叫做 .
(2)力的合成的方法——平行四边形定则:
求两个互成角度的共点力F1、F2的合力,可以把F1、F2的线段作为邻边作平行四边形,这两个邻边之间的对角线即表示合力的大小和方向.
知识梳理
效果
相同
合力
分力
答案
关于合力的下述说法中正确的是( )
A.合力的性质与原来分力性质相同
B.合力与原来的分力间的关系是等效替代关系
C.合力总比分力大
D.合力总比一个分力大,比另一个分力小
即学即用
解析 在力的合成中,合力并不是一个真实存在的力,找不到合力的施力者,合力与分力的概念是建立在效果相同即所谓的等效的基础上的,因此,合力也就没有性质的问题.合力这个“合”字的意义不是代数中的“和”,合力F既可以大于、也可以等于或小于原来的任意一个分力,一般地,|F1-F2|≤F≤F1+F2.故正确选项为B.
B
解析答案
二、共点力及其平衡
(1)共点力一定作用在同一点吗?
导学探究
答案 不一定,有可能是延长线(或反向延长线)交于一点.
(2)物体在两个力作用下处于平衡状态,这两个力有什么关系?物体在三个共点力作用下处于平衡状态,这三个力有什么关系?
答案 两个力等大反向,合力为零;三个力作用下处于平衡状态,其中两个力的合力与第三个力等大反向.
答案
共点力及其平衡
(1)共点力:如果几个力共同作用在 上,或者虽不作用在同一点上,但它们的 ,这样的一组力叫做共点力.力的合成的平行四边形定则,只适用于共点力.
(2)平衡状态:物体处于 或 的状态.物体处于平衡状态时F合= .
知识梳理
同一点
延长线交于一点
静止
匀速直线运动
0
答案
关于共点力,下列说法中错误的是( )
A.作用在一个物体上的两个力,如果大小相等,方向相反,则这两个力一
定是共点力
B.作用在一个物体上的两个力,如果是一对平衡力,则这两个力是共点力
C.作用在一个物体上的几个力,如果它们的作用点在同一点上,则这几个
力是共点力
D.作用在一个物体上的几个力,如果它们的作用线交于同一点,则这几个
力是共点力
即学即用
解析答案
返回
解析 共点力是指同时作用在物体上的同一点或作用线相交于同一点的几个力,故A错误,B、C、D正确.
答案 A
返回
例1 关于两个大小不变的共点力F1、F2与其合力F的关系,下列说法中正确的是( )
A.F大小随F1、F2间夹角的增大而增大
B.F大小随F1、F2间夹角的增大而减小
C.F大小一定小于F1、F2中最大者
D.F大小不能小于F1、F2中最小者
一、合力与分力的关系
总结提升
解析答案
解析 合力随两分力间夹角的增大而减小,合力大小的范围为|F1-F2|≤F≤F1+F2,例如,当F1=5 N、F2=6 N时,1 N≤F≤11 N,F可比F1、F2中的最小者小,也可以比F1、F2中的最大者大,故选项B正确.
B
总结提升
合力与分力的大小关系
合力F既可以大于、也可以等于或小于原来的任意一个分力.
两分力大小不变时,合力F随夹角α的增大而减小,随α的减小而增大.
(1)F的最大值:当α=0时,Fmax=F1+F2;
(2)F的最小值:当α=180°时,Fmin=|F1-F2|;
(3)合力大小的取值范围:|F1-F2|≤F≤F1+F2.
例2 在电线杆的两侧常用钢丝绳把它固定在地上,如图2所示.如果钢丝绳与地面的夹角∠A=∠B=60°,每条钢丝绳的拉力都是300 N,分别用作图法和计算法求两根钢丝绳作用在电线杆上的合力.(保留三位有效数字)
二、两力合成的基本方法
归纳总结
解析答案
图2
解析 解法一:作图法
如图甲所示,自O点引两条有向线段OC和OD,夹角为60°.设定每单位长度表示100 N,则OC和OD的长度都是3个单位长度,作出平行四边形OCED,其对角线OE就表示两个拉力F1、F2的合力F,量得OE长约为5.2个单位长度,所以合力F≈100×5.2 N=520 N.
用量角器量得∠COE=∠DOE=30°,所以合力方向竖直向下.
甲
归纳总结
解析答案
解法二:计算法
先画出力的平行四边形,如图乙所示,其对角线OE就表示两个拉力F1、F2的合力F,由于OC=OD,因此得到的是菱形,再连接CD,两对角线垂直且平分,∠COO′=30°.在三角形OCO′中OO′=OCcos 30°.
乙
归纳总结
归纳总结
1.作图法(如图3所示)
图3
归纳总结
2.计算法
(1)两分力共线时:
①若F1、F2两力同向,则合力F=F1+F2,方向与两力同向.
②若F1、F2两力反向,则合力F=|F1-F2|,方向与两力中较大的同向.
(2)两分力不共线时:
可以根据平行四边形定则作出力的示意图,然后由几何关系求解对角线,其长度即为合力大小.以下为两种特殊情况.
归纳总结
归纳总结
图4
图5
若α=120°,则合力大小等于分力大小
(如图6所示).
图6
例3 小娟、小明两人共提一桶水匀速前行,如图7所示,已知两人手臂上的拉力大小相等且为F,两人手臂间的夹角为θ,水和水桶的总重力为G,则下列说法中正确的是( )
三、共点力及其平衡
总结提升
解析答案
图7
返回
总结提升
θ越大,在合力一定时,分力越大,故D错.
答案 C
总结提升
共点力平衡的几条重要推论:
(1)二力平衡:如果物体在两个共点力的作用下处于平衡状态,这两个力必定大小相等、方向相反.
(2)三力平衡:①物体在三个共点力作用下处于平衡状态时,任意两个力的合力与第三个力等大反向.②三个力可以构成首尾相连的矢量三角形.
(3)多力平衡:物体受N个共点力作用下处于平衡状态时,其中任意一个力与剩余N-1个力的合力一定等大反向.
返回
1.两个共点力的大小分别为F1=15 N,F2=8 N,它们的合力大小不可能等于( )
A.9 N B.25 N C.8 N D.21 N
解析 F1、F2的合力范围是|F1-F2|≤F≤F1+F2,故7 N≤F≤23 N,不在此范围的是25 N,应选择B项.
B
解析答案
2.如图所示,三个大小相等的力F,作用于同一点O,则合力最小的是( )
C
答案
3.(多选)如图8所示,两根等长的轻绳将日光灯悬挂在天花板上,两绳与竖直方向的夹角都为45°,日光灯保持水平,所受重力为G.则( )
图8
A.两绳对日光灯拉力的合力大小为G
B.两绳的拉力和重力不是共点力
解析答案
解析 如图,两绳拉力的作用线与重力作用线的延长线交于一点,这三个力为共点力,B选项错误;
由于日光灯在两绳拉力和重力作用下处于平衡状态,所以两绳的拉力的合力与重力G等大反向,A选项正确;
答案 AC
4.物体只受两个力F1和F2的作用,F1=30 N,方向水平向左,F2=40 N,方向竖直向下,求这两个力的合力F.
解析答案
返回
解析 解法一 作图法
设定每单位长度表示10 N,则分别取3个单位长度、4个单位长度,自O点引两条有向线段OF1和OF2分别表示力F1、F2.以OF1和OF2为两个邻边作平行四边形如图所示,
则对角线OF就是所求的合力F.量出对角线的长度为5个单位长度,则合力的大小F=5×10 N=50 N.用量角器量出合力F与分力F1的夹角θ为53°,方向斜向左下.
解析答案
解法二 计算法
返回
答案 50 N,方向为与F1的夹角成53°角斜向左下方
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
