北师大版八年级数学上7.4平行线的性质课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上7.4平行线的性质课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 590.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 14:08:12 | ||
图片预览





文档简介
课件21张PPT。7.4 平行线的性质 会根据“两直线平行,同位角相等”证明“两直线平行,内错角相等”和“两直线平行,同旁内角互补”,并能简单地应用这些结论. 角之间的关系 两直线平行平行线的判定公理 同位角相等,两直线平行定理 同旁内角互补,两直线平行定理 内错角相等,两直线平行 根据“两条平行线被第三条直线所截,同位角相等”.你能作出相关的图形吗?你能说说证明的思路吗? 你能根据所作的图形写出已知、求证吗?平行线的性质两直线平行,同位角相等. 两条平行线被第三条直线所截,同位角相等。
↓
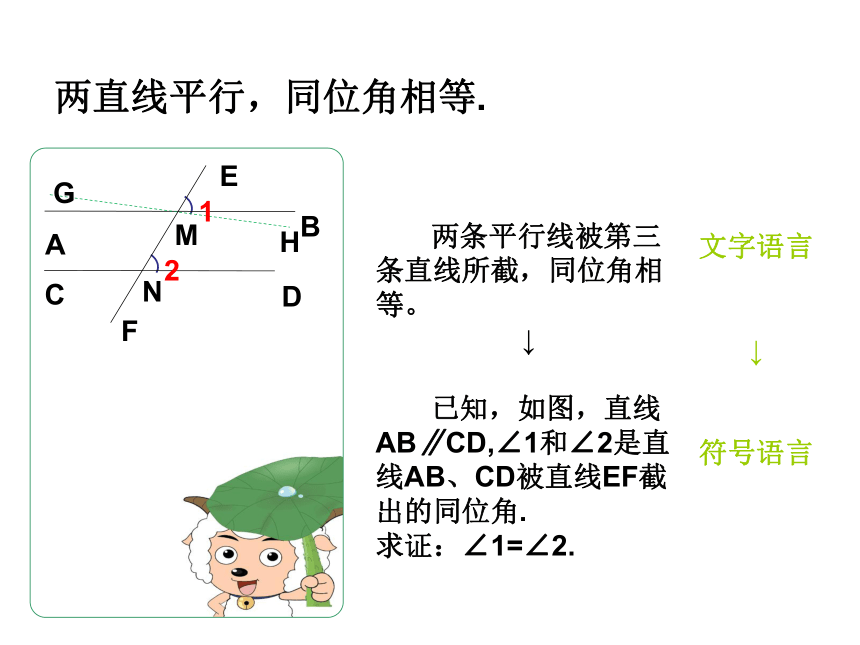
已知,如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.文字语言
↓
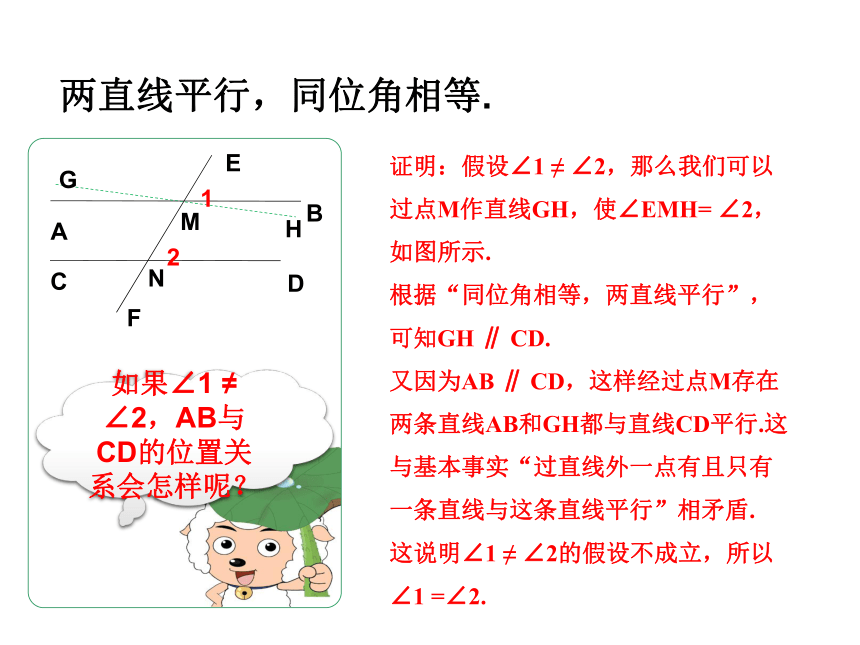
符号语言证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.两直线平行,同位角相等.如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢? 根据“两条平行线被第三条直线所截,内错角相等”.你能作出相关的图形吗?你能说说证明的思路吗? 你能根据所作的图形写出已知、求证吗?平行线的性质已知两直线平行,同位角相等,证明内错角相等两条平行线被第三条直线所截,内错角相等。
↓
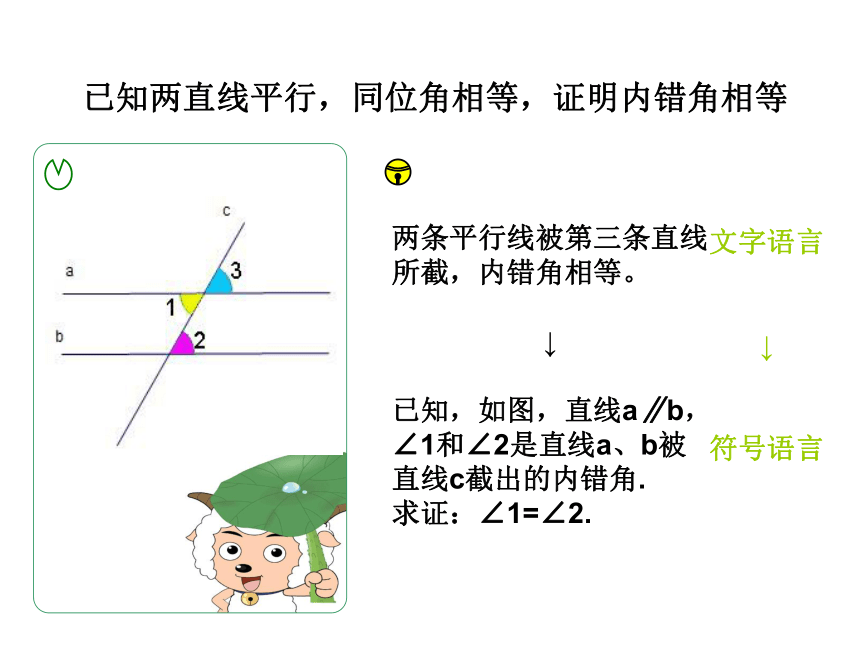
已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.
文字语言
↓
符号语言已知两直线平行,同位角相等,证明内错角相等.已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.你能说说证明的思路吗? 证明:∵a∥b(已知)
∴ ∠3=∠2
(两直线平行,同位角相等)
∵ ∠1=∠3(对顶角相等)
∴ ∠1=∠2(等量代换)反思:通过证明证实了这个命题是真命题,我们可以把它称为定理.即平行线的性质定理.这样就可以把它作为今后证明的依据.做一做:证明两直线平行,同旁内角互补作出相关的图形证明的思路根据所作的图形写出已知、求证已知两直线平行,同位角相等,证明同旁内角互补两条平行线被第三条直线所截,同旁内角互补。
↓
已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的同旁内角.
求证:∠1+∠2=180°
文字语言
↓
符号语言已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证明:∵a∥b(已知)
∴∠3=∠2
(两直线平行,同位角相等)
∵∠1+∠3=180°
(1平角=180°)
∴∠1+∠2=180°(等量代换)反思:通过推理的过程得证这个命题“两条平行线被第三条直线所截,同旁内角互补”是真命题.我们把它称为定理,即直线平行的性质定理,以后可以直接应用它来证明其他的结论.已知两直线平行,同位角相等,证明同旁内角互补例1 已知:如图,b∥a,c ∥a,∠1 ,∠2, ∠3是直线a,b,c被直线d截出的同位角.
求证: b∥c.证明: ∵b ∥a(已知)
∴ ∠2= ∠1(两直线平行,同位角相等)
∵c ∥a(已知)
∴ ∠3= ∠1(两直线平行,同位角相等)
∴ ∠2= ∠3(等量代换)
∴ b∥c(同位角相等,两直线平行)定理:平行于同一条直线的两条直线平行.归纳总结:证明命题的一般步骤根据题意
画出图形根据条件、结论,结合图形,写出已知、求证.经过分析,找出由已知推出求证的途径,写出证明过程先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的内容在图上标出符号,以便于叙述或推理过程的表达.分析的过程不要求写出来,有些题目中,已经画出了图形,写好了已知、求证,这时只要写出“证明”一项就可以了把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.第一步第二步第三步1.证明邻补角的平分线互相垂直. 已知:如图,∠AOB、∠BOC互为邻补角,
OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
证明: ∵OE平分∠AOB.
OF平分∠BOC(已知)
∴ ∠EOB=∠AOB
∠BOF=∠BOC(角平分线定义)
∵ ∠AOB+∠BOC=180°(1平角=180°)
∴ ∠EOB+∠BOF=(∠AOB+∠BOC)=90°(等式的性质)
即∠EOF=90°
∴ OE⊥OF(垂直的定义)小结 这节课我们主要研究了平行线的性质定理的证明,总结归纳了证明的一般步骤.
1.平行线的性质:
公理:两直线平行,同位角相等
定理:两直线平行,内错角相等
定理:两直线平行,同旁内角互补证明的一般步骤:活动与探究活动与探究活动与探究作业课本P177 课后作业
(一)随堂练习,习题7.5
(二)1.预习内容P178~178
2.预习提纲
(1)三角形的内角和定理是什么?
(2)三角形的内角和定理的证明.
↓
已知,如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.文字语言
↓
符号语言证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.两直线平行,同位角相等.如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢? 根据“两条平行线被第三条直线所截,内错角相等”.你能作出相关的图形吗?你能说说证明的思路吗? 你能根据所作的图形写出已知、求证吗?平行线的性质已知两直线平行,同位角相等,证明内错角相等两条平行线被第三条直线所截,内错角相等。
↓
已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.
文字语言
↓
符号语言已知两直线平行,同位角相等,证明内错角相等.已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.你能说说证明的思路吗? 证明:∵a∥b(已知)
∴ ∠3=∠2
(两直线平行,同位角相等)
∵ ∠1=∠3(对顶角相等)
∴ ∠1=∠2(等量代换)反思:通过证明证实了这个命题是真命题,我们可以把它称为定理.即平行线的性质定理.这样就可以把它作为今后证明的依据.做一做:证明两直线平行,同旁内角互补作出相关的图形证明的思路根据所作的图形写出已知、求证已知两直线平行,同位角相等,证明同旁内角互补两条平行线被第三条直线所截,同旁内角互补。
↓
已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的同旁内角.
求证:∠1+∠2=180°
文字语言
↓
符号语言已知,如图,直线a∥b,∠1和∠2是直线a、b被直线c截出的同旁内角.
求证:∠1+∠2=180°
证明:∵a∥b(已知)
∴∠3=∠2
(两直线平行,同位角相等)
∵∠1+∠3=180°
(1平角=180°)
∴∠1+∠2=180°(等量代换)反思:通过推理的过程得证这个命题“两条平行线被第三条直线所截,同旁内角互补”是真命题.我们把它称为定理,即直线平行的性质定理,以后可以直接应用它来证明其他的结论.已知两直线平行,同位角相等,证明同旁内角互补例1 已知:如图,b∥a,c ∥a,∠1 ,∠2, ∠3是直线a,b,c被直线d截出的同位角.
求证: b∥c.证明: ∵b ∥a(已知)
∴ ∠2= ∠1(两直线平行,同位角相等)
∵c ∥a(已知)
∴ ∠3= ∠1(两直线平行,同位角相等)
∴ ∠2= ∠3(等量代换)
∴ b∥c(同位角相等,两直线平行)定理:平行于同一条直线的两条直线平行.归纳总结:证明命题的一般步骤根据题意
画出图形根据条件、结论,结合图形,写出已知、求证.经过分析,找出由已知推出求证的途径,写出证明过程先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的内容在图上标出符号,以便于叙述或推理过程的表达.分析的过程不要求写出来,有些题目中,已经画出了图形,写好了已知、求证,这时只要写出“证明”一项就可以了把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.第一步第二步第三步1.证明邻补角的平分线互相垂直. 已知:如图,∠AOB、∠BOC互为邻补角,
OE平分∠AOB,OF平分∠BOC.
求证:OE⊥OF.
证明: ∵OE平分∠AOB.
OF平分∠BOC(已知)
∴ ∠EOB=∠AOB
∠BOF=∠BOC(角平分线定义)
∵ ∠AOB+∠BOC=180°(1平角=180°)
∴ ∠EOB+∠BOF=(∠AOB+∠BOC)=90°(等式的性质)
即∠EOF=90°
∴ OE⊥OF(垂直的定义)小结 这节课我们主要研究了平行线的性质定理的证明,总结归纳了证明的一般步骤.
1.平行线的性质:
公理:两直线平行,同位角相等
定理:两直线平行,内错角相等
定理:两直线平行,同旁内角互补证明的一般步骤:活动与探究活动与探究活动与探究作业课本P177 课后作业
(一)随堂练习,习题7.5
(二)1.预习内容P178~178
2.预习提纲
(1)三角形的内角和定理是什么?
(2)三角形的内角和定理的证明.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
