22.1.2 二次函数y=ax2的图象课件
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 386.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 00:00:00 | ||
图片预览


文档简介
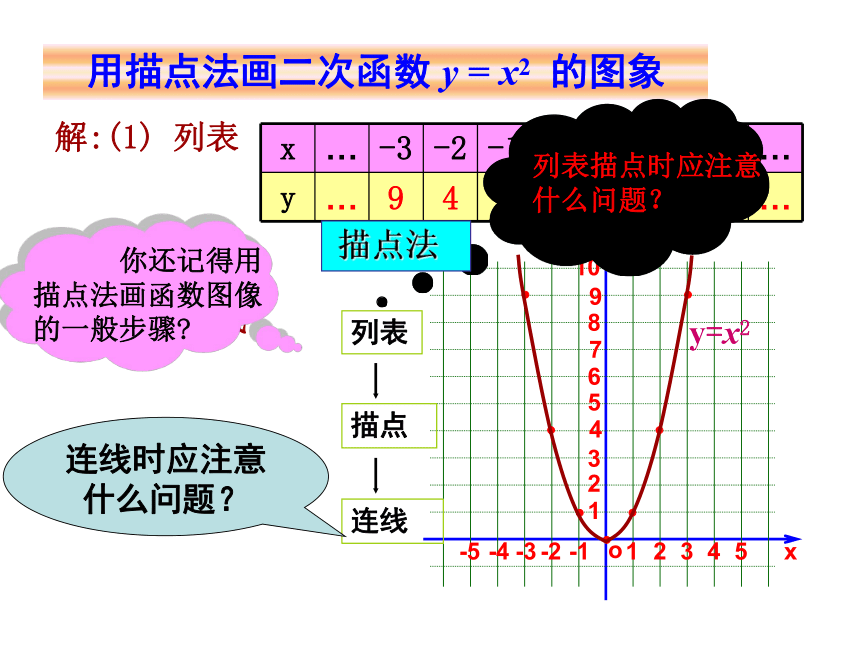
课件14张PPT。22.1.2二次函数y= ax2 的图象知识回顾1、二次函数的一般形式是怎样的?y=ax2+bx+c(a,b,c是常数,a≠ 0)解:(1) 列表(2) 描点(3) 连线y=x2用描点法画二次函数 y = x2 的图象列表描点时应注意
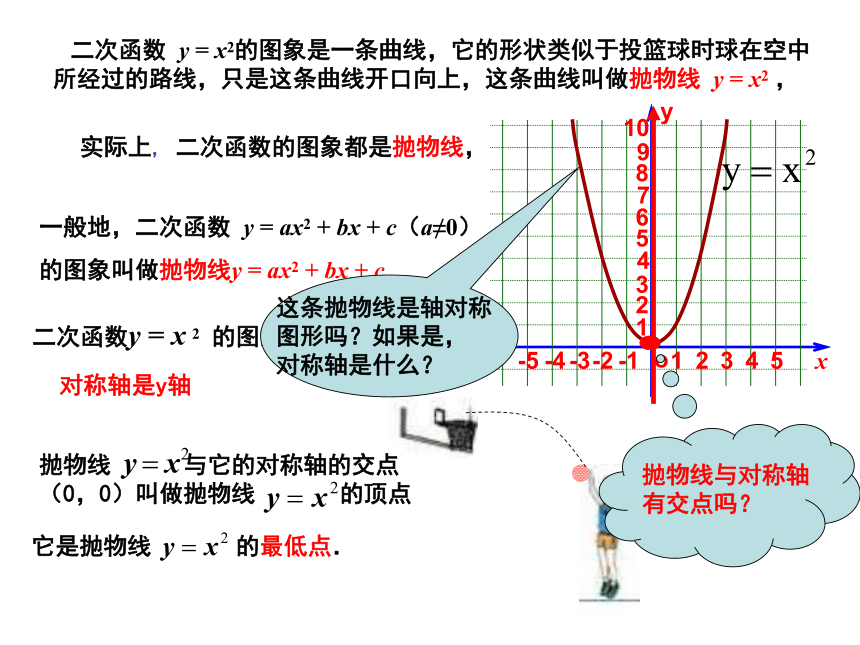
什么问题? 描点法列表描点连线连线时应注意什么问题? 二次函数 y = x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 ,二次函数y = x 2 的图象是轴对称图形,
一般地,二次函数 y = ax2 + bx + c(a≠0)
的图象叫做抛物线y = ax2 + bx + c抛物线 与它的对称轴的交点
(0,0)叫做抛物线 的顶点它是抛物线 的最低点.
实际上, 二次函数的图象都是抛物线,对称轴是y轴这条抛物线是轴对称
图形吗?如果是,
对称轴是什么?抛物线与对称轴
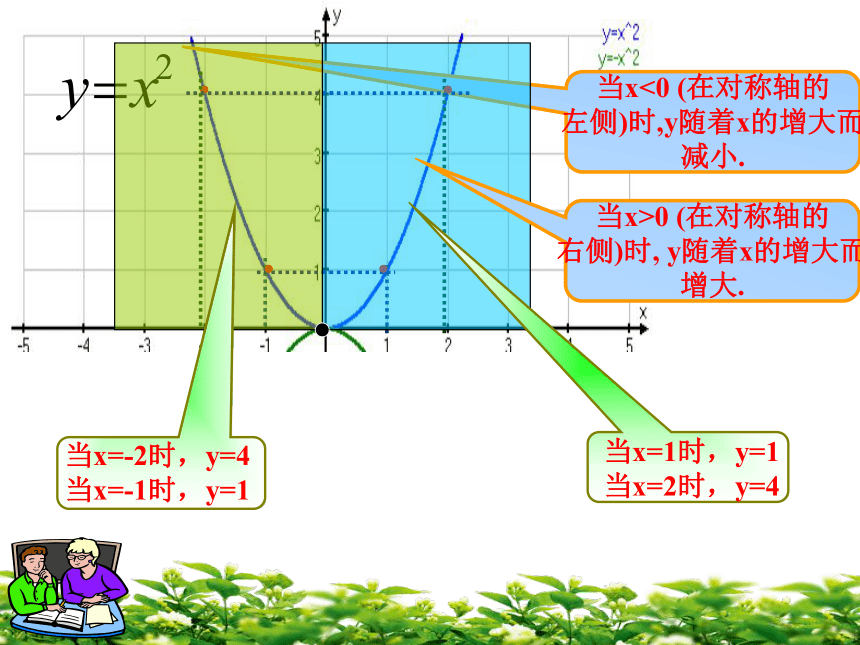
有交点吗?当x<0 (在对称轴的
左侧)时,y随着x的增大而
减小. 当x>0 (在对称轴的
右侧)时, y随着x的增大而
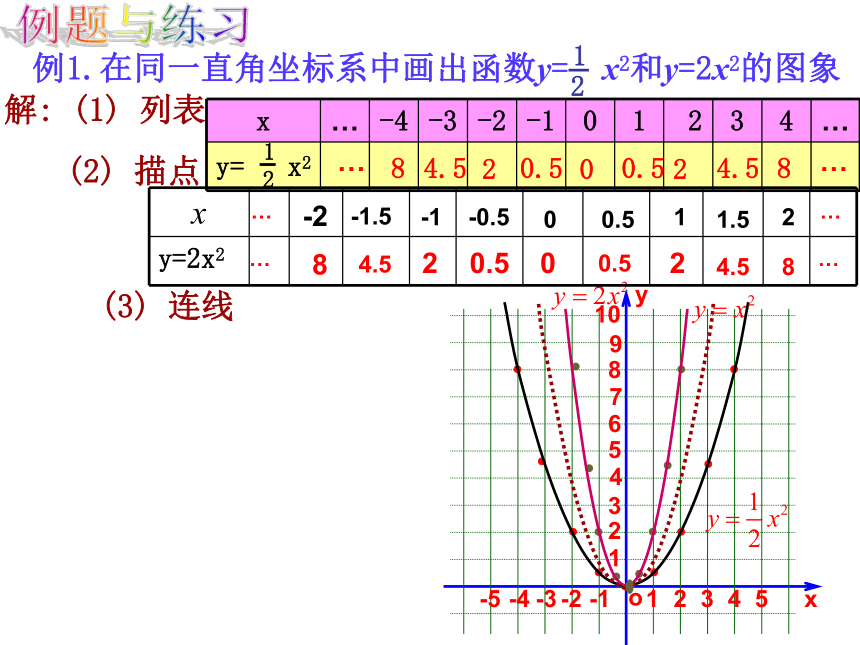
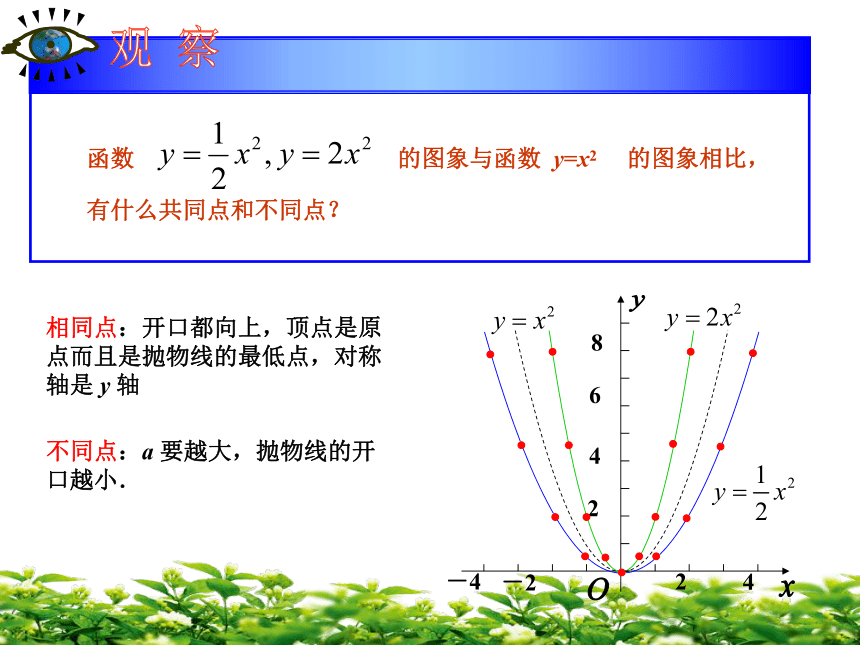
增大. 例题与练习例1.在同一直角坐标系中画出函数y= x2和y=2x2的图象解: (1) 列表(2) 描点(3) 连线8…20.500.524.58…4.58…………-2-1.5-1-0.500.511.524.520.500.524.58函数 的图象与函数 y=x2 的图象相比,有什么共同点和不同点?相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴不同点:a 要越大,抛物线的开口越小.向上向下(0 ,0)(0 ,0)y轴y轴当x<0时,
y随着x的增大而减小。
当x<0时,
y随着x的增大而增大。
x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,
归纳小结当x>0时,
y随着x的增大而增大。当x>0时,
y随着x的增大而减小。抛物线的开口就越小. |a|越小,抛物线的开口就越大.课堂练习1、函数y=4x2的图象的开口 ,对称轴
是 ,顶点是 ; 2、函数y=-3x2的图象的开口 ,对称轴是 , 顶点是 ___ 向上向下y轴 (0,0)(0,0)耐心填一填;y轴3、抛物线y=2x2的顶点坐标是 ,
对称轴是 ,
在 侧,y随着x的增大而增大;
在 侧 ,y随着x的增大而减小,
当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。 4、抛物线 在x轴的 方(除顶点外),
当 x〈 0 时,y随着x的 ;
当 x 〉0 时,y随着x的 ,
当 x = 0 时,函数y的值最大,最大值是 。
(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小01、二次函数y=ax2的图象是什么?2、二次函数y=ax2的图象有何性质?3、抛物线y=ax2 与y=-ax2有何关系?小结 作 业2、函数y= -0.2x2的图象的开口 ,
对称轴是__ _,顶点是 ;
1、函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;
再见
什么问题? 描点法列表描点连线连线时应注意什么问题? 二次函数 y = x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 ,二次函数y = x 2 的图象是轴对称图形,
一般地,二次函数 y = ax2 + bx + c(a≠0)
的图象叫做抛物线y = ax2 + bx + c抛物线 与它的对称轴的交点
(0,0)叫做抛物线 的顶点它是抛物线 的最低点.
实际上, 二次函数的图象都是抛物线,对称轴是y轴这条抛物线是轴对称
图形吗?如果是,
对称轴是什么?抛物线与对称轴
有交点吗?当x<0 (在对称轴的
左侧)时,y随着x的增大而
减小. 当x>0 (在对称轴的
右侧)时, y随着x的增大而
增大. 例题与练习例1.在同一直角坐标系中画出函数y= x2和y=2x2的图象解: (1) 列表(2) 描点(3) 连线8…20.500.524.58…4.58…………-2-1.5-1-0.500.511.524.520.500.524.58函数 的图象与函数 y=x2 的图象相比,有什么共同点和不同点?相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴不同点:a 要越大,抛物线的开口越小.向上向下(0 ,0)(0 ,0)y轴y轴当x<0时,
y随着x的增大而减小。
当x<0时,
y随着x的增大而增大。
x=0时,y最小=0x=0时,y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的,一般说来, |a|越大,
归纳小结当x>0时,
y随着x的增大而增大。当x>0时,
y随着x的增大而减小。抛物线的开口就越小. |a|越小,抛物线的开口就越大.课堂练习1、函数y=4x2的图象的开口 ,对称轴
是 ,顶点是 ; 2、函数y=-3x2的图象的开口 ,对称轴是 , 顶点是 ___ 向上向下y轴 (0,0)(0,0)耐心填一填;y轴3、抛物线y=2x2的顶点坐标是 ,
对称轴是 ,
在 侧,y随着x的增大而增大;
在 侧 ,y随着x的增大而减小,
当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。 4、抛物线 在x轴的 方(除顶点外),
当 x〈 0 时,y随着x的 ;
当 x 〉0 时,y随着x的 ,
当 x = 0 时,函数y的值最大,最大值是 。
(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小01、二次函数y=ax2的图象是什么?2、二次函数y=ax2的图象有何性质?3、抛物线y=ax2 与y=-ax2有何关系?小结 作 业2、函数y= -0.2x2的图象的开口 ,
对称轴是__ _,顶点是 ;
1、函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;
再见
同课章节目录
