第25章概率复习课(课件)
图片预览











文档简介
课件36张PPT。第二十五章 概率复习课 不可能事件0 1随机事件 0 (1)必然事件:在一定条件下,________会发生的事件.
(2)不可能事件:在一定条件下,必然________发生的事件.
(3)确定性事件:在一定条件下,________事件和________事件统称确定性事件.
(4)随机事件:在一定条件下,可能________也可能________的事件.一定 不会 必然 不可能 发生 不发生 1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( )
A.必然事件 B.随机事件
C.确定事件 D.不可能事件 变式1.下列事件为必然事件的是 ( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
考点1 事件的分类BD返回┃考点清单┃考点1 事件的分类变式3.下列事件中,属于确定事件的个数是( )
⑴打开电视,正在播广告;
⑵投掷一枚普通的骰子,掷得的点数小于10;
⑶射击运动员射击一次,命中10环;
⑷在一个只装有红球的袋中摸出白球.
A.0 B.1 C.2 D.3
C变式2.一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球。则下列事件是必然事件的是( )
A.摸出的4个球中至少有一个球是白球
B.摸出的4个球中至少有一个球是黑球
C.摸出的4个球中至少有两个球是黑球
D.摸出的4个球中至少有两个球是白球
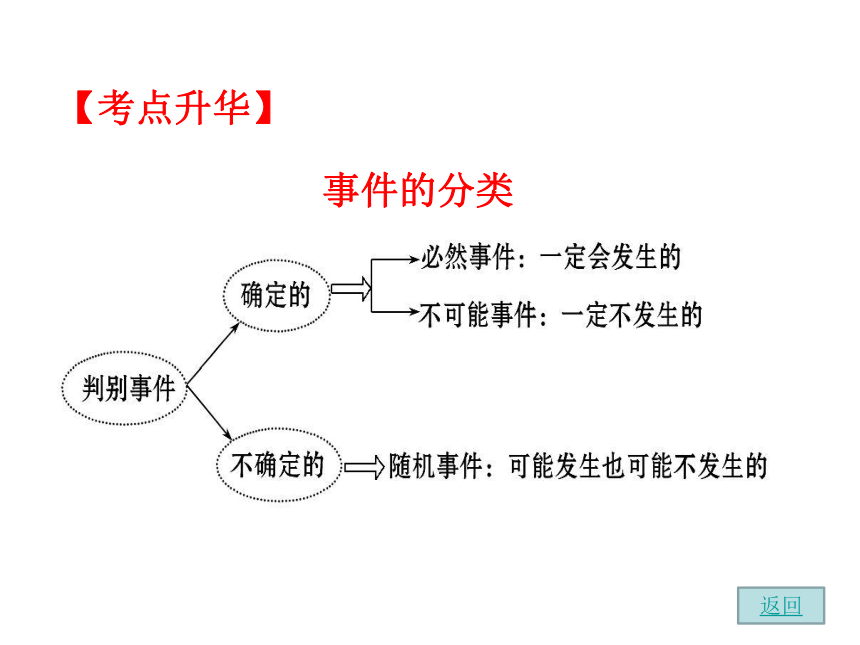
B┃考点清单┃【考点升华】
事件的分类返回1.世界杯足球赛正在巴西如火如荼地进行.赛前有人预测,巴西国家队夺冠的概率是90%.对他的说法理解正确的是( )
A.巴西队一定会夺冠
B.巴西队一定不会夺冠
C.巴西队夺冠的可能性很大
D.巴西队夺冠的可能性很小考点2 概率的意义C概率的定义:刻画随机事件A发生的可能性的大小的数值,称为随机事件A发生的概率.通常用字母P表示.┃考点清单┃变式.“兰州市明天降水概率是30%”,对此消息下列说法中正确的是( )
A.兰州市明天将有30%的地区降水
B.兰州市明天将有30%的时间降水
C.兰州市明天降水的可能性较小
D.兰州市明天肯定不降水
C【考点升华】
概率的意义返回1.若概率为02. 概率是指随机事件A发生的可能性的大小的数值.第25章 概率考点3 概率的计算与应用1.概率的定义:刻画随机事件A发生的可能性的大小的数值,称为随机事件A发生的概率.通常用字母P表示.
2.概率的计算
(1)P(必然事件)=________;
(2)P(不可能事件)=________;1 0 ┃考点清单┃次数 第25章 概率列表法 树状图法 稳定 相等 考点3 概率的计算与应用┃考点清单┃第25章 概率考点3 概率的计算与应用1.在一个不透明的布袋中装有3个白球和5个红球,它们除了颜色不同外,其余均相同.从中随机摸出一个球,摸到红球的概率是( )
┃考点清单┃DA变式1.已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )
A.1 B.2 C.3 D.4第25章 概率考点3 概率的计算与应用┃考点清单┃D变式2.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他均相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.16个 B.15个
C.13个 D.12个第25章 概率考点3 概率的计算与应用┃考点清单┃2.如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )A . B. C. D.A变式1.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
A. B. C. D.
D第25章 概率考点3 概率的计算与应用3.在一个口袋中有4个完全相同的小球,把它们分别标号为①,②,③,④,随机地摸出一个小球,记录后放回,再随机摸出一个小球,则两次摸出的小球的标号相同的概率是( )
A. B. C. D.
┃考点清单┃C列表法 第25章 概率考点3 概率的计算与应用┃考点清单┃变式1.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .列表法 第25章 概率考点3 概率的计算与应用变式2.[2014·玉林] 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A. B. C. D.
┃考点清单┃C∴一共有12种情况,符合条件的有2种,即列表法 第25章 概率考点3 概率的计算与应用┃考点清单┃∴一共有6种情况,符合条件的有4种,即 P=列表法 变式3.第45届世界体操锦标赛于2014年10月3日至12日在南宁市隆重举行,某校从小记者团内负责体育赛事报道的3名同学(2男1女)中任选2名前往采访,那么选出的2名同学恰好是一男一女的概率是________.4.[2013·柳州] 韦玲和覃静两人玩“剪刀、石头、布”的游戏,游戏规则为:剪刀胜布,布胜石头,石头胜剪刀.
(1)请用列表法或树状图表示出所有可能出现的游戏结果;
(2)求韦玲胜出的概率.┃考点清单┃考点3 概率的计算与应用(2)∵韦玲胜出的可能结果有3种,
故韦玲胜出的概率为 .
第25章 概率5.甲、乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一个球,标号是1的概率;
(2)从袋中随机摸出一个球然后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数,则甲胜;若两次摸出的球的标号之和为奇数,则乙胜.试分析这个游戏公平吗?请说明理由.┃考点清单┃考点3 概率的计算与应用第25章 概率考点3 概率的计算与应用┃考点清单┃【考点升华】 概率的计算与应用
求随机事件概率的类型及策略
1.有限等可能性事件:
(1)事件只包含一个因素:用列举的方法,根据公式P= 求得结果.
(2)事件包含两个因素:用列表或画树状图的方法,根据公式P= 求得结果.
(3)事件包含三个因素:用画树状图的方法,根据公式P= 求得结果.
2.无限等可能性事件:与面积有关的事件的概率可以通过区域面积与总面积的比值来求解.【考点升华】概率的计算与应用
关于游戏中概率的两个注意点
1.判断游戏公平的标准:
游戏双方获胜的概率(或游戏得分)是否相等,是判断游戏是否公平的唯一标准;若相等,则游戏公平,若不相等,则游戏不公平.
2.变非公平游戏为公平游戏的两个途径:
(1)改变游戏规则,使双方获胜的概率相等.
(2)不改变双方获胜的概率,改变得分情况,使双方得分相等.返回1.[2014?桂林] 初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的统计图.
(1)这次调查的家长总人数为________人,表示“无所谓”的家长人数为________人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是________;200 40 ┃考点清单┃考点4 统计与概率的结合(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.返回 (1)这节课复习了什么知识?
(2)你学到了哪些思考问题的方法?
(3)用了什么数学思想方法解决问题?4.小结5.布置作业 单元双测P49--50第25章 概率┃拓展互动探究┃? 类型之一 事件的分类类型题展示例1 [2013?沈阳] 下列事件中,是不可能事件的是( )
A.买一张电影票,座位号是奇数
B.射击运动员射击一次,命中9环
C.明天会下雨
D.度量三角形的内角和,结果是360°第25章 概率变式题1 [2014?梅州] 下列事件中是必然事件的是( )
A.明天太阳从西边升起
B.篮球队员在罚球线上投篮一次,未投中
C.实心铁球投入水中会沉入水底
D.抛出一枚硬币,落地后正面朝上C 第25章 概率变式题2 [2013?衡阳] “a是实数,|a|≥0”是( )
A.必然事件 B.不确定事件
C.不可能事件 D.随机事件A 第25章 概率? 类型之二 概率的定义[答案] D第25章 概率变式题1 [2014?厦门] 一个圆形转盘被平均分成红、黄、蓝、白4个扇形区域,向其投掷一枚飞镖,飞镖落在转盘上,则飞镖落在黄色区域的概率是________.
变式题2 [2014?珠海] 桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,现在从桶里随机摸出-个球,则摸到白球的概率为________.
变式题3 [2014?河南] 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球.两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是________.第25章 概率? 类型之三 概率的计算和应用[答案] D第25章 概率[考点] 列表法或树状图法.第25章 概率1.[2013·贺州] 甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树状图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.第25章 概率第25章 概率2.有两个构造完全相同(除所标数字外)的转盘A,B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?图8-35-9第25章 概率
(2)不可能事件:在一定条件下,必然________发生的事件.
(3)确定性事件:在一定条件下,________事件和________事件统称确定性事件.
(4)随机事件:在一定条件下,可能________也可能________的事件.一定 不会 必然 不可能 发生 不发生 1.“抛一枚均匀硬币,落地后正面朝上”这一事件是( )
A.必然事件 B.随机事件
C.确定事件 D.不可能事件 变式1.下列事件为必然事件的是 ( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
考点1 事件的分类BD返回┃考点清单┃考点1 事件的分类变式3.下列事件中,属于确定事件的个数是( )
⑴打开电视,正在播广告;
⑵投掷一枚普通的骰子,掷得的点数小于10;
⑶射击运动员射击一次,命中10环;
⑷在一个只装有红球的袋中摸出白球.
A.0 B.1 C.2 D.3
C变式2.一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球。则下列事件是必然事件的是( )
A.摸出的4个球中至少有一个球是白球
B.摸出的4个球中至少有一个球是黑球
C.摸出的4个球中至少有两个球是黑球
D.摸出的4个球中至少有两个球是白球
B┃考点清单┃【考点升华】
事件的分类返回1.世界杯足球赛正在巴西如火如荼地进行.赛前有人预测,巴西国家队夺冠的概率是90%.对他的说法理解正确的是( )
A.巴西队一定会夺冠
B.巴西队一定不会夺冠
C.巴西队夺冠的可能性很大
D.巴西队夺冠的可能性很小考点2 概率的意义C概率的定义:刻画随机事件A发生的可能性的大小的数值,称为随机事件A发生的概率.通常用字母P表示.┃考点清单┃变式.“兰州市明天降水概率是30%”,对此消息下列说法中正确的是( )
A.兰州市明天将有30%的地区降水
B.兰州市明天将有30%的时间降水
C.兰州市明天降水的可能性较小
D.兰州市明天肯定不降水
C【考点升华】
概率的意义返回1.若概率为0
2.概率的计算
(1)P(必然事件)=________;
(2)P(不可能事件)=________;1 0 ┃考点清单┃次数 第25章 概率列表法 树状图法 稳定 相等 考点3 概率的计算与应用┃考点清单┃第25章 概率考点3 概率的计算与应用1.在一个不透明的布袋中装有3个白球和5个红球,它们除了颜色不同外,其余均相同.从中随机摸出一个球,摸到红球的概率是( )
┃考点清单┃DA变式1.已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )
A.1 B.2 C.3 D.4第25章 概率考点3 概率的计算与应用┃考点清单┃D变式2.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他均相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.16个 B.15个
C.13个 D.12个第25章 概率考点3 概率的计算与应用┃考点清单┃2.如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )A . B. C. D.A变式1.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是( )
A. B. C. D.
D第25章 概率考点3 概率的计算与应用3.在一个口袋中有4个完全相同的小球,把它们分别标号为①,②,③,④,随机地摸出一个小球,记录后放回,再随机摸出一个小球,则两次摸出的小球的标号相同的概率是( )
A. B. C. D.
┃考点清单┃C列表法 第25章 概率考点3 概率的计算与应用┃考点清单┃变式1.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .列表法 第25章 概率考点3 概率的计算与应用变式2.[2014·玉林] 一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( )
A. B. C. D.
┃考点清单┃C∴一共有12种情况,符合条件的有2种,即列表法 第25章 概率考点3 概率的计算与应用┃考点清单┃∴一共有6种情况,符合条件的有4种,即 P=列表法 变式3.第45届世界体操锦标赛于2014年10月3日至12日在南宁市隆重举行,某校从小记者团内负责体育赛事报道的3名同学(2男1女)中任选2名前往采访,那么选出的2名同学恰好是一男一女的概率是________.4.[2013·柳州] 韦玲和覃静两人玩“剪刀、石头、布”的游戏,游戏规则为:剪刀胜布,布胜石头,石头胜剪刀.
(1)请用列表法或树状图表示出所有可能出现的游戏结果;
(2)求韦玲胜出的概率.┃考点清单┃考点3 概率的计算与应用(2)∵韦玲胜出的可能结果有3种,
故韦玲胜出的概率为 .
第25章 概率5.甲、乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一个球,标号是1的概率;
(2)从袋中随机摸出一个球然后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数,则甲胜;若两次摸出的球的标号之和为奇数,则乙胜.试分析这个游戏公平吗?请说明理由.┃考点清单┃考点3 概率的计算与应用第25章 概率考点3 概率的计算与应用┃考点清单┃【考点升华】 概率的计算与应用
求随机事件概率的类型及策略
1.有限等可能性事件:
(1)事件只包含一个因素:用列举的方法,根据公式P= 求得结果.
(2)事件包含两个因素:用列表或画树状图的方法,根据公式P= 求得结果.
(3)事件包含三个因素:用画树状图的方法,根据公式P= 求得结果.
2.无限等可能性事件:与面积有关的事件的概率可以通过区域面积与总面积的比值来求解.【考点升华】概率的计算与应用
关于游戏中概率的两个注意点
1.判断游戏公平的标准:
游戏双方获胜的概率(或游戏得分)是否相等,是判断游戏是否公平的唯一标准;若相等,则游戏公平,若不相等,则游戏不公平.
2.变非公平游戏为公平游戏的两个途径:
(1)改变游戏规则,使双方获胜的概率相等.
(2)不改变双方获胜的概率,改变得分情况,使双方得分相等.返回1.[2014?桂林] 初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的统计图.
(1)这次调查的家长总人数为________人,表示“无所谓”的家长人数为________人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是________;200 40 ┃考点清单┃考点4 统计与概率的结合(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.返回 (1)这节课复习了什么知识?
(2)你学到了哪些思考问题的方法?
(3)用了什么数学思想方法解决问题?4.小结5.布置作业 单元双测P49--50第25章 概率┃拓展互动探究┃? 类型之一 事件的分类类型题展示例1 [2013?沈阳] 下列事件中,是不可能事件的是( )
A.买一张电影票,座位号是奇数
B.射击运动员射击一次,命中9环
C.明天会下雨
D.度量三角形的内角和,结果是360°第25章 概率变式题1 [2014?梅州] 下列事件中是必然事件的是( )
A.明天太阳从西边升起
B.篮球队员在罚球线上投篮一次,未投中
C.实心铁球投入水中会沉入水底
D.抛出一枚硬币,落地后正面朝上C 第25章 概率变式题2 [2013?衡阳] “a是实数,|a|≥0”是( )
A.必然事件 B.不确定事件
C.不可能事件 D.随机事件A 第25章 概率? 类型之二 概率的定义[答案] D第25章 概率变式题1 [2014?厦门] 一个圆形转盘被平均分成红、黄、蓝、白4个扇形区域,向其投掷一枚飞镖,飞镖落在转盘上,则飞镖落在黄色区域的概率是________.
变式题2 [2014?珠海] 桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,现在从桶里随机摸出-个球,则摸到白球的概率为________.
变式题3 [2014?河南] 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球.两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是________.第25章 概率? 类型之三 概率的计算和应用[答案] D第25章 概率[考点] 列表法或树状图法.第25章 概率1.[2013·贺州] 甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树状图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.第25章 概率第25章 概率2.有两个构造完全相同(除所标数字外)的转盘A,B,游戏规定,转动两个转盘各一次,指向大的数字获胜.现由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?图8-35-9第25章 概率
同课章节目录
