1.1 周期现象 课件2
图片预览






文档简介
课件22张PPT。第一章 三角函数
1.1 周期现象实例1:日出日落、月缺月圆、寒来暑往……自然界中有许多“按一定规律周而复始”的现象,这种按一定规律不断重复出现的现象称为周期现象.
周期现象就是描述具有“周而复始”规律的现象.思考:多长时间重复出现一次?实例2:同学们,你们有没有见过大海,观看过潮涨潮落?相信大家见过的不多,那今天就来看看著名的钱塘江潮. 思考:潮汐是周期现象吗? 众所周知,海水会发生潮汐现象,大约在每一昼夜的时间里,潮水会涨落两次,因此潮汐是周期现象. 另外,我们发现钟表上的时针、分针和秒针每经过一周就会重复,这也是一种周期现象. 那么,我们这节课要研究的主要内容就是周期现象.了解周期现象在现实中的广泛存在;(重点)
经历数据分析及观察散点图特征,感受周期现象对实际工作的意义;(重点)
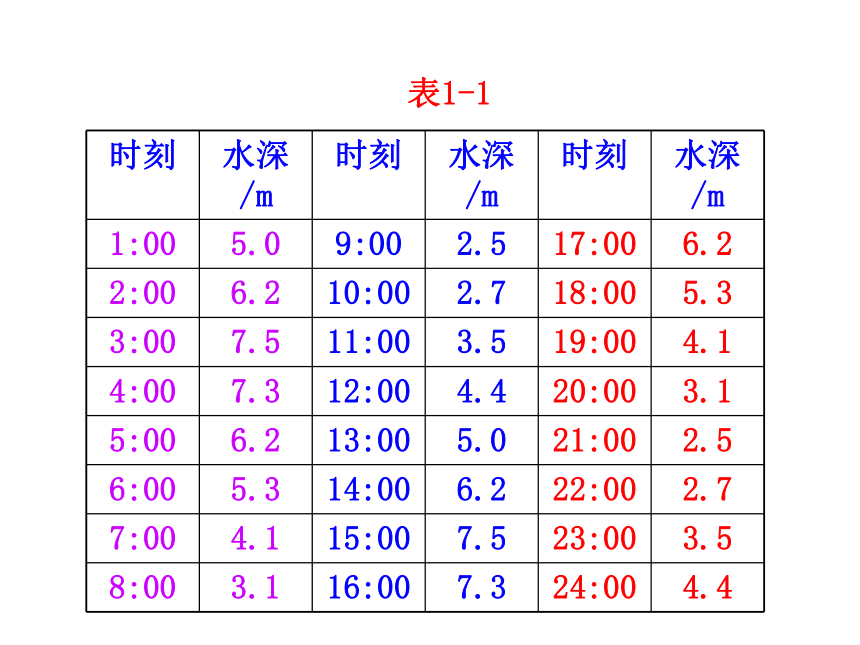
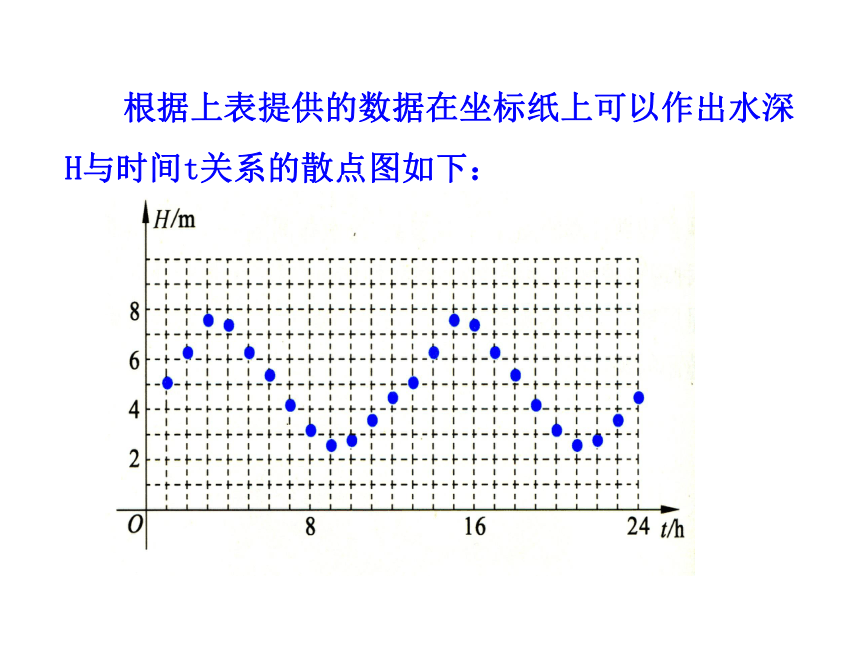
3.能熟练地判断简单的实际问题的周期.(难点)探究点1 对周期现象的理解 当潮汐发生时,水的深度会产生周期性变化,为了研究水深的变化规律,我们可以构造一个函数.例如,确定一个位置,考察该处水深H和时间t的关系,那么H就是t的函数.下表1-1是某港口在某一天水深与时间的对应关系表,通过表中数据,我们来研究H(t)这个函数.表1-1 根据上表提供的数据在坐标纸上可以作出水深H与时间t关系的散点图如下: 思考:上述现象是周期现象吗?
提示:从散点图可以看出,每经过相同的时间间隔T(12h),水深度就重复出现相同的数值,因此,水深是周期性变化的.问题1:你能否举出生活中的几个周期现象?
提示:钟摆的摆动、地球公转、交通路口的红绿灯
变化、城市里霓虹灯的闪烁变幻等.
问题2:判断周期现象能不能只判定该现象只要重复出现就可以?
提示:不可以,因为周期现象必须是间隔相同的时间重复出现.提升总结:周期现象以及周期现象的判断
1.周期现象指的是每间隔相同时间会重复出现的现象.
2.判断周期现象时要把握好两点:
(1)会重复出现.
(2)要间隔的时间相同.这两点缺一不可.探究点2 周期现象的实际举例例1.地球围绕着太阳转(如图),地球到太阳的距离y随时间的变化是周期性的吗?解: 根据物理学知识,我们知道在任何一个确定的时刻,地球与太阳的距离y是唯一确定的,每经过一年地球围绕着太阳转一周.无论从哪个时刻t算起,经过一年时间,地球又回到原来的位置,所以,地球与太阳的距离是周期变化的. 例2.如图是钟摆的示意图,摆心A到铅垂线MN的距离记为y,钟摆偏离铅垂线MN的角记为θ,根据物理知识,y与θ都随时间的变化而周期性变化. 例3. 如图是水车的示意图.水车上点P到水面的距离为y.假设水车5 min转一圈,那么y的值每经过5 min就会重复出现,因此,距离y随时间的变化规律也具有周期性. 1. 由上面的例子,我们可以看到在自然界中存在着丰富的周期现象.总结 2.当我们用周期性描述周期现象时,会出现不同的自变量,有一些例子以时间为自变量,有一些例子以角度为自变量.1.地球上一年春、夏、秋、冬四季的变化是周期现象吗?2.钟表的分针每小时转一圈,它的运行是周期现象吗?3.连续抛一枚硬币,面值朝上我们记为 0 ,面值朝下我们记为 1 ,数字 0 和 1 是否会周期性地重复出现?
4.地球同步卫星绕地球公转是周期现象吗?是是否是1.下列现象是周期现象的序号是_______.
①鸡季节性的换毛现象;
②一季度某品牌汽车的销售量;
③经一路某路口的红绿灯每30秒转换一次;
④奥运会每四年举办一次.①③④2.2012年第30届奥运会在英国伦敦举行,而第14届
奥运会也是在此举行的,那么第14届奥运会举行的
年份是( )
A.1944年 B.1908年 C.1948年 D.1952年
提示:奥运会每4年举行一届,第14届和第30届相差16届,即相差64年,因此第14 届奥运会举行的年份是1948年.C3.今天是星期三,那么7k(k∈Z)天后的那一天是星期几?7k(k∈Z)天前的那一天是星期几?100天后的那一天是星期几?答案: 星期三 星期三 星期五 知道了周期现象在现实中广泛存在.
感受到了周期现象对实际工作的意义.
3.能判断简单的实际问题的周期.回顾本节课的收获惟有埋头,才能出头,急于出人头地,除了自寻苦恼之外,不会真正得到什么.
——莎翁
1.1 周期现象实例1:日出日落、月缺月圆、寒来暑往……自然界中有许多“按一定规律周而复始”的现象,这种按一定规律不断重复出现的现象称为周期现象.
周期现象就是描述具有“周而复始”规律的现象.思考:多长时间重复出现一次?实例2:同学们,你们有没有见过大海,观看过潮涨潮落?相信大家见过的不多,那今天就来看看著名的钱塘江潮. 思考:潮汐是周期现象吗? 众所周知,海水会发生潮汐现象,大约在每一昼夜的时间里,潮水会涨落两次,因此潮汐是周期现象. 另外,我们发现钟表上的时针、分针和秒针每经过一周就会重复,这也是一种周期现象. 那么,我们这节课要研究的主要内容就是周期现象.了解周期现象在现实中的广泛存在;(重点)
经历数据分析及观察散点图特征,感受周期现象对实际工作的意义;(重点)
3.能熟练地判断简单的实际问题的周期.(难点)探究点1 对周期现象的理解 当潮汐发生时,水的深度会产生周期性变化,为了研究水深的变化规律,我们可以构造一个函数.例如,确定一个位置,考察该处水深H和时间t的关系,那么H就是t的函数.下表1-1是某港口在某一天水深与时间的对应关系表,通过表中数据,我们来研究H(t)这个函数.表1-1 根据上表提供的数据在坐标纸上可以作出水深H与时间t关系的散点图如下: 思考:上述现象是周期现象吗?
提示:从散点图可以看出,每经过相同的时间间隔T(12h),水深度就重复出现相同的数值,因此,水深是周期性变化的.问题1:你能否举出生活中的几个周期现象?
提示:钟摆的摆动、地球公转、交通路口的红绿灯
变化、城市里霓虹灯的闪烁变幻等.
问题2:判断周期现象能不能只判定该现象只要重复出现就可以?
提示:不可以,因为周期现象必须是间隔相同的时间重复出现.提升总结:周期现象以及周期现象的判断
1.周期现象指的是每间隔相同时间会重复出现的现象.
2.判断周期现象时要把握好两点:
(1)会重复出现.
(2)要间隔的时间相同.这两点缺一不可.探究点2 周期现象的实际举例例1.地球围绕着太阳转(如图),地球到太阳的距离y随时间的变化是周期性的吗?解: 根据物理学知识,我们知道在任何一个确定的时刻,地球与太阳的距离y是唯一确定的,每经过一年地球围绕着太阳转一周.无论从哪个时刻t算起,经过一年时间,地球又回到原来的位置,所以,地球与太阳的距离是周期变化的. 例2.如图是钟摆的示意图,摆心A到铅垂线MN的距离记为y,钟摆偏离铅垂线MN的角记为θ,根据物理知识,y与θ都随时间的变化而周期性变化. 例3. 如图是水车的示意图.水车上点P到水面的距离为y.假设水车5 min转一圈,那么y的值每经过5 min就会重复出现,因此,距离y随时间的变化规律也具有周期性. 1. 由上面的例子,我们可以看到在自然界中存在着丰富的周期现象.总结 2.当我们用周期性描述周期现象时,会出现不同的自变量,有一些例子以时间为自变量,有一些例子以角度为自变量.1.地球上一年春、夏、秋、冬四季的变化是周期现象吗?2.钟表的分针每小时转一圈,它的运行是周期现象吗?3.连续抛一枚硬币,面值朝上我们记为 0 ,面值朝下我们记为 1 ,数字 0 和 1 是否会周期性地重复出现?
4.地球同步卫星绕地球公转是周期现象吗?是是否是1.下列现象是周期现象的序号是_______.
①鸡季节性的换毛现象;
②一季度某品牌汽车的销售量;
③经一路某路口的红绿灯每30秒转换一次;
④奥运会每四年举办一次.①③④2.2012年第30届奥运会在英国伦敦举行,而第14届
奥运会也是在此举行的,那么第14届奥运会举行的
年份是( )
A.1944年 B.1908年 C.1948年 D.1952年
提示:奥运会每4年举行一届,第14届和第30届相差16届,即相差64年,因此第14 届奥运会举行的年份是1948年.C3.今天是星期三,那么7k(k∈Z)天后的那一天是星期几?7k(k∈Z)天前的那一天是星期几?100天后的那一天是星期几?答案: 星期三 星期三 星期五 知道了周期现象在现实中广泛存在.
感受到了周期现象对实际工作的意义.
3.能判断简单的实际问题的周期.回顾本节课的收获惟有埋头,才能出头,急于出人头地,除了自寻苦恼之外,不会真正得到什么.
——莎翁
