1.2 角的概念的推广 课件1
图片预览






文档简介
课件19张PPT。第一章 三角函数1.2 角的概念的推广学习目标1、理解并掌握 “象限角”、“终边相同的角”的含义。
2、掌握所有与α角终边相同的角(包括α角)的表示方法。
3、体会运动变化观点,深刻理解推广后的角的概念。新课引入. 任意角的大小没有范围,研究起来很麻烦,
为了研究方便,我们往往在平面直角坐标系中来讨论角。新课引入在同一坐标系中,相等的角的终边有何关系? 终边相同的角有何关系?与30终边相同的角由哪些?探究点1 角的顶点重合于坐标原点,角的始边重合于x轴的非负半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角。
角的终边落在坐标轴上,则此角不属于任何一个象限。(坐标轴上的角 )
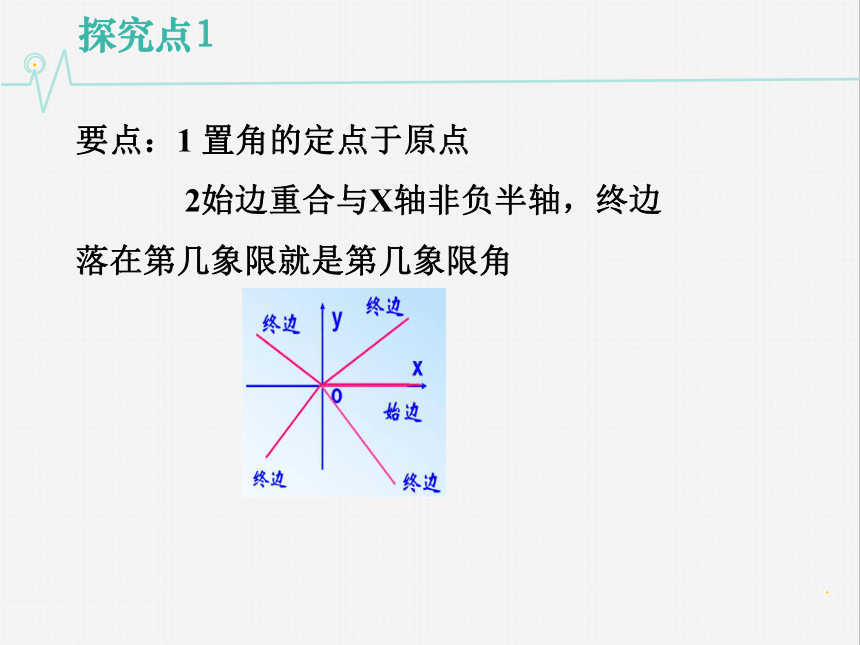
探究点1要点:1 置角的定点于原点
2始边重合与X轴非负半轴,终边落在第几象限就是第几象限角
探究点2如果角的终边落在了坐标轴上,就认为这个角不属于任何象限。例如:角的终边落在x轴或y轴上。已知α,β角的终边相同,那么α-β的终边在( C )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上典例精讲:题型一:探究点3典例精讲:题型二:终边落在x轴上的角的集合为( )
A.{β|β=n·360°,n∈Z}
B.{β|β=n·180°,n∈Z}
C.{β|β=(2n+1)·180°,n∈Z}
D.{β|β=(2n+1)·360°,n∈Z}
解析:终边落在x轴上,那么角的终边就落在180和360的终边上,表示出所有终边在这两个角终边上的角即可。
答案:B探究点4在0到360度内找与已知角终边相同的角,方法是:用所给角除以360。
所给角是正的:按通常的除法进行;
所给角是负的:角度除以360,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。探究点4与终边相同的角的一般形式要注意以下四点:
① k∈Z;
②是任意角;
③ k·360o与间是“+”号,如k·360o-30o,应看成k·360o+(-30o);
④ 终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360o的整数倍.探究点5判断一个角是第几象限角,方法是:
所给角改写成 :
+k ·360 ( K∈Z,0≤<360 )的形式,
在第几象限就是第几象限角典例精讲:题型三:拓展提升:题型三:根据角α终边的位置,写出角α 的集合
在第二象限角平分线上时,α=________,k∈Z;
在第一、三象限角平分线上时,α=________,k∈Z.
解析:先研究角在[0°,360°)内的情况,再加上360°的整数倍,即可得终边在第二象限角平分线上的角,α=135°+k·360°,k∈Z;终边在第一、三象限角平分线上,α=45°+k·180°,k∈Z.
答案:135°+k·360° 45°+k·180°课堂练习若角α满足α=45°+k·180°,k∈Z,则角α的终边 落在( )
A.第一或第三象限 B.第一或第二象限
C.第二或第四象限 D.第三或第四象限
解析:选A.当k为奇数时,角α与225°角终边相同,在第三象限;当k为偶数时,角α与45°角终边相同,在第一象限.课堂练习在0°~360°范围内,找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)549°;
(2)-60°;
(3)-503°36′课堂练习解:
(1)549°=189°+360°,而180°<189°<270°,因此549°角为第三象限角,且在0°~360°范围内,与189°角有相同的终边.
(2)-60°=300°-360°,而270°<300°<360°,因此-60°角为第四象限角,且在0°~360°范围内,与300°角有相同的终边.
(3)-503°36′=216°2 4′-2×360°,而180°<216°24′<270°,因此,-503°36′角是第三象限角,且在0°~360°范围内,与216°24′角有相同的终边.归纳小结任意角的概念:旋转方向、旋转量
象限角:定点、始边、终边的位置
终边与角相同的角:
2、掌握所有与α角终边相同的角(包括α角)的表示方法。
3、体会运动变化观点,深刻理解推广后的角的概念。新课引入. 任意角的大小没有范围,研究起来很麻烦,
为了研究方便,我们往往在平面直角坐标系中来讨论角。新课引入在同一坐标系中,相等的角的终边有何关系? 终边相同的角有何关系?与30终边相同的角由哪些?探究点1 角的顶点重合于坐标原点,角的始边重合于x轴的非负半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角。
角的终边落在坐标轴上,则此角不属于任何一个象限。(坐标轴上的角 )
探究点1要点:1 置角的定点于原点
2始边重合与X轴非负半轴,终边落在第几象限就是第几象限角
探究点2如果角的终边落在了坐标轴上,就认为这个角不属于任何象限。例如:角的终边落在x轴或y轴上。已知α,β角的终边相同,那么α-β的终边在( C )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上典例精讲:题型一:探究点3典例精讲:题型二:终边落在x轴上的角的集合为( )
A.{β|β=n·360°,n∈Z}
B.{β|β=n·180°,n∈Z}
C.{β|β=(2n+1)·180°,n∈Z}
D.{β|β=(2n+1)·360°,n∈Z}
解析:终边落在x轴上,那么角的终边就落在180和360的终边上,表示出所有终边在这两个角终边上的角即可。
答案:B探究点4在0到360度内找与已知角终边相同的角,方法是:用所给角除以360。
所给角是正的:按通常的除法进行;
所给角是负的:角度除以360,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。探究点4与终边相同的角的一般形式要注意以下四点:
① k∈Z;
②是任意角;
③ k·360o与间是“+”号,如k·360o-30o,应看成k·360o+(-30o);
④ 终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360o的整数倍.探究点5判断一个角是第几象限角,方法是:
所给角改写成 :
+k ·360 ( K∈Z,0≤<360 )的形式,
在第几象限就是第几象限角典例精讲:题型三:拓展提升:题型三:根据角α终边的位置,写出角α 的集合
在第二象限角平分线上时,α=________,k∈Z;
在第一、三象限角平分线上时,α=________,k∈Z.
解析:先研究角在[0°,360°)内的情况,再加上360°的整数倍,即可得终边在第二象限角平分线上的角,α=135°+k·360°,k∈Z;终边在第一、三象限角平分线上,α=45°+k·180°,k∈Z.
答案:135°+k·360° 45°+k·180°课堂练习若角α满足α=45°+k·180°,k∈Z,则角α的终边 落在( )
A.第一或第三象限 B.第一或第二象限
C.第二或第四象限 D.第三或第四象限
解析:选A.当k为奇数时,角α与225°角终边相同,在第三象限;当k为偶数时,角α与45°角终边相同,在第一象限.课堂练习在0°~360°范围内,找出与下列各角终边相同的角,并指出它们是第几象限角:
(1)549°;
(2)-60°;
(3)-503°36′课堂练习解:
(1)549°=189°+360°,而180°<189°<270°,因此549°角为第三象限角,且在0°~360°范围内,与189°角有相同的终边.
(2)-60°=300°-360°,而270°<300°<360°,因此-60°角为第四象限角,且在0°~360°范围内,与300°角有相同的终边.
(3)-503°36′=216°2 4′-2×360°,而180°<216°24′<270°,因此,-503°36′角是第三象限角,且在0°~360°范围内,与216°24′角有相同的终边.归纳小结任意角的概念:旋转方向、旋转量
象限角:定点、始边、终边的位置
终边与角相同的角:
