1.2 角的概念的推广 课件2
图片预览







文档简介
课件20张PPT。第一章 三角函数1.2 角的概念的推广学习目标1、通过具体实例,认识角的概念推广的必要性.掌握用“旋转”定义角的概念
2、理解并掌握“正角”、“负角”、“零角”的含义
3、体会运动变化观点,深刻理解推广后的角的概念新课引入 初中是如何定义角的呢?其角的范围是什么?
定义1:从一个点出发引出的两条射线构成的几何图形叫做角。
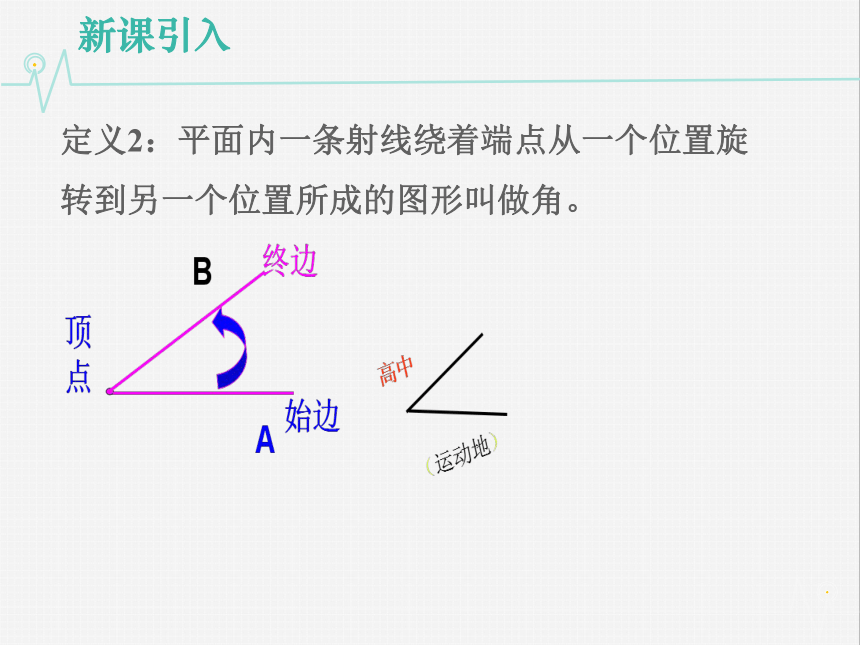
这种概念的优点是形象、直观、容易理解,但它是从图形形状来定义角,因此角的范围是[0o, 360o),这种定义称为静态定义,其弊端在于“狭隘”。新课引入定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。新课引入生活中有很多实例
如:体操运动员转体720o,跳水运动员向内、向外
转体1080o,各转了多少度?
这些例子不仅角范围不在 [0o, 360o) ,而且方向不同,有必要将角的概念推广到任意角。
想想用什么办法才能推广到任意角?
关键是用运动的观点来看待角的变化。 探究点1定义(“旋转”形成角): 一条射线由原来的位置OA,绕着它的端点O按一定的方向旋转到另一位置OB,就形成角α.
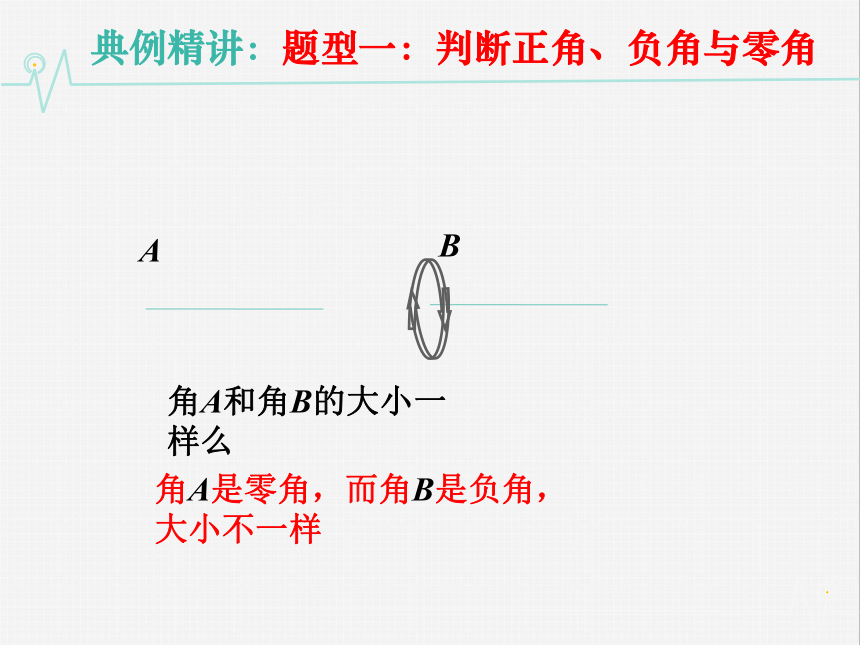
旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.角的概念的推广探究点2 在平面内,一条射线绕它的端点旋转有两个相反的方向:顺时针方向和逆时针方向。习惯上规定,按照逆时针方向旋转而成的角叫做正角;按照顺时针方向旋转成的角叫做负角;当射线没有旋转时,我们也把它看成一个角,叫做零角。基本概念探究点2 当射线绕其端点按照逆时针方向或按照顺时针方向旋转时,旋转的绝对量可以是任意的。在画图时,常用带箭头的弧来表示旋转的方向和旋转的绝对量。旋转生成的角,又常叫做转角。典例精讲:题型一:判断正角、负角与零角AB角A和角B的大小一样么角A是零角,而角B是负角,大小不一样典例精讲:题型一:判断正角、负角与零角判断下列角的符号BCB为负角,C为正角探究点4用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分;
② 角可以任意大;
实例:体操动作:旋转2周(360°×2=720°)3周(360°×3=1080°)
③ 还有零角, 一条射线,没有旋转.角的概念扩展的意义:探究点4 角的概念推广以后,它包括任意大小的正角、负角和零角。要注意,正角和负角是表示具有相反意义的旋转量,它的正负规定纯属于习惯,就好象与正数、负数的规定一样,零角无正负,就好象数零无正负一样.典例精讲:题型二:比较角的大小ABC比较三个角的大小角C>角B>角A典例精讲:题型二:比较角的大小 判断角的正负主要根据角的旋转方向,即由始边到终边的方向,角B由始边到终边是顺时针旋转为负,角C由始边到终边是逆时针旋转为正。
故角B是负角,角C是正角探究点51:角的正负由旋转方向决定
2:角可以任意大小,绝对值大小由旋转次数及终边位置决定
3.用旋转来描述角,需要注意三个要素
(旋转中心、旋转方向和旋转量) 拓展提升:题型二:根据角A写出角B与角C的大小ABC角B为-30°,角C为-150°课堂练习给下列角按由大到小排序角C>角A>角BABC课堂练习根据角A写出角B与角C的度数A 145°BC课堂练习 解:角A为145 °,因为角B是顺时针旋转,所以角B为-145 °,角C逆时针旋转,且是角A的补角,因此叫C为215 °归纳小结从图形形状来定义角,因此角的范围是[0o, 360o),这种定义称为静态定义,其弊端在于“狭隘”.
2. 用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分;
② 角可以任意大;
2、理解并掌握“正角”、“负角”、“零角”的含义
3、体会运动变化观点,深刻理解推广后的角的概念新课引入 初中是如何定义角的呢?其角的范围是什么?
定义1:从一个点出发引出的两条射线构成的几何图形叫做角。
这种概念的优点是形象、直观、容易理解,但它是从图形形状来定义角,因此角的范围是[0o, 360o),这种定义称为静态定义,其弊端在于“狭隘”。新课引入定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。新课引入生活中有很多实例
如:体操运动员转体720o,跳水运动员向内、向外
转体1080o,各转了多少度?
这些例子不仅角范围不在 [0o, 360o) ,而且方向不同,有必要将角的概念推广到任意角。
想想用什么办法才能推广到任意角?
关键是用运动的观点来看待角的变化。 探究点1定义(“旋转”形成角): 一条射线由原来的位置OA,绕着它的端点O按一定的方向旋转到另一位置OB,就形成角α.
旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.角的概念的推广探究点2 在平面内,一条射线绕它的端点旋转有两个相反的方向:顺时针方向和逆时针方向。习惯上规定,按照逆时针方向旋转而成的角叫做正角;按照顺时针方向旋转成的角叫做负角;当射线没有旋转时,我们也把它看成一个角,叫做零角。基本概念探究点2 当射线绕其端点按照逆时针方向或按照顺时针方向旋转时,旋转的绝对量可以是任意的。在画图时,常用带箭头的弧来表示旋转的方向和旋转的绝对量。旋转生成的角,又常叫做转角。典例精讲:题型一:判断正角、负角与零角AB角A和角B的大小一样么角A是零角,而角B是负角,大小不一样典例精讲:题型一:判断正角、负角与零角判断下列角的符号BCB为负角,C为正角探究点4用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分;
② 角可以任意大;
实例:体操动作:旋转2周(360°×2=720°)3周(360°×3=1080°)
③ 还有零角, 一条射线,没有旋转.角的概念扩展的意义:探究点4 角的概念推广以后,它包括任意大小的正角、负角和零角。要注意,正角和负角是表示具有相反意义的旋转量,它的正负规定纯属于习惯,就好象与正数、负数的规定一样,零角无正负,就好象数零无正负一样.典例精讲:题型二:比较角的大小ABC比较三个角的大小角C>角B>角A典例精讲:题型二:比较角的大小 判断角的正负主要根据角的旋转方向,即由始边到终边的方向,角B由始边到终边是顺时针旋转为负,角C由始边到终边是逆时针旋转为正。
故角B是负角,角C是正角探究点51:角的正负由旋转方向决定
2:角可以任意大小,绝对值大小由旋转次数及终边位置决定
3.用旋转来描述角,需要注意三个要素
(旋转中心、旋转方向和旋转量) 拓展提升:题型二:根据角A写出角B与角C的大小ABC角B为-30°,角C为-150°课堂练习给下列角按由大到小排序角C>角A>角BABC课堂练习根据角A写出角B与角C的度数A 145°BC课堂练习 解:角A为145 °,因为角B是顺时针旋转,所以角B为-145 °,角C逆时针旋转,且是角A的补角,因此叫C为215 °归纳小结从图形形状来定义角,因此角的范围是[0o, 360o),这种定义称为静态定义,其弊端在于“狭隘”.
2. 用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分;
② 角可以任意大;
