1.4.1-1.4.2 任意角的正弦函数、余弦函数的定义 课件3
文档属性
| 名称 | 1.4.1-1.4.2 任意角的正弦函数、余弦函数的定义 课件3 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 09:59:25 | ||
图片预览










文档简介
课件37张PPT。三角函数第一章4 正弦函数和余弦函数的定义与诱导公式第一章1.4.1-1.4.2.任意角的正弦函数、余弦函数的定义1.任意角的正弦函数、余弦函数的定义
(1)单位圆
在直角坐标系中,以_______为圆心,以__________为半径的圆,称为单位圆.
(2)任意角的正弦、余弦函数的定义
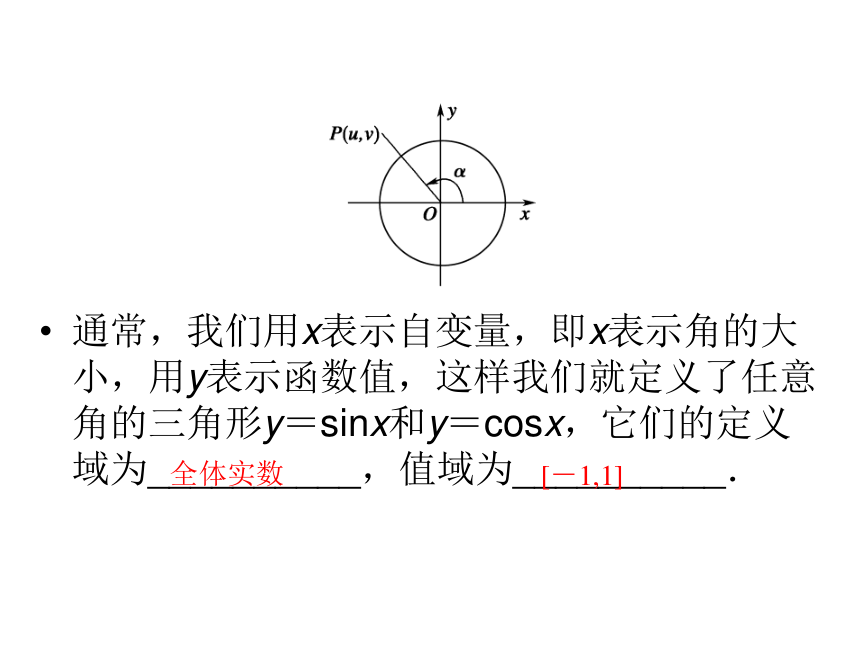
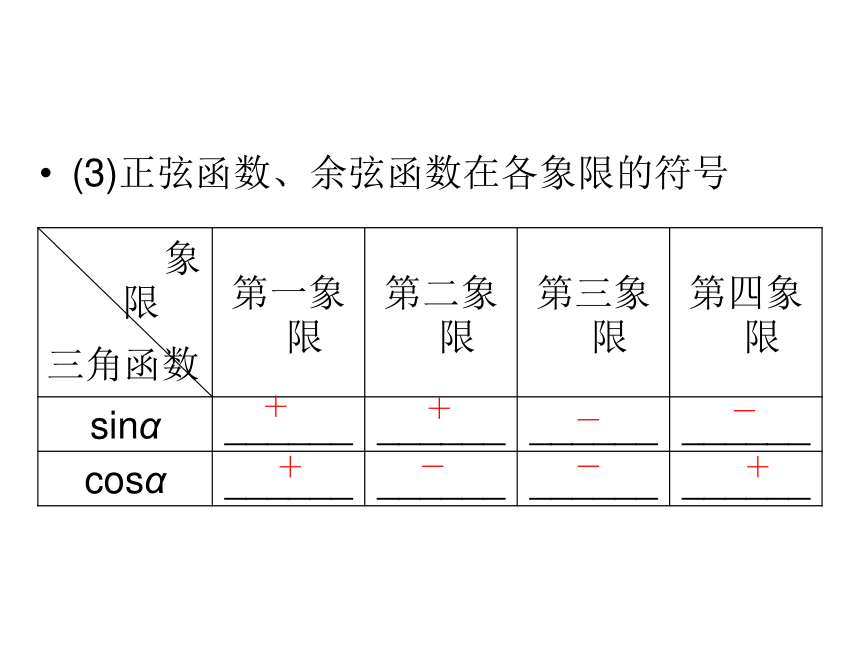
定义1:如图所示,在直角坐标系中,给定单位圆对于任意角α,使角α的顶点与原点重合,始边与x轴正半轴重合,终边与单位圆交于点P(u,v),那么点P的__________v叫作角α的正弦函数,记作__________;点P的__________u叫作角α的余弦函数,记作__________.原点 单位长 纵坐标 v=sinα 横坐标 u=cosα 通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角形y=sinx和y=cosx,它们的定义域为__________,值域为__________.全体实数 [-1,1] (3)正弦函数、余弦函数在各象限的符号+ + - - + - - + 2.单位圆与周期性
(1)终边相同的角的正、余弦函数值__________
sin(2kπ+x)=__________,k∈Z.
cos(2kπ+x)=__________,k∈Z.
(2)周期函数与周期
一般地,对于函数f(x),如果存在非零实数T,对定义域内的任意一个x值,都有______________,我们就把f(x)称为周期函数,T称为这个函数的__________.相等 sinx cosx f(x+T)=f(x) 周期 [答案] B[答案] D
3.已知θ是第四象限角,则( )
A.sinθ>0,cosθ>0 B.sinθ>0,cosθ<0
C.sinθ<0,cosθ>0 D.sinθ<0,cosθ<0
[答案] C
[解析] 因为θ为第四象限角,根据各象限角的三角函数定义可知sinθ<0,cosθ>0.
4.5sin90°+2sin0°-3sin270°+10cos180°=__________.
[答案] -2
[解析] ∵sin90°=1,sin0°=0,
sin270°=-1,cos180°=-1,
∴原式=5×1+2×0-3×(-1)+10×(-1)=-2.
5.已知函数f(x)是周期函数,周期T=6,f(2)=1,则f(14)=__________.
[答案] 1
[解析] f(14)=f(2×6+2)=f(2)=1.[思路分析] 角θ的终边可能在第三象限或第四象限,分两种情况讨论.三角函数的定义
[规律总结] (1)当角α的终边上点的坐标以参数形式给出或含有绝对值时,要根据问题及解题的需要对参数进行分类讨论.
(2)求任意角的三角函数,有时需要确定角所在的象限,相应地以此来确定三角函数的符号,这是容易出现错误的地方.已知角α的终边经过点P(-4a,3a)(a≠0).
(1)求sinα,cosα的值;
(2)求α的终边与单位圆交点Q的坐标.[思路分析] 确定4rad,8rad所在象限,则符号易定.正弦、余弦函数值符号的确定
[规律总结] 对于此类判断含三角函数的代数式的符号问题,关键是要搞清楚三角函数中所含的角是第几象限角,再根据正、余弦函数值在各象限的符号确定函数值的正负,进而得到结果.其中,正弦、余弦函数周期的运用对判断角所在的象限也很重要.
(2)∵-925°=-3×360°+155°,
∴-925°是第二象限角.
∴cos(-925°)<0.
(3)∵340°是第四象限角,265°是第三象限角,
∴sin340°<0,cos265°<0,∴sin340°·cos265°>0.[思路分析] 先利用终边相同的角的公式转化,然后求值.利用终边相同的角的公式化简、求值 [规律总结] 解答此类题目的方式是先把已知角借助于终边相同的角化归到[0,2π)之间,然后利用公式化简求值;在问题的解答过程中重在体现数学上的化归(转化)思想.[思路分析] 只需找出一个常数T(T≠0),满足f(x+T)=f(x)即可.
[证明] ∵f(x+2a)=f[(x+a)+a]=-f(x+a)=-[-f(x)]=f(x),
∴f(x)是周期函数,且2a是它的一个周期.周期函数的理解与应用
[规律总结] (1)周期的定义是对定义域中每一个x值来说的.如果只有个别的x值满足f(x+T)=f(x),则不能说T是f(x)的周期.
(2)从等式f(x+T)=f(x)来看,应强调自变量x本身加的常数才是周期.如f(2x+T)=f(x)的周期,不能说T是f(x)的周期.已知函数f(x)是以2为周期的奇函数,f(1)=3,
求f(-7)的值.
[解析] 由题意知f(-7)=-f(7),
∵f(7)=f(3×2+1)=f(1)=3,∴f(-7)=-3.[辨析] 错解一是对sinα=y,cosα=x的理解有误,定义中的(x,y)是α终边与单位圆的交点坐标,不是任意点.
错解二只考虑了y=-3x(x>0)的情况,没考虑y=-3x(x<0)的情况.
(1)单位圆
在直角坐标系中,以_______为圆心,以__________为半径的圆,称为单位圆.
(2)任意角的正弦、余弦函数的定义
定义1:如图所示,在直角坐标系中,给定单位圆对于任意角α,使角α的顶点与原点重合,始边与x轴正半轴重合,终边与单位圆交于点P(u,v),那么点P的__________v叫作角α的正弦函数,记作__________;点P的__________u叫作角α的余弦函数,记作__________.原点 单位长 纵坐标 v=sinα 横坐标 u=cosα 通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角形y=sinx和y=cosx,它们的定义域为__________,值域为__________.全体实数 [-1,1] (3)正弦函数、余弦函数在各象限的符号+ + - - + - - + 2.单位圆与周期性
(1)终边相同的角的正、余弦函数值__________
sin(2kπ+x)=__________,k∈Z.
cos(2kπ+x)=__________,k∈Z.
(2)周期函数与周期
一般地,对于函数f(x),如果存在非零实数T,对定义域内的任意一个x值,都有______________,我们就把f(x)称为周期函数,T称为这个函数的__________.相等 sinx cosx f(x+T)=f(x) 周期 [答案] B[答案] D
3.已知θ是第四象限角,则( )
A.sinθ>0,cosθ>0 B.sinθ>0,cosθ<0
C.sinθ<0,cosθ>0 D.sinθ<0,cosθ<0
[答案] C
[解析] 因为θ为第四象限角,根据各象限角的三角函数定义可知sinθ<0,cosθ>0.
4.5sin90°+2sin0°-3sin270°+10cos180°=__________.
[答案] -2
[解析] ∵sin90°=1,sin0°=0,
sin270°=-1,cos180°=-1,
∴原式=5×1+2×0-3×(-1)+10×(-1)=-2.
5.已知函数f(x)是周期函数,周期T=6,f(2)=1,则f(14)=__________.
[答案] 1
[解析] f(14)=f(2×6+2)=f(2)=1.[思路分析] 角θ的终边可能在第三象限或第四象限,分两种情况讨论.三角函数的定义
[规律总结] (1)当角α的终边上点的坐标以参数形式给出或含有绝对值时,要根据问题及解题的需要对参数进行分类讨论.
(2)求任意角的三角函数,有时需要确定角所在的象限,相应地以此来确定三角函数的符号,这是容易出现错误的地方.已知角α的终边经过点P(-4a,3a)(a≠0).
(1)求sinα,cosα的值;
(2)求α的终边与单位圆交点Q的坐标.[思路分析] 确定4rad,8rad所在象限,则符号易定.正弦、余弦函数值符号的确定
[规律总结] 对于此类判断含三角函数的代数式的符号问题,关键是要搞清楚三角函数中所含的角是第几象限角,再根据正、余弦函数值在各象限的符号确定函数值的正负,进而得到结果.其中,正弦、余弦函数周期的运用对判断角所在的象限也很重要.
(2)∵-925°=-3×360°+155°,
∴-925°是第二象限角.
∴cos(-925°)<0.
(3)∵340°是第四象限角,265°是第三象限角,
∴sin340°<0,cos265°<0,∴sin340°·cos265°>0.[思路分析] 先利用终边相同的角的公式转化,然后求值.利用终边相同的角的公式化简、求值 [规律总结] 解答此类题目的方式是先把已知角借助于终边相同的角化归到[0,2π)之间,然后利用公式化简求值;在问题的解答过程中重在体现数学上的化归(转化)思想.[思路分析] 只需找出一个常数T(T≠0),满足f(x+T)=f(x)即可.
[证明] ∵f(x+2a)=f[(x+a)+a]=-f(x+a)=-[-f(x)]=f(x),
∴f(x)是周期函数,且2a是它的一个周期.周期函数的理解与应用
[规律总结] (1)周期的定义是对定义域中每一个x值来说的.如果只有个别的x值满足f(x+T)=f(x),则不能说T是f(x)的周期.
(2)从等式f(x+T)=f(x)来看,应强调自变量x本身加的常数才是周期.如f(2x+T)=f(x)的周期,不能说T是f(x)的周期.已知函数f(x)是以2为周期的奇函数,f(1)=3,
求f(-7)的值.
[解析] 由题意知f(-7)=-f(7),
∵f(7)=f(3×2+1)=f(1)=3,∴f(-7)=-3.[辨析] 错解一是对sinα=y,cosα=x的理解有误,定义中的(x,y)是α终边与单位圆的交点坐标,不是任意点.
错解二只考虑了y=-3x(x>0)的情况,没考虑y=-3x(x<0)的情况.
