1.4.3 单位圆与诱导公式 课件1
文档属性
| 名称 | 1.4.3 单位圆与诱导公式 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 379.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 10:00:30 | ||
图片预览








文档简介
课件26张PPT。1.4.3 单位圆与诱导公式第一章 三角函数课前自主学习学习要求掌握同角三角函数的基本关系式;
2. 熟练运用基本关系式公式求值;
3. 培养学生分析问题解决问题的能力。
自学导引上节课我们已学习了任意角三角函数定义,如图所示,任意角α三角函数是如何定义的呢?P(x,y)Oxy1MA(1,0)αsinα=_______
cosα=_______
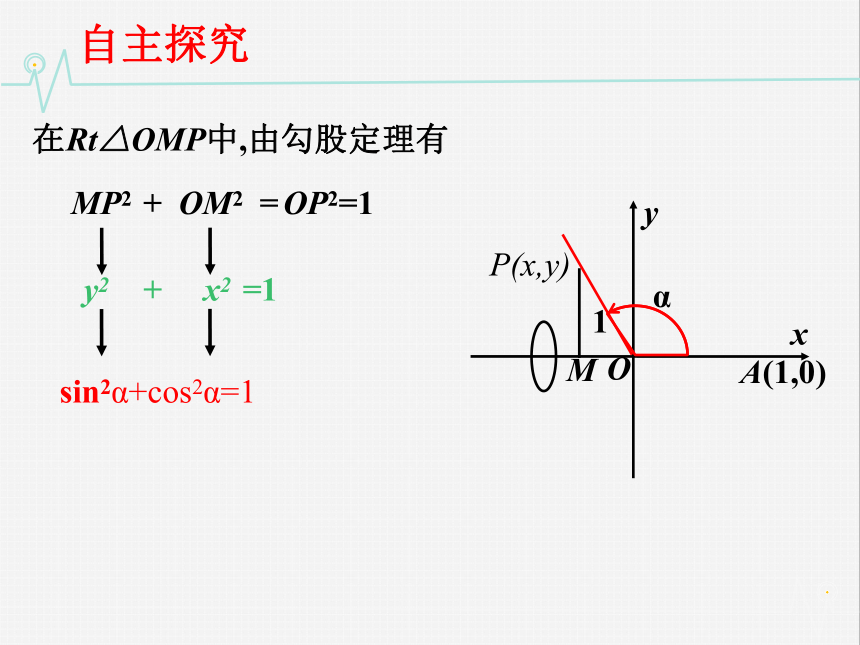
tanα=_______yx自主探究Oxy1MA(1,0)α在Rt△OMP中,由勾股定理有 MP2 + OM2 =P(x,y)OP2=1预习测评 已知:sina = 0.8,填空:cosa = ______哈哈~~~~~~~~
我换了个马甲!小样!别以为你换了个马甲我就认不出你了!0.6±预习测评因α是第三角限角,所以课堂讲练互动要点阐释sin2α+cos2α=1要点阐释 对于上述两种关系可作哪些变形?典例剖析题型一 解:因为sinα<0,sinα≠1,所以α是第三或第四象限角如果α是第三象限角,那么cosα<0.于是如果α是第四象限角,那么 已知:sina = - 0.8,且a 为第三象限角,求:cosa,tana ,cota 的值.解:∵ a 为第三象限角,∴ cosa < 0 ,于是从而题型二 三角函数式的化简
化简三角函数式的一般要求是:
(1)尽量使函数种类最少,项数最少,次数最低;
(2)尽量使分母不含三角函数式;
(3)根号内的三角函数式尽量开出来;
(4)能求得数值的应计算出来.
注意在对三角函数式变形时,常将式子中的“1”作巧妙的变形.
题型三 【证明】
(1)左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α=sin2α-(1-sin2α)
=2sin2α-1=右边,
∴sin4α-cos4α=2sin2α-1.题型三 题型三 证明三角恒等式常用的方法有:
(1)由繁到简,从结构复杂的一边入手,经过适当的变形、配凑,向结构简单的一边化简,或从等式两边同时入手,使它们等于同一个数(式).
(2)从已知或已证的恒等式出发,根据定理、公式进行恒等变形,推导出求证的恒等式.
(3)比较法,证明待证等式的左、右两边之差为0.
(4)从待证的恒等式出发,利用三角恒等变形公式,找出一个显然成立的恒等式或已有的结论.详细解析:纠错心得:课堂总结(1)同角三角函数的关系式的前提是“同角”,(2) 条件等式,即它们成立的前提是表达式有意义.(3)利用平方关系时,往往要开方,因此要先根据角所在象限确定符号,即要就角所在象限进行分类讨论.
2. 熟练运用基本关系式公式求值;
3. 培养学生分析问题解决问题的能力。
自学导引上节课我们已学习了任意角三角函数定义,如图所示,任意角α三角函数是如何定义的呢?P(x,y)Oxy1MA(1,0)αsinα=_______
cosα=_______
tanα=_______yx自主探究Oxy1MA(1,0)α在Rt△OMP中,由勾股定理有 MP2 + OM2 =P(x,y)OP2=1预习测评 已知:sina = 0.8,填空:cosa = ______哈哈~~~~~~~~
我换了个马甲!小样!别以为你换了个马甲我就认不出你了!0.6±预习测评因α是第三角限角,所以课堂讲练互动要点阐释sin2α+cos2α=1要点阐释 对于上述两种关系可作哪些变形?典例剖析题型一 解:因为sinα<0,sinα≠1,所以α是第三或第四象限角如果α是第三象限角,那么cosα<0.于是如果α是第四象限角,那么 已知:sina = - 0.8,且a 为第三象限角,求:cosa,tana ,cota 的值.解:∵ a 为第三象限角,∴ cosa < 0 ,于是从而题型二 三角函数式的化简
化简三角函数式的一般要求是:
(1)尽量使函数种类最少,项数最少,次数最低;
(2)尽量使分母不含三角函数式;
(3)根号内的三角函数式尽量开出来;
(4)能求得数值的应计算出来.
注意在对三角函数式变形时,常将式子中的“1”作巧妙的变形.
题型三 【证明】
(1)左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α=sin2α-(1-sin2α)
=2sin2α-1=右边,
∴sin4α-cos4α=2sin2α-1.题型三 题型三 证明三角恒等式常用的方法有:
(1)由繁到简,从结构复杂的一边入手,经过适当的变形、配凑,向结构简单的一边化简,或从等式两边同时入手,使它们等于同一个数(式).
(2)从已知或已证的恒等式出发,根据定理、公式进行恒等变形,推导出求证的恒等式.
(3)比较法,证明待证等式的左、右两边之差为0.
(4)从待证的恒等式出发,利用三角恒等变形公式,找出一个显然成立的恒等式或已有的结论.详细解析:纠错心得:课堂总结(1)同角三角函数的关系式的前提是“同角”,(2) 条件等式,即它们成立的前提是表达式有意义.(3)利用平方关系时,往往要开方,因此要先根据角所在象限确定符号,即要就角所在象限进行分类讨论.
