1.5.2 正弦函数的图像 课件
图片预览








文档简介
课件25张PPT。1.5.2 正弦函数的图像第一章 三角函数2课前自主学习学习要求1.了解正弦函数、余弦函数的图象.
2.会用“五点法”画出正弦函数、余弦函数的图象.自学导引遇到一个新函数,它总具有许多基本性质,要直观、全面了解基本特性,我们应从哪个方面入手?
自然是从它的图象入手,画出它的图象,观察图象的形状,看看它有什么特殊点,并借助它的图象研究它的性质,如:值域、单调性、奇偶性、最值等.
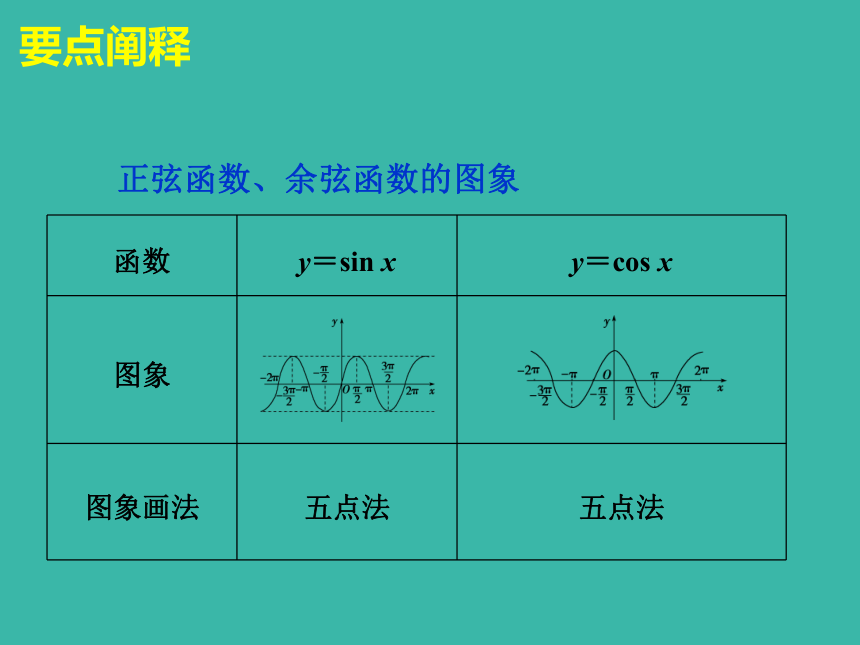
我们今天就学习自学导引作函数图象最原始的方法是什么?描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?答:列表、描点、连线自主探究预习测评课堂讲练互动要点阐释正弦函数、余弦函数的图象要点阐释(0,0)(π,0)(2π,0)要点阐释(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标);(2)描点(定出五个关键点);(3)连线(用光滑的曲线顺次连结点).典例剖析题型一 “五点法”作正弦函数、余弦函数的图象
画出下列函数的简图:
(1)y=1+cos x,x∈[0,2π]
(2)y=-sin x,x∈[0,2π].【解】 (1)画法:
①列表:
②描点:③连线:用平滑曲线依次连接各点,即得所求图象.
(2)画法:①列表:
②描点:1.用“五点法”作出函数y=sin x-1,x∈[0,2π]的简图.描点连线,如图:题型二 用三角函数的图象解sin x>a(或cos x>a)的方法:
①作出直线y=a,作出y=sin x(或y=cos x)的图象;
②确定sin x=a(或cos x=a)的x值;
③确定sin x>a(或cos x>a)的解集.
解析:如图所示.答案:2误区解密:【常见错误】 (1)在化简过程中,易忽视该函数的定义域,造成化简前后不等价,从而所画图象不正确.
(2)正、余弦函数五点坐标互混而出错.纠错心得:【失误防范】
(1)首先观察所给表达式是否需要化简,化简后是否与原函数等价.
(2)牢记正、余弦函数五个关键点的坐标.
(3)注意图象的平滑.
课堂总结1、正弦函数、余弦函数图象的几种不同的画法以及其优缺点
2、五点法作简图
2.会用“五点法”画出正弦函数、余弦函数的图象.自学导引遇到一个新函数,它总具有许多基本性质,要直观、全面了解基本特性,我们应从哪个方面入手?
自然是从它的图象入手,画出它的图象,观察图象的形状,看看它有什么特殊点,并借助它的图象研究它的性质,如:值域、单调性、奇偶性、最值等.
我们今天就学习自学导引作函数图象最原始的方法是什么?描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?答:列表、描点、连线自主探究预习测评课堂讲练互动要点阐释正弦函数、余弦函数的图象要点阐释(0,0)(π,0)(2π,0)要点阐释(五点作图法)(1)列表(列出对图象形状起关键作用的五点坐标);(2)描点(定出五个关键点);(3)连线(用光滑的曲线顺次连结点).典例剖析题型一 “五点法”作正弦函数、余弦函数的图象
画出下列函数的简图:
(1)y=1+cos x,x∈[0,2π]
(2)y=-sin x,x∈[0,2π].【解】 (1)画法:
①列表:
②描点:③连线:用平滑曲线依次连接各点,即得所求图象.
(2)画法:①列表:
②描点:1.用“五点法”作出函数y=sin x-1,x∈[0,2π]的简图.描点连线,如图:题型二 用三角函数的图象解sin x>a(或cos x>a)的方法:
①作出直线y=a,作出y=sin x(或y=cos x)的图象;
②确定sin x=a(或cos x=a)的x值;
③确定sin x>a(或cos x>a)的解集.
解析:如图所示.答案:2误区解密:【常见错误】 (1)在化简过程中,易忽视该函数的定义域,造成化简前后不等价,从而所画图象不正确.
(2)正、余弦函数五点坐标互混而出错.纠错心得:【失误防范】
(1)首先观察所给表达式是否需要化简,化简后是否与原函数等价.
(2)牢记正、余弦函数五个关键点的坐标.
(3)注意图象的平滑.
课堂总结1、正弦函数、余弦函数图象的几种不同的画法以及其优缺点
2、五点法作简图
