1.6 余弦函数的图像与性质 课件2
文档属性
| 名称 | 1.6 余弦函数的图像与性质 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览











文档简介
课件30张PPT。1.6.1-1.6.2 余弦函数的图像与性质第一章 三角函数课前自主学习1.掌握y=sin x,y=cos x的最大值与最小值.
2.会求简单三角函数的值域和最值.学习要求1.正弦函数、余弦函数的定义域都是_____,值域都是____________.
2.正弦函数、余弦函数的最大值都是____,最小值都是________.
R[-1,1]1自学导引-1自学导引3.对于正弦函数y=sin x,x∈R有:
当且仅当x= 时,取得最大值1;
当且仅当x= 时,取得最小值-1.
自学导引4.对于余弦函数y=cos x,x∈R有:
当且仅当x= 时,取得最大值1;
当且仅当x= 时,取得最小值-1.
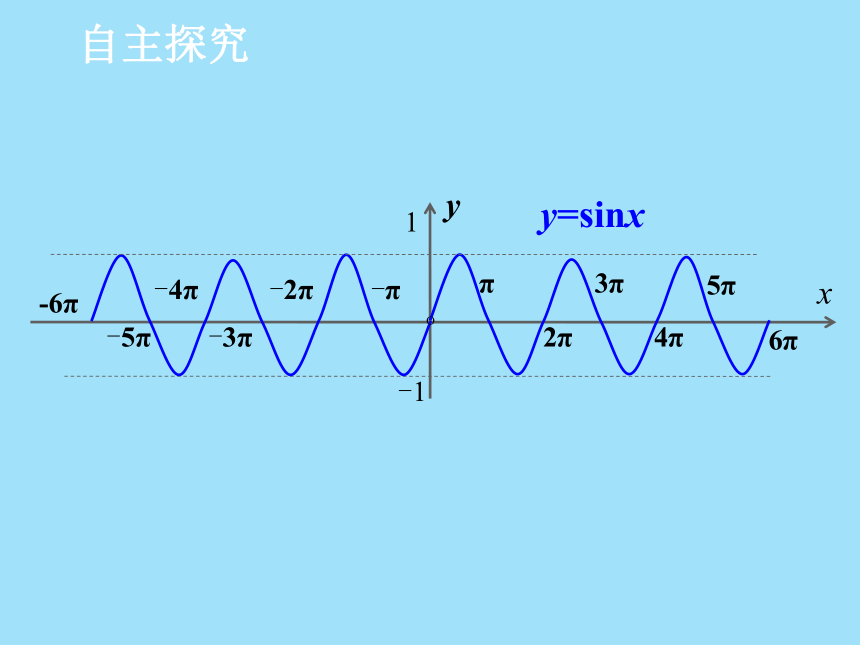
自主探究1.观察正弦曲线和余弦曲线,正、余弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?存在,最大值为1,最小值为-1.自主探究自主探究自主探究2.当自变量x分别取何值时,正弦函数y=sinx取得最大值1和最小值-1?正弦函数当且仅当 时取最大值1,
当且仅当 时取最小值-1 .自主探究3.当自变量x分别取何值时,余弦函数y=cosx取得最大值1和最小值-1?余弦函数当且仅当 时取最大值1,
当且仅当 时取最小值-1. 4.函数y=Asinωx(A >0,ω≠0)的值域是什么?它的值域[-A, A]. 自主探究11.函数y=2sinx+1的值域是________.预习测评解析:∵-1≤sin x≤1,∴-1≤2sin x+1≤3[-1,3]2.M和m分别表示函数y=2cos x-1的最大值和最小值,则M+m等于( )
A.-2 B.2 C. 3 D.-3
预习测评A解析:函数的最大值为M =2-1=1,函数的最小值为m=-2-1=-3, M+m=-2,故选A.3.当x=____________________ _时,函数
取得最小值-1.
预习测评解析:由 ,k∈Z
得: (k∈Z).课堂讲练互动 正弦函数y=sinx,x ?R,1.正弦函数的最值要点阐释2.余弦函数的最值 余弦函数y=cosx,x ?R,要点阐释函数y=Asin(wx+φ)+b,(A>0)x∈R
最大值为A+b ,最小值为-A+b.
要点阐释3.函数y=Asin(wx+φ)+b,x∈R的最大值、最小值. 例1、 求使下列函数取得最大值的自变量x的集合,
并说出最大值是什么.典型例题(1) y=sin2x,x∈R; (2) y=sin(3x+ ) -1 解:(1) 令w=2x,那么x∈R得Z∈R,且使函数y=sinw,w∈R,取得最大值的集合是{w|w= +2kπ,k∈Z}由2x=w= +2kπ,题型一 求正弦函数、余弦函数的最值函数y=sin2x,x∈R的最大值是1.典型例题(2) 当3x+ =2k?+ 即 x= (k?Z)时, y的最大值为0.点评:求自变量x的取值的集合,关键是运用整体带入的思想,将wx+φ看成一个整体带入,利用正弦函数、余弦函数取最大值、最小值时自变量的取值计算即可 .1.函数y=1-λcosx的最大值与最小值的差等于2,则实数λ的值为_______.
1或-1解析: ∵x∈R,∴
当λ>0时,ymax=1+ λ,ymin=1-λ
由题意,得(1+λ)-(1-λ)=2,∴λ=1,
当λ<0时,同理可得λ=-1.
综上: λ=1或-1.例2.求函数 的最大值和最小值,并写出取得最值时的x取值集合.题型二 求y=Asin(ωx+φ)+b的最值解析:∵-1≤ ≤1,
∴当 =1时,ymax=5,
此时2x+ = +2kπ(k∈Z),
即x= +kπ(k∈Z),题型二 求y=Asin(ωx+φ)+b的最值点评:求有关y=Asin(ωx+φ)+b,x∈R的最值或值域这类题目的关键在于充分利用好正弦函数y=sin x的有界性,即|sin x|≤1. 2.求使函数y=2sin 3 x+1,x∈R取得最大值的自变量x的集合,并说出最大值是什么? 解析:当sin 3x=1,即
得 (k∈Z)时.函数y取得最大值为3,此时,自变量x的集合为
误区解密:因忽略有向线段的方向而出错正解: ∵函数y=sin x,x∈ ,在区间 上单调递增,在 上单调递减.
∴ymax=sin =1,ymin=sin = ,
∴该函数的值域为 .错解:[ - 1,1].错因分析:错解没有注意到x的取值范围,当x∈
时, y=sin x最小值 取不到-1 .例3.函数y=sin x,x∈ 的值域是________.
正弦函数、余弦函数的最大值都是1,最小值都是-1,前提条件是定义域为R,当限制函数的定义域时,一定要根据函数的单调性求指定区间上函数的最大值、最小值.纠错心得:课堂总结1.正弦函数y=sinx,x∈R的最大值、最小值.
2.余弦函数y=cosx,x∈R的最大值、最小值.
3.函数y=Asin(wx+φ)+b,x∈R的最大值、最小值.
2.会求简单三角函数的值域和最值.学习要求1.正弦函数、余弦函数的定义域都是_____,值域都是____________.
2.正弦函数、余弦函数的最大值都是____,最小值都是________.
R[-1,1]1自学导引-1自学导引3.对于正弦函数y=sin x,x∈R有:
当且仅当x= 时,取得最大值1;
当且仅当x= 时,取得最小值-1.
自学导引4.对于余弦函数y=cos x,x∈R有:
当且仅当x= 时,取得最大值1;
当且仅当x= 时,取得最小值-1.
自主探究1.观察正弦曲线和余弦曲线,正、余弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?存在,最大值为1,最小值为-1.自主探究自主探究自主探究2.当自变量x分别取何值时,正弦函数y=sinx取得最大值1和最小值-1?正弦函数当且仅当 时取最大值1,
当且仅当 时取最小值-1 .自主探究3.当自变量x分别取何值时,余弦函数y=cosx取得最大值1和最小值-1?余弦函数当且仅当 时取最大值1,
当且仅当 时取最小值-1. 4.函数y=Asinωx(A >0,ω≠0)的值域是什么?它的值域[-A, A]. 自主探究11.函数y=2sinx+1的值域是________.预习测评解析:∵-1≤sin x≤1,∴-1≤2sin x+1≤3[-1,3]2.M和m分别表示函数y=2cos x-1的最大值和最小值,则M+m等于( )
A.-2 B.2 C. 3 D.-3
预习测评A解析:函数的最大值为M =2-1=1,函数的最小值为m=-2-1=-3, M+m=-2,故选A.3.当x=____________________ _时,函数
取得最小值-1.
预习测评解析:由 ,k∈Z
得: (k∈Z).课堂讲练互动 正弦函数y=sinx,x ?R,1.正弦函数的最值要点阐释2.余弦函数的最值 余弦函数y=cosx,x ?R,要点阐释函数y=Asin(wx+φ)+b,(A>0)x∈R
最大值为A+b ,最小值为-A+b.
要点阐释3.函数y=Asin(wx+φ)+b,x∈R的最大值、最小值. 例1、 求使下列函数取得最大值的自变量x的集合,
并说出最大值是什么.典型例题(1) y=sin2x,x∈R; (2) y=sin(3x+ ) -1 解:(1) 令w=2x,那么x∈R得Z∈R,且使函数y=sinw,w∈R,取得最大值的集合是{w|w= +2kπ,k∈Z}由2x=w= +2kπ,题型一 求正弦函数、余弦函数的最值函数y=sin2x,x∈R的最大值是1.典型例题(2) 当3x+ =2k?+ 即 x= (k?Z)时, y的最大值为0.点评:求自变量x的取值的集合,关键是运用整体带入的思想,将wx+φ看成一个整体带入,利用正弦函数、余弦函数取最大值、最小值时自变量的取值计算即可 .1.函数y=1-λcosx的最大值与最小值的差等于2,则实数λ的值为_______.
1或-1解析: ∵x∈R,∴
当λ>0时,ymax=1+ λ,ymin=1-λ
由题意,得(1+λ)-(1-λ)=2,∴λ=1,
当λ<0时,同理可得λ=-1.
综上: λ=1或-1.例2.求函数 的最大值和最小值,并写出取得最值时的x取值集合.题型二 求y=Asin(ωx+φ)+b的最值解析:∵-1≤ ≤1,
∴当 =1时,ymax=5,
此时2x+ = +2kπ(k∈Z),
即x= +kπ(k∈Z),题型二 求y=Asin(ωx+φ)+b的最值点评:求有关y=Asin(ωx+φ)+b,x∈R的最值或值域这类题目的关键在于充分利用好正弦函数y=sin x的有界性,即|sin x|≤1. 2.求使函数y=2sin 3 x+1,x∈R取得最大值的自变量x的集合,并说出最大值是什么? 解析:当sin 3x=1,即
得 (k∈Z)时.函数y取得最大值为3,此时,自变量x的集合为
误区解密:因忽略有向线段的方向而出错正解: ∵函数y=sin x,x∈ ,在区间 上单调递增,在 上单调递减.
∴ymax=sin =1,ymin=sin = ,
∴该函数的值域为 .错解:[ - 1,1].错因分析:错解没有注意到x的取值范围,当x∈
时, y=sin x最小值 取不到-1 .例3.函数y=sin x,x∈ 的值域是________.
正弦函数、余弦函数的最大值都是1,最小值都是-1,前提条件是定义域为R,当限制函数的定义域时,一定要根据函数的单调性求指定区间上函数的最大值、最小值.纠错心得:课堂总结1.正弦函数y=sinx,x∈R的最大值、最小值.
2.余弦函数y=cosx,x∈R的最大值、最小值.
3.函数y=Asin(wx+φ)+b,x∈R的最大值、最小值.
