1.6 余弦函数的图像与性质 课件4
文档属性
| 名称 | 1.6 余弦函数的图像与性质 课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 690.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览






文档简介
课件23张PPT。 1.6.1-1.6.2 余弦函数的图像与性质
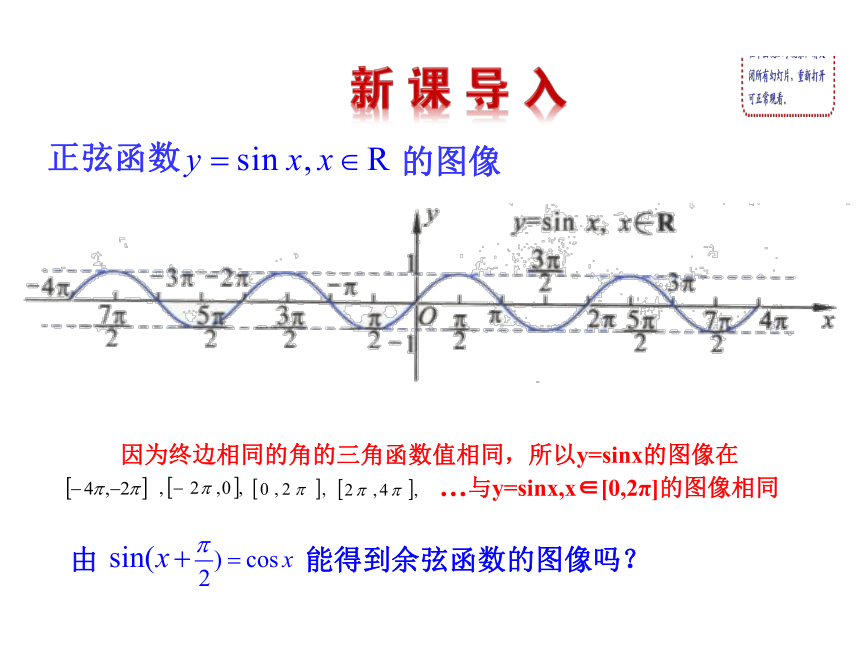
y因为终边相同的角的三角函数值相同,所以y=sinx的图像在
…与y=sinx,x∈[0,2π]的图像相同由 能得到余弦函数的图像吗?1.会用“图像变换法”和“五点法”作余弦函数的图像.(重点)
2.掌握余弦函数y=cosx的图像和性质.(重点)
3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.(难点)探究点1 余弦函数y=cosx (x∈R) 的图像 思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图像可以通过将正弦曲线向左平移 个单位长度而得到.余弦函数的图像叫作余弦曲线.根据诱导公式,可得:x6?yo-?-12?3?4?5?-2?-3?-4?1?余弦函数的图像 正弦函数的图像 y=cosx=sin(x+ ), x?R余弦曲线正弦曲线形状完全一样,只是位置不同方法:利用图像平移最高点:最低点:与x轴的交点:在函数 的图像上,起关键作用的点有:探究点2 余弦函数的性质-1余弦曲线:y=cosx,x∈R
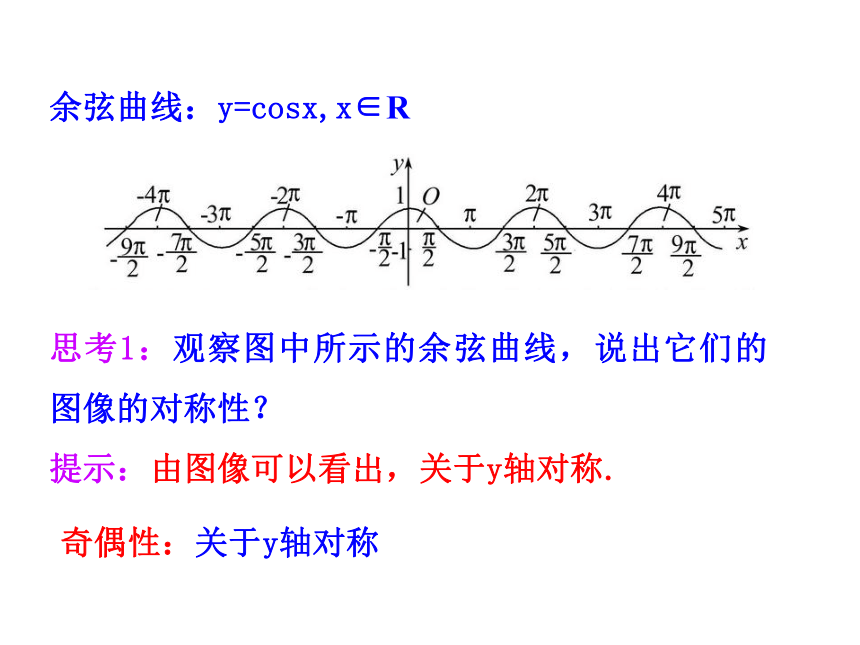
思考1:观察图中所示的余弦曲线,说出它们的图像的对称性?
提示:由图像可以看出,关于y轴对称.奇偶性:关于y轴对称思考2:如何判断三角函数的奇偶性?
提示:(1)利用图像法:若图像关于原点对称,则函数为奇函数;若图像关于y轴对称,则函数为偶函数.
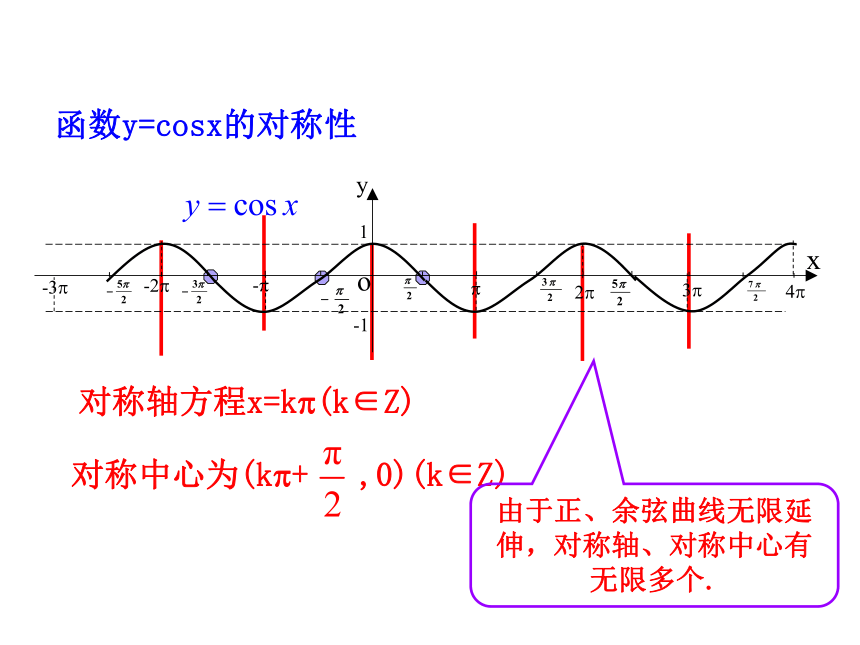
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.对称轴方程x=k?(k∈Z)对称中心为(k?+ ,0)(k∈Z)函数y=cosx的对称性由于正、余弦曲线无限延伸,对称轴、对称中心有无限多个.yxo-?-12?3?4?-2?-3?1?函数性质RRy=sinxy=cosx奇函数:图像关于原点对称偶函数:图像关于y轴对称单调性值 域提升总结:正弦和余弦函数的性质对比例1 画出函数 的简图,根据
图像讨论函数的性质.xy=cosx0 0-1-2-1 0 0-101解:列表1y=cosx-1y=cosx-1 yxo-?-12?3?4?-2?-3?1?-2y=cosxR[-2,0]偶函数2π思考交流:≥解:1.函数f(x)=cos4x,x∈R是( )
A.最小正周期为π的偶函数
B.最小正周期为π的奇函数
C.最小正周期为 的偶函数
D.最小正周期为 的奇函数C2.下列函数,在[ ,π]上增加的是( )
A.y=cos2x B.y=cosx
C.y=sin2x D.y=sinxA3.不求值比较下列两个三角函数值的大小.解:>4.对于实数范围内的x,分别写出满足sinx=cosx,sinx>cosx,sinx2.用“五点法”和“图像变换法”作余弦函数的图像. 被人揭下面具是一种失败,自己揭下面具却是一种胜利.
——雨果
y因为终边相同的角的三角函数值相同,所以y=sinx的图像在
…与y=sinx,x∈[0,2π]的图像相同由 能得到余弦函数的图像吗?1.会用“图像变换法”和“五点法”作余弦函数的图像.(重点)
2.掌握余弦函数y=cosx的图像和性质.(重点)
3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.(难点)探究点1 余弦函数y=cosx (x∈R) 的图像 思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图像可以通过将正弦曲线向左平移 个单位长度而得到.余弦函数的图像叫作余弦曲线.根据诱导公式,可得:x6?yo-?-12?3?4?5?-2?-3?-4?1?余弦函数的图像 正弦函数的图像 y=cosx=sin(x+ ), x?R余弦曲线正弦曲线形状完全一样,只是位置不同方法:利用图像平移最高点:最低点:与x轴的交点:在函数 的图像上,起关键作用的点有:探究点2 余弦函数的性质-1余弦曲线:y=cosx,x∈R
思考1:观察图中所示的余弦曲线,说出它们的图像的对称性?
提示:由图像可以看出,关于y轴对称.奇偶性:关于y轴对称思考2:如何判断三角函数的奇偶性?
提示:(1)利用图像法:若图像关于原点对称,则函数为奇函数;若图像关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.对称轴方程x=k?(k∈Z)对称中心为(k?+ ,0)(k∈Z)函数y=cosx的对称性由于正、余弦曲线无限延伸,对称轴、对称中心有无限多个.yxo-?-12?3?4?-2?-3?1?函数性质RRy=sinxy=cosx奇函数:图像关于原点对称偶函数:图像关于y轴对称单调性值 域提升总结:正弦和余弦函数的性质对比例1 画出函数 的简图,根据
图像讨论函数的性质.xy=cosx0 0-1-2-1 0 0-101解:列表1y=cosx-1y=cosx-1 yxo-?-12?3?4?-2?-3?1?-2y=cosxR[-2,0]偶函数2π思考交流:≥解:1.函数f(x)=cos4x,x∈R是( )
A.最小正周期为π的偶函数
B.最小正周期为π的奇函数
C.最小正周期为 的偶函数
D.最小正周期为 的奇函数C2.下列函数,在[ ,π]上增加的是( )
A.y=cos2x B.y=cosx
C.y=sin2x D.y=sinxA3.不求值比较下列两个三角函数值的大小.解:>4.对于实数范围内的x,分别写出满足sinx=cosx,sinx>cosx,sinx
——雨果
