1.7.3 正切函数的诱导公式 课件
文档属性
| 名称 | 1.7.3 正切函数的诱导公式 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览





文档简介
课件17张PPT。1.7.3 正切函数的诱导公式 同学们已经知道,在正、余弦函数中,我们是先学诱导公式,再学图像与性质的. 在学正切函数时,我们先学图像与性质,再学诱导公式,本节课我们来学习正切函数的诱导公式.1.会推导正切函数的诱导公式.(重点)
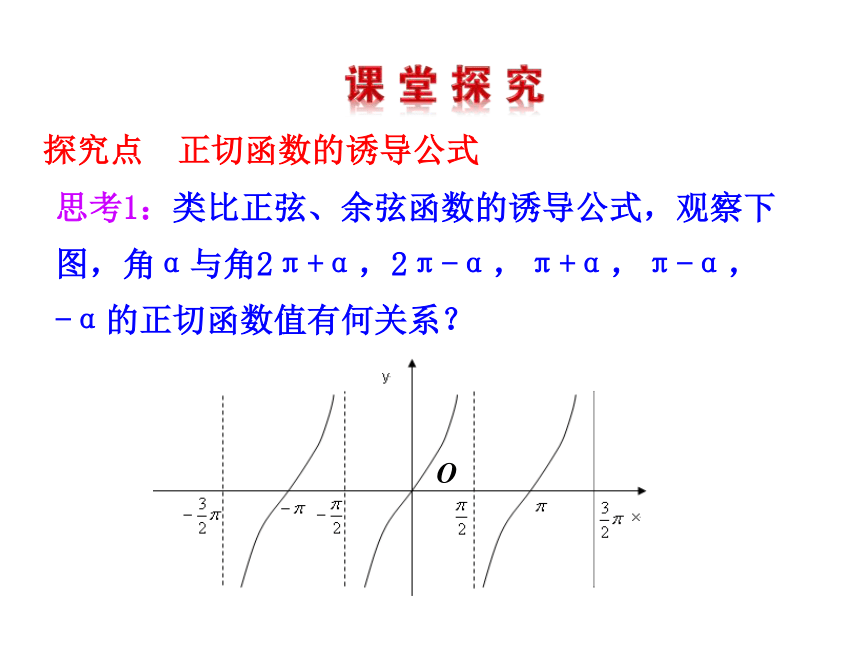
2.熟练掌握正切函数的诱导公式,并能根据公式解决化简、求值等问题.(难点)思考1:类比正弦、余弦函数的诱导公式,观察下图,角α与角2π+α,2π-α,π+α,π-α,
-α的正切函数值有何关系? O探究点 正切函数的诱导公式我们可以归纳出以下公式: 正切函数的诱导公式tan(2π+α)=tanα tan(-α)=-tanαtan(2π-α)=-tanαtan(π-α)=-tanαtan(π+α)=tanα其中角α是任意角这些公式都叫作正切函数的诱导公式 提示: 的三角函数值等于
α的同名函数值,再放上原函数的象限符号. 简
化成“函数名不变,符号看象限”的口诀.思考2:以上公式都叫作正切函数的诱导公式,它
们分别反映了 的三角函数与
α的三角函数之间的关系,你能概括一下这四组
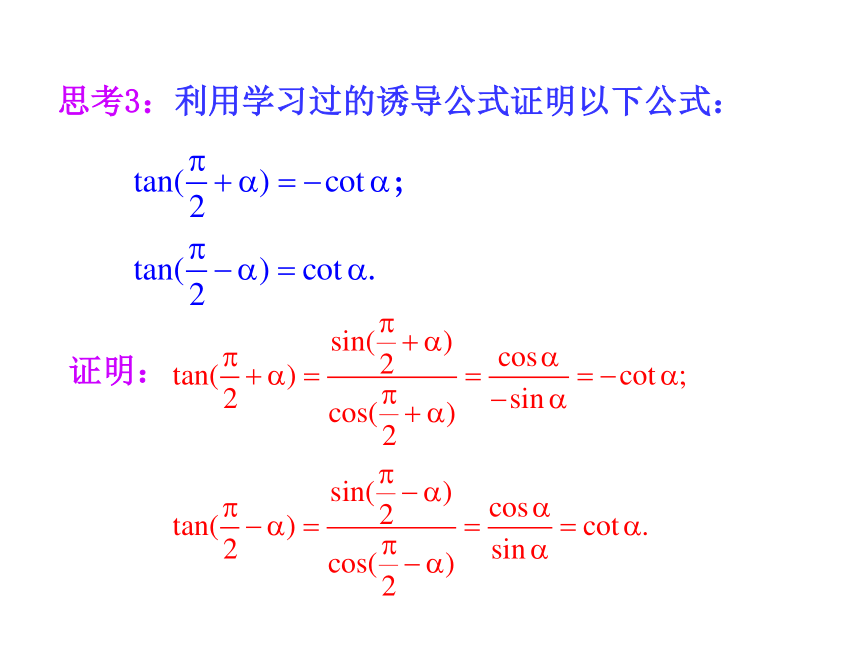
公式的共同特点和规律吗?思考3:利用学习过的诱导公式证明以下公式:证明:以上两组诱导公式口诀:“函数名改变,符号看象限.”任意角的三角函数0~2π的角的三角函数锐角的三角函数参考下面的框图,想想每次变换应该运用哪些公式?α±2kππ±α【思考探究】 由此可知,我们可以利用诱导公式,将任意角的三角函数问题转化为锐角的三角函数问题.
思考:如何应用正切函数的诱导公式进行求值、化简和证明?
提示:先用-α的诱导公式化为正角的三角函数值,再用2kπ+α(k∈Z)的诱导公式化为[0,2π)内的三角函数值,再用π+α,π-α,2π-α的诱导公式化为锐角的三角函数值,即采用化负为正,化大为小的方法.解:在利用公式进行化简时,一定要注意公式变形时符号及函数名称是否变化.2.已知tanx<0,则x的取值范围为__________________________. 3. 已知tanx=-1,则x的值为_____________________.4.求值:正切函数的诱导公式 tanαtan α-tan α-tan αtan α函数名不变
符号看象限 函数名改变
符号看象限 -cot αcot α其中符号看象限指的是将α看成锐角时,原三角函数的符号是“+”还是“-”.重要的不是知识的数量,而是知识的质量,有些人知道很多很多,但却不知道最有用的东西.
——列夫?托尔斯泰
2.熟练掌握正切函数的诱导公式,并能根据公式解决化简、求值等问题.(难点)思考1:类比正弦、余弦函数的诱导公式,观察下图,角α与角2π+α,2π-α,π+α,π-α,
-α的正切函数值有何关系? O探究点 正切函数的诱导公式我们可以归纳出以下公式: 正切函数的诱导公式tan(2π+α)=tanα tan(-α)=-tanαtan(2π-α)=-tanαtan(π-α)=-tanαtan(π+α)=tanα其中角α是任意角这些公式都叫作正切函数的诱导公式 提示: 的三角函数值等于
α的同名函数值,再放上原函数的象限符号. 简
化成“函数名不变,符号看象限”的口诀.思考2:以上公式都叫作正切函数的诱导公式,它
们分别反映了 的三角函数与
α的三角函数之间的关系,你能概括一下这四组
公式的共同特点和规律吗?思考3:利用学习过的诱导公式证明以下公式:证明:以上两组诱导公式口诀:“函数名改变,符号看象限.”任意角的三角函数0~2π的角的三角函数锐角的三角函数参考下面的框图,想想每次变换应该运用哪些公式?α±2kππ±α【思考探究】 由此可知,我们可以利用诱导公式,将任意角的三角函数问题转化为锐角的三角函数问题.
思考:如何应用正切函数的诱导公式进行求值、化简和证明?
提示:先用-α的诱导公式化为正角的三角函数值,再用2kπ+α(k∈Z)的诱导公式化为[0,2π)内的三角函数值,再用π+α,π-α,2π-α的诱导公式化为锐角的三角函数值,即采用化负为正,化大为小的方法.解:在利用公式进行化简时,一定要注意公式变形时符号及函数名称是否变化.2.已知tanx<0,则x的取值范围为__________________________. 3. 已知tanx=-1,则x的值为_____________________.4.求值:正切函数的诱导公式 tanαtan α-tan α-tan αtan α函数名不变
符号看象限 函数名改变
符号看象限 -cot αcot α其中符号看象限指的是将α看成锐角时,原三角函数的符号是“+”还是“-”.重要的不是知识的数量,而是知识的质量,有些人知道很多很多,但却不知道最有用的东西.
——列夫?托尔斯泰
