2.1 从位移、速度、力到向量 课件3
图片预览









文档简介
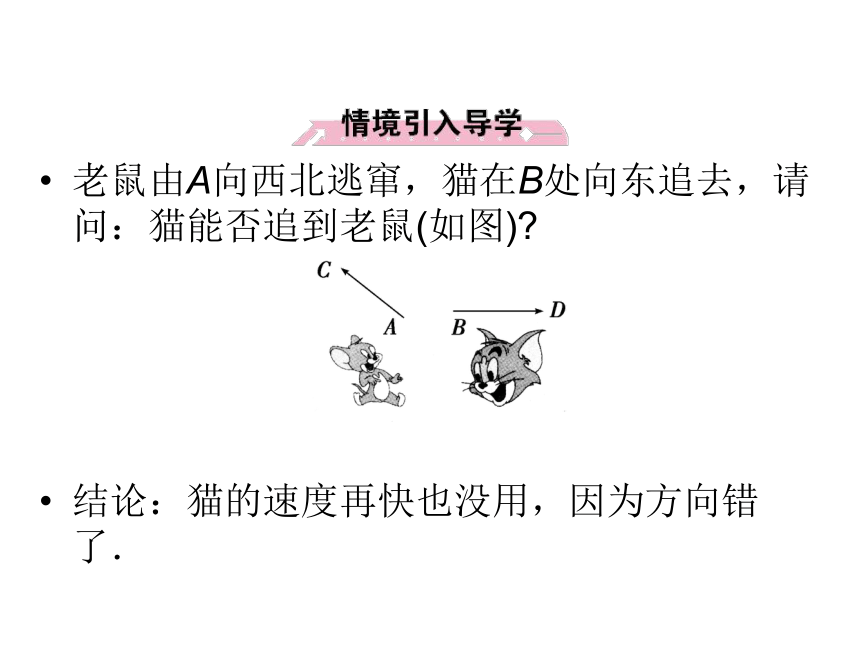
课件43张PPT。平面向量第二章2.1 从位移、速度、力到向量第二章老鼠由A向西北逃窜,猫在B处向东追去,请问:猫能否追到老鼠(如图)?
结论:猫的速度再快也没用,因为方向错了.
分析:老鼠逃窜的路线AC、猫追逐的路线BD实际上都是有长短、有方向的量.
生活中还有许多既有大小又有方向的量,你能说出它们并指出其大小和方向吗?本节就来学习这方面的知识.大小 方向 方向和长度 有向线段 向量的大小 向量的方向 |a| 4.四种重要的向量
(1)长度为零的向量叫作________,记作_____或______,它的方向与任一向量平行.
(2)与向量a________,且长度为________的向量,叫作a方向上的单位向量,记作________.
(3)长度________且方向________的向量叫作相等向量,向量a与b相等,记作a=b.规定所有的零向量________.
(4)如果表示两个向量的有向线段所在的直线__________,则称这两个向量________或________,a与b平行或共线,记作a∥b.零向量 0 同方向 单位1 a0 相等 相同 相等 平行或重合 平行 共线 1.下列各量:①密度;②浮力;③温度;④风速.其中向量有( )
A.①② B.②③
C.②④ D.③④
[答案] C
[解析] 主要考查向量与数量的区别.
由向量的概念可知:浮力和风速是向量,密度与温度是数量,故选C.
实际问题中的一些量(温度、电量等),尽管它们有正、负之分,但不是表示方向的,它们是数量,而向量是一个既有大小又有方向的量,如位移、速度、加速度、力等物理量.[答案] D3.下列说法中正确的是( )
A.只有方向相同或相反的向量是平行向量
B.零向量的长度是零
C.长度相等的两个向量是相等的向量
D.共线向量是在一条直线上的向量
[答案] B
[解析] 表示向量的有向线段所在的直线平行或重合,这样的向量都是平行向量.长度和方向都相同的向量才是相等的向量,选项B正确.
4.若对任意向量b,均有a∥b,则a为________.
[答案] 0
[解析] 零向量可以与任意向量平行.
[答案] ②向量的有关概念 [思路分析] 本题涉及了向量的几个重要概念.解答时可从向量定义、向量的模、相等向量、平行向量等概念入手,逐一判断对错.
[答案] (4)
[规律总结] 对于一些意义相近的概念,一定要准确把握,仔细分辨.如有向线段与向量,不能混同,有向线段是向量的几何表现形式,不仅有大小和方向,还有起点和终点,而向量只有大小和方向.比如向量a的单位向量有两个,这两个单位向量方向相反.再如向量共线与向量同向,共线不一定同向,但同向一定共线.[答案] C相等向量与共线向量 [思路分析] (1)要找出具体相等向量,只需在正方形ABCD中分别找出长度相等且方向相同的向量即可;
(2)共线向量只需找方向相同或相反的向量即可.[规范解答] (1)作出图形如图,由已知,有|a|=|c|=|e|=|g|=1,
[规律总结] (1)寻找相等向量要把握住向量的两要素:大小和方向,相等向量必须二者都相同才成立.同时,也可以看出,向量是可以平移的,相等向量的起点并不一定要相同.
(2)对于非零向量,共线向量只需把握向量的方向要素,与向量的大小无关,故寻找非零共线向量时,只需判断两向量所在的直线是否共线或者重合即可.如图,在正六边形ABCDEF中,O为中心.向量表示的模型 [思路分析] 首先确立指向标,然后再根据行驶方向和距离作出向量,进而求解.[规范解答] (1)如图所示.
[规律总结] (1)准确画出向量的方法是先确定向量起点,再确定向量的方向,然后根据向量的大小确定向量的终点.
(2)要能够运用向量的观点将实际问题抽象成数学模型,“数学建模”是今后能力培养的主要方向,需要在日常学习中不断积累经验.[解析] 如图所示,A、B、C、D分别表示甲地、乙地、丙地、丁地,依题意知,△ABC为正三角形,向量的应用 [思路分析] 当赛车总共转了360°之后,回到起点时,位移刚好是零.
[规律总结] 向量相等或共线与表示向量的有向线段的起点无关,仅决定于向量的长度和方向.[答案] 菱形[错解] D[辨析] 认为①正确是忽略了0和0的区别.由|a|=0可知a是零向量,但是a≠0,之所以出现这样的错误.原因是对零向量的概念认识不清;认为②正确是把两个向量的模相等和两个实数相等混淆了,两个向量的模相等,只能说明它们的长度相等,并不意味着它们的方向是相同或相反的;认为③正确是因为对两个向量平行的意义理解不透造成的,两个向量平行,可以得到它们的方向相同或相反,而未必得到它们的模相等,④正确.
[正解] A
结论:猫的速度再快也没用,因为方向错了.
分析:老鼠逃窜的路线AC、猫追逐的路线BD实际上都是有长短、有方向的量.
生活中还有许多既有大小又有方向的量,你能说出它们并指出其大小和方向吗?本节就来学习这方面的知识.大小 方向 方向和长度 有向线段 向量的大小 向量的方向 |a| 4.四种重要的向量
(1)长度为零的向量叫作________,记作_____或______,它的方向与任一向量平行.
(2)与向量a________,且长度为________的向量,叫作a方向上的单位向量,记作________.
(3)长度________且方向________的向量叫作相等向量,向量a与b相等,记作a=b.规定所有的零向量________.
(4)如果表示两个向量的有向线段所在的直线__________,则称这两个向量________或________,a与b平行或共线,记作a∥b.零向量 0 同方向 单位1 a0 相等 相同 相等 平行或重合 平行 共线 1.下列各量:①密度;②浮力;③温度;④风速.其中向量有( )
A.①② B.②③
C.②④ D.③④
[答案] C
[解析] 主要考查向量与数量的区别.
由向量的概念可知:浮力和风速是向量,密度与温度是数量,故选C.
实际问题中的一些量(温度、电量等),尽管它们有正、负之分,但不是表示方向的,它们是数量,而向量是一个既有大小又有方向的量,如位移、速度、加速度、力等物理量.[答案] D3.下列说法中正确的是( )
A.只有方向相同或相反的向量是平行向量
B.零向量的长度是零
C.长度相等的两个向量是相等的向量
D.共线向量是在一条直线上的向量
[答案] B
[解析] 表示向量的有向线段所在的直线平行或重合,这样的向量都是平行向量.长度和方向都相同的向量才是相等的向量,选项B正确.
4.若对任意向量b,均有a∥b,则a为________.
[答案] 0
[解析] 零向量可以与任意向量平行.
[答案] ②向量的有关概念 [思路分析] 本题涉及了向量的几个重要概念.解答时可从向量定义、向量的模、相等向量、平行向量等概念入手,逐一判断对错.
[答案] (4)
[规律总结] 对于一些意义相近的概念,一定要准确把握,仔细分辨.如有向线段与向量,不能混同,有向线段是向量的几何表现形式,不仅有大小和方向,还有起点和终点,而向量只有大小和方向.比如向量a的单位向量有两个,这两个单位向量方向相反.再如向量共线与向量同向,共线不一定同向,但同向一定共线.[答案] C相等向量与共线向量 [思路分析] (1)要找出具体相等向量,只需在正方形ABCD中分别找出长度相等且方向相同的向量即可;
(2)共线向量只需找方向相同或相反的向量即可.[规范解答] (1)作出图形如图,由已知,有|a|=|c|=|e|=|g|=1,
[规律总结] (1)寻找相等向量要把握住向量的两要素:大小和方向,相等向量必须二者都相同才成立.同时,也可以看出,向量是可以平移的,相等向量的起点并不一定要相同.
(2)对于非零向量,共线向量只需把握向量的方向要素,与向量的大小无关,故寻找非零共线向量时,只需判断两向量所在的直线是否共线或者重合即可.如图,在正六边形ABCDEF中,O为中心.向量表示的模型 [思路分析] 首先确立指向标,然后再根据行驶方向和距离作出向量,进而求解.[规范解答] (1)如图所示.
[规律总结] (1)准确画出向量的方法是先确定向量起点,再确定向量的方向,然后根据向量的大小确定向量的终点.
(2)要能够运用向量的观点将实际问题抽象成数学模型,“数学建模”是今后能力培养的主要方向,需要在日常学习中不断积累经验.[解析] 如图所示,A、B、C、D分别表示甲地、乙地、丙地、丁地,依题意知,△ABC为正三角形,向量的应用 [思路分析] 当赛车总共转了360°之后,回到起点时,位移刚好是零.
[规律总结] 向量相等或共线与表示向量的有向线段的起点无关,仅决定于向量的长度和方向.[答案] 菱形[错解] D[辨析] 认为①正确是忽略了0和0的区别.由|a|=0可知a是零向量,但是a≠0,之所以出现这样的错误.原因是对零向量的概念认识不清;认为②正确是把两个向量的模相等和两个实数相等混淆了,两个向量的模相等,只能说明它们的长度相等,并不意味着它们的方向是相同或相反的;认为③正确是因为对两个向量平行的意义理解不透造成的,两个向量平行,可以得到它们的方向相同或相反,而未必得到它们的模相等,④正确.
[正解] A
