2.1 从位移、速度、力到向量 课件4
文档属性
| 名称 | 2.1 从位移、速度、力到向量 课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 464.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 10:41:03 | ||
图片预览







文档简介
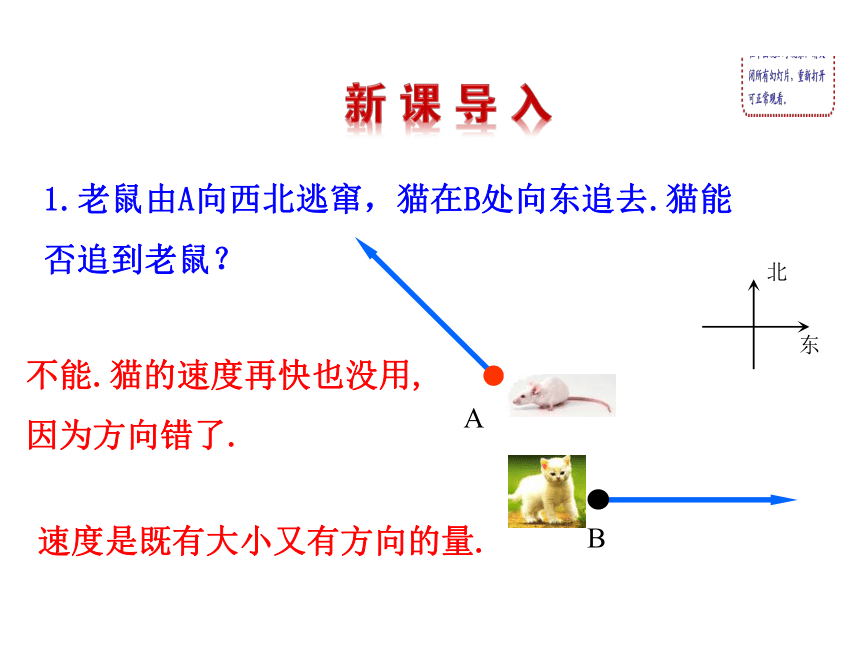
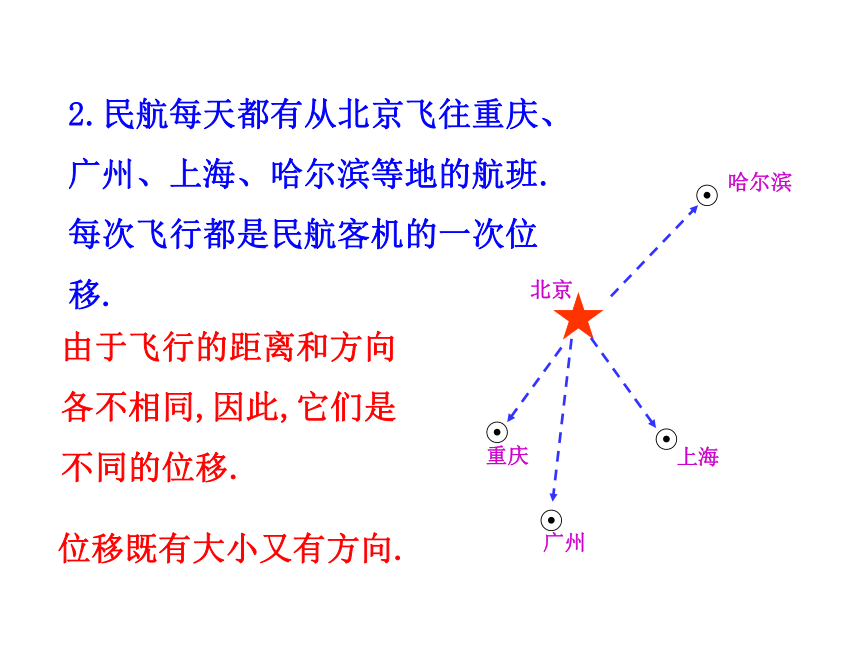
课件24张PPT。2.1 从位移、速度、力到向量1.老鼠由A向西北逃窜,猫在B处向东追去.猫能否追到老鼠?不能.猫的速度再快也没用, 因为方向错了. 速度是既有大小又有方向的量.北东北京广州上海哈尔滨重庆2.民航每天都有从北京飞往重庆、广州、上海、哈尔滨等地的航班.每次飞行都是民航客机的一次位移.由于飞行的距离和方向各不相同,因此,它们是不同的位移.位移既有大小又有方向.3.假如学校位于你家东偏北30°方向,距离你家
2 000 m.从家到学校,可能有长短不同的几条路.
无论走哪条路,你的位移都是向东偏北30°方向
移动了2 000 m.4.飞机向东北方向飞行了150 km,飞行时间为半小时,飞行速度的大小是300 km/h,方向是东北.5.某著名运动员投掷标枪时,标枪的初始速度的记录资料是:平均出手角度θ=43.242°,平均出手速度大小为v=28.35 m/s.6.起重机吊装物体时,物体既受到竖直向下的重力作用,同时又受到竖直向上的起重机拉力的作用.当拉力的大小超过重力的大小时,物体即被吊起.思考:物理中,既有大小又有方向的量,叫作什么?在数学中,既有大小又有方向的量又叫作什么呢?提示:矢量,向量.1.理解向量、零向量、单位向量、相等向量的定义,并能用数学符号表示向量.(重点)
2. 理解向量的几何表示,并会用字母表示向量.(重点)
3.掌握向量的模、相等向量、平行(共线)向量的概念,并能在图形中辨认相等向量、平行(共线)向量. (难点)既有大小,又有方向的量统称为向量.
问题1.现实生活中有哪些量既有大小又有方向?
提示:力、加速度、动量、电场强度等.
问题2.哪些量只有大小没有方向?
提示:距离、身高、质量、时间、面积等.探究点1 向量的概念 注意:数量与向量的区别
1.数量只有大小,是一个数,可以进行代数运算、
能比较大小.
2.向量不仅有大小还有方向,具有双重性,
不能比较大小. 有向线段——具有方向和长度的线段.
___________长度表示向量的大小,
_____所指的方向表示向量的方向.探究点2 向量的表示方法1.几何表示法:有向线段.如图:以A为起点、B为终点的有向线段记作 回顾物理中表示位移、速度、力的方法,思考向量可以用什么表示?有向线段的箭头2.字母表示法: 用 等小写字母表示.提示:有区别:矢量一般是指物理中的既有大小又有方向的量,与起点位置有关.而在数学中我们研究的是仅由大小和方向确定,与起点位置无关的向量,也称为自由向量.想一想:矢量和向量都是既有大小又有方向的量,都
可以用有向线段表示,是不是就可以说这二者
是相同的呢?探究点3 向量的模问题:长度为0的向量是什么样的向量?长度为1的向量呢?向量 (或 )的大小,即长度(也称模).注:零向量,单位向量都是只限制大小,不确定方向的.记作: 或(| |).思考:平面直角坐标系内,起点在原点的单位向量,
它们终点的轨迹是什么图形?提示:如图,轨迹是以O为圆心,半径为1的圆(单位圆).oxy探究点4 向量平行与相等向量如果表示两个向量的有向线段所在的直线平行或重合,则称这两个向量平行或共线.1.向量平行 记作:规定:零向量与任一向量平行.即对于任意向量 ,
都有长度相等且方向相同的向量,叫作相等向量.规定: 零向量与零向量相等.2.相等向量想一想:1.相等向量一定平行吗? 2.平行的向量一定是相等向量吗?是不是若向量 与 相等,记作:思考1 共线向量和相等向量有什么关系?
提示:共线向量不一定是相等向量;相等向量一定
是共线向量.
思考2 若两个向量在同一直线上,则这两个向量
有什么关系?
提示:平行.(2)在以A,B,C,D,E,F为起点或终点的向量中,与
向量 共线的向量有:例.如图,D,E,F依次是等边三角形ABC的边AB,BC,AC的中点,在以A,B,C,D,E,F为起点或终点的向量中,
(1)找出与向量 相等的向量.
(2)找出与向量 共线的向量.解:由三角形中位线定理不难得到:
(1)在以A,B,C,D,E,F为起点
或终点的向量中,与向量 相等的向量有:11个变式练习 如图,设O是正六边形ABCDEF的中心,
(1)写出图中与向量 相等的向量.(3)是否存在与向量 长度相等,方向相反的向量?存在,为(4)与向量 长度相等且共线的向量有哪些?(2)与向量 长度相等的向量有多少 个?1.A .2 B .3 C. 4 D. 5B2.设O是正方形ABCD的中心,向量 ???????????
??
是 ( )
A.平行向量 B.有相同终点的向量
C.相等向量 D.模相等的向量D3.右图中的向量是什么关系?说明:
任意两个非零相等向量可用同一条有向线段表示,与有向线段的起点无关.解析:相等的有7个.长度相等且共线的有15个.BA4.在4×5的方格纸中有一个向量 ,以图中的格点为起
点和终点作向量,其中与 相等的向量有多少个?与
长度相等且共线的向量有多少个?( 除外)3.零向量、单位向量的概念.2.向量的长度(向量的模).1.向量的概念及表示方法.4.向量平行(共线)与相等向量.本节课主要学习了:当你还不能对自己说今天学到了什么东西时,你就不要去睡觉.
——利希顿堡
2 000 m.从家到学校,可能有长短不同的几条路.
无论走哪条路,你的位移都是向东偏北30°方向
移动了2 000 m.4.飞机向东北方向飞行了150 km,飞行时间为半小时,飞行速度的大小是300 km/h,方向是东北.5.某著名运动员投掷标枪时,标枪的初始速度的记录资料是:平均出手角度θ=43.242°,平均出手速度大小为v=28.35 m/s.6.起重机吊装物体时,物体既受到竖直向下的重力作用,同时又受到竖直向上的起重机拉力的作用.当拉力的大小超过重力的大小时,物体即被吊起.思考:物理中,既有大小又有方向的量,叫作什么?在数学中,既有大小又有方向的量又叫作什么呢?提示:矢量,向量.1.理解向量、零向量、单位向量、相等向量的定义,并能用数学符号表示向量.(重点)
2. 理解向量的几何表示,并会用字母表示向量.(重点)
3.掌握向量的模、相等向量、平行(共线)向量的概念,并能在图形中辨认相等向量、平行(共线)向量. (难点)既有大小,又有方向的量统称为向量.
问题1.现实生活中有哪些量既有大小又有方向?
提示:力、加速度、动量、电场强度等.
问题2.哪些量只有大小没有方向?
提示:距离、身高、质量、时间、面积等.探究点1 向量的概念 注意:数量与向量的区别
1.数量只有大小,是一个数,可以进行代数运算、
能比较大小.
2.向量不仅有大小还有方向,具有双重性,
不能比较大小. 有向线段——具有方向和长度的线段.
___________长度表示向量的大小,
_____所指的方向表示向量的方向.探究点2 向量的表示方法1.几何表示法:有向线段.如图:以A为起点、B为终点的有向线段记作 回顾物理中表示位移、速度、力的方法,思考向量可以用什么表示?有向线段的箭头2.字母表示法: 用 等小写字母表示.提示:有区别:矢量一般是指物理中的既有大小又有方向的量,与起点位置有关.而在数学中我们研究的是仅由大小和方向确定,与起点位置无关的向量,也称为自由向量.想一想:矢量和向量都是既有大小又有方向的量,都
可以用有向线段表示,是不是就可以说这二者
是相同的呢?探究点3 向量的模问题:长度为0的向量是什么样的向量?长度为1的向量呢?向量 (或 )的大小,即长度(也称模).注:零向量,单位向量都是只限制大小,不确定方向的.记作: 或(| |).思考:平面直角坐标系内,起点在原点的单位向量,
它们终点的轨迹是什么图形?提示:如图,轨迹是以O为圆心,半径为1的圆(单位圆).oxy探究点4 向量平行与相等向量如果表示两个向量的有向线段所在的直线平行或重合,则称这两个向量平行或共线.1.向量平行 记作:规定:零向量与任一向量平行.即对于任意向量 ,
都有长度相等且方向相同的向量,叫作相等向量.规定: 零向量与零向量相等.2.相等向量想一想:1.相等向量一定平行吗? 2.平行的向量一定是相等向量吗?是不是若向量 与 相等,记作:思考1 共线向量和相等向量有什么关系?
提示:共线向量不一定是相等向量;相等向量一定
是共线向量.
思考2 若两个向量在同一直线上,则这两个向量
有什么关系?
提示:平行.(2)在以A,B,C,D,E,F为起点或终点的向量中,与
向量 共线的向量有:例.如图,D,E,F依次是等边三角形ABC的边AB,BC,AC的中点,在以A,B,C,D,E,F为起点或终点的向量中,
(1)找出与向量 相等的向量.
(2)找出与向量 共线的向量.解:由三角形中位线定理不难得到:
(1)在以A,B,C,D,E,F为起点
或终点的向量中,与向量 相等的向量有:11个变式练习 如图,设O是正六边形ABCDEF的中心,
(1)写出图中与向量 相等的向量.(3)是否存在与向量 长度相等,方向相反的向量?存在,为(4)与向量 长度相等且共线的向量有哪些?(2)与向量 长度相等的向量有多少 个?1.A .2 B .3 C. 4 D. 5B2.设O是正方形ABCD的中心,向量 ???????????
??
是 ( )
A.平行向量 B.有相同终点的向量
C.相等向量 D.模相等的向量D3.右图中的向量是什么关系?说明:
任意两个非零相等向量可用同一条有向线段表示,与有向线段的起点无关.解析:相等的有7个.长度相等且共线的有15个.BA4.在4×5的方格纸中有一个向量 ,以图中的格点为起
点和终点作向量,其中与 相等的向量有多少个?与
长度相等且共线的向量有多少个?( 除外)3.零向量、单位向量的概念.2.向量的长度(向量的模).1.向量的概念及表示方法.4.向量平行(共线)与相等向量.本节课主要学习了:当你还不能对自己说今天学到了什么东西时,你就不要去睡觉.
——利希顿堡
