2.2.1 向量的加法 课件
图片预览




文档简介
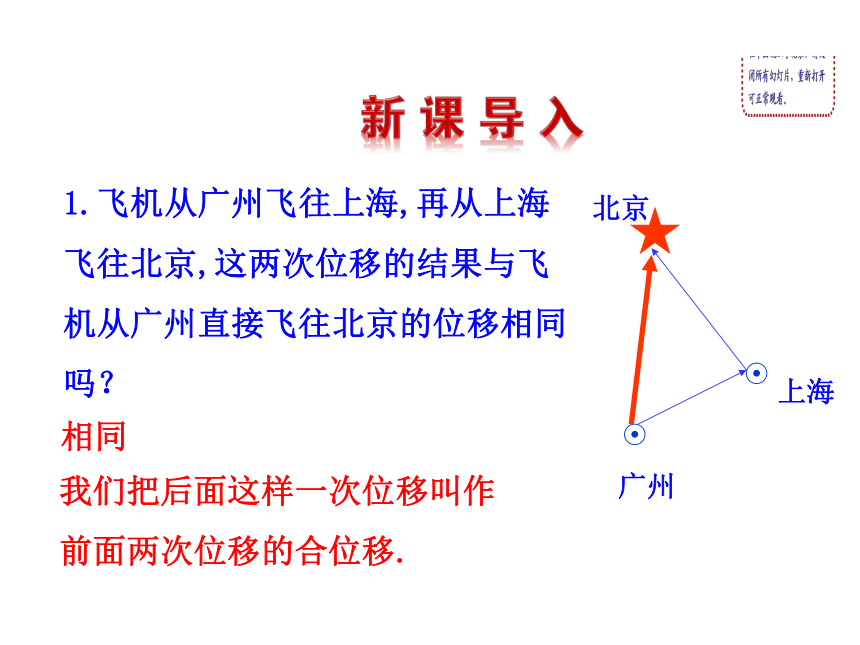
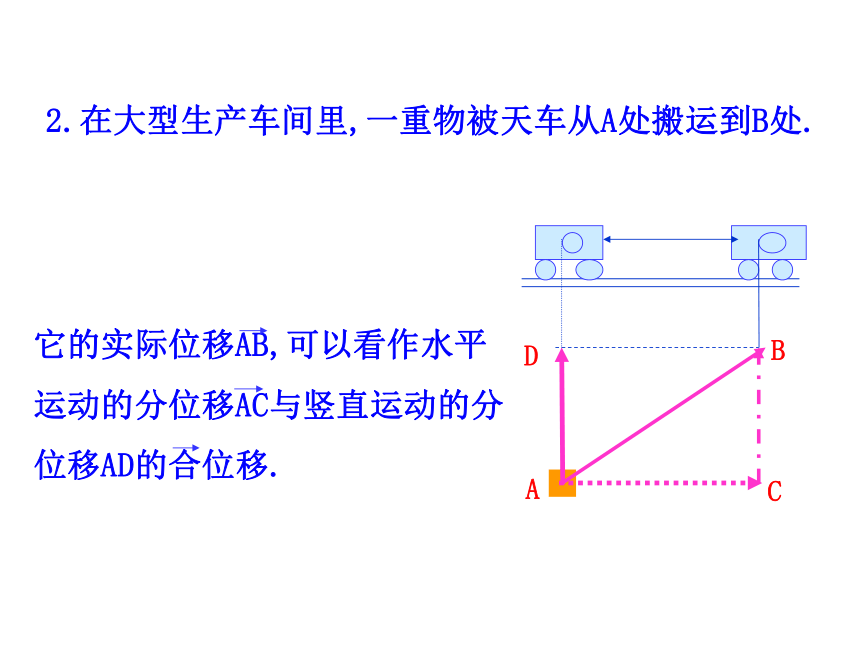
课件23张PPT。2.2.1 向量的加法北京广州上海1.飞机从广州飞往上海,再从上海飞往北京,这两次位移的结果与飞机从广州直接飞往北京的位移相同吗?我们把后面这样一次位移叫作前面两次位移的合位移.相同ABCD2.在大型生产车间里,一重物被天车从A处搬运到B处.由分位移求合位移,称为位移的合成.
在上一节课中我们知道位移是向量,因此位移合成就是向量的加法,那么向量的加法怎么体现?符合哪些规律呢?这就是我们今天要探究的内容.1.掌握向量加法的概念;能熟练运用三角形法则和平行四边形法则求几个向量的和向量.(重点)2.能准确表述向量加法的交换律和结合律,并能熟练运用它们进行向量计算. (重点)
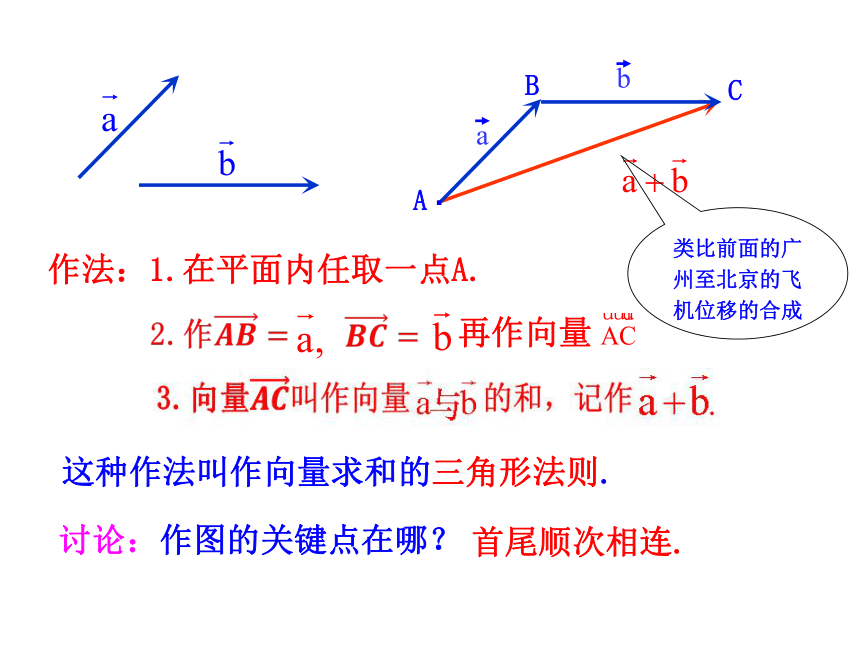
3.向量加法的概念和向量加法的法则及运算律.(难点)既然向量的加法可以类比位移的合成,想一想,求两个向量的和是否也可以类比前面位移的合成呢?探究点1 向量加法的三角形法则如下图,已知向量 如何求这两向量的和?这种作法叫作向量求和的三角形法则.AC作法:1.在平面内任取一点A.讨论:作图的关键点在哪?首尾顺次相连.Bab类比前面的广州至北京的飞机位移的合成
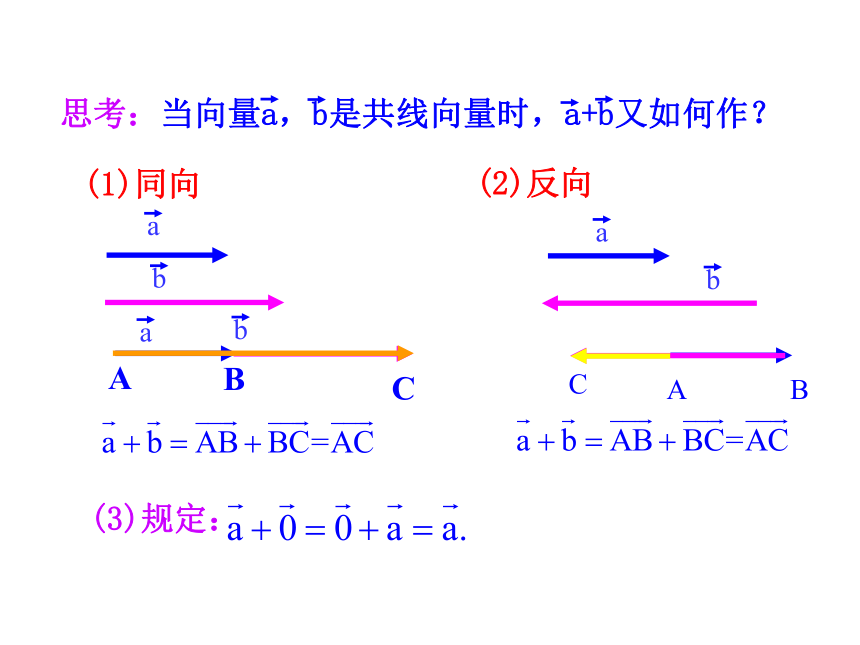
再作向量.(1)同向(2)反向aab思考:当向量a,b是共线向量时,a+b又如何作?(3)规定:探究点2 向量加法的平行四边形法则
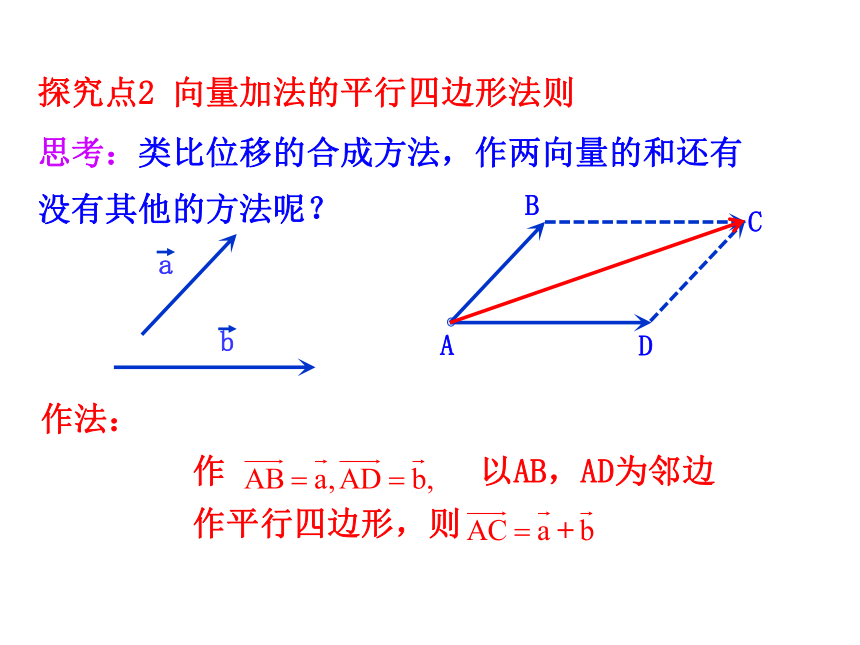
思考:类比位移的合成方法,作两向量的和还有没有其他的方法呢?BDC作法:
作 以AB,AD为邻边
作平行四边形,则上述这种方法叫作向量求和的平行四边形法则.思考:这种方法的作图关键点是什么呢?提示:共起点.提升总结:三角形法则和平行四边形法则的使用范围.
(1)三角形法则适用于任意两个向量的加法;
(2)平行四边形法则适用于不共线的两个向量的加法.例1 轮船从A港沿东偏北 30°方向行驶了40 n mile
(海里)到达 B 处,再由B处沿正北方向行驶40 n mile
到达 C 处.求此时轮船与A港的相对位置.北AB东C东北ABC因为答: 轮船此时位于A港东偏北
60°,且距A港40 n mile 的
C处.探究点3 向量加法的运算律
数的加法满足交换律与结合律 ,即对任意a,b∈R,有a+b=b+a,(a+b)+c=a+(b+c).任意向量 的加法是否也满足交换律和结合律?向量的加法满足交换律和结合律?DACB???A?BC??D??思考:能否将它推广至多个向量的求和?A1A2A3A1A2+A2A3= _______多边形法则:n个首尾顺次相接的向量的和等于折线起点到终点的向量.解:如图, 表示 , 表示 .以OA,OB为邻边作□OACB,则 表示合力 .
在Rt△OAC中, =40N,
=30N.由勾股定理得例2 两个力 和 同时作用在一个物体上,其中 的大小
为40 N,方向向东, 的大小为30 N,方向向北,求它们的合力.东北OθCAB设合力 与力 的夹角为θ,则
所以θ≈37°.
答:合力大小为50N,方向为东偏北37°.OB例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1=3.46 km/h,河水流动的速度v2=2.0 km/h.试求小船过河实际航行速度的大小和方向. v1v2解:如图,设 表示小船垂直于河
岸行驶的速度, 表示水流的速度,
以OA,OB为邻边作□OABC,则 就
是小船实际航行的速度.CAABCDEF1.如图,在正六边形ABCDEF中, ( )
A. B. C. D. D2.下列非零向量的运算结果为零向量的是( )
A.
B.
C.
D.D3.试用向量方法证明:对角线互相平分的四边形必是平行四边形.证明结论得证.因为3.向量加法运算律.1.向量加法的三角形法则(首尾相接).2.向量加法的平行四边形法则(起点相同).??4.三角形法则推广为多边形法则长期的心灰意懒以及烦恼足以致人于贫病枯萎.
——布朗
在上一节课中我们知道位移是向量,因此位移合成就是向量的加法,那么向量的加法怎么体现?符合哪些规律呢?这就是我们今天要探究的内容.1.掌握向量加法的概念;能熟练运用三角形法则和平行四边形法则求几个向量的和向量.(重点)2.能准确表述向量加法的交换律和结合律,并能熟练运用它们进行向量计算. (重点)
3.向量加法的概念和向量加法的法则及运算律.(难点)既然向量的加法可以类比位移的合成,想一想,求两个向量的和是否也可以类比前面位移的合成呢?探究点1 向量加法的三角形法则如下图,已知向量 如何求这两向量的和?这种作法叫作向量求和的三角形法则.AC作法:1.在平面内任取一点A.讨论:作图的关键点在哪?首尾顺次相连.Bab类比前面的广州至北京的飞机位移的合成
再作向量.(1)同向(2)反向aab思考:当向量a,b是共线向量时,a+b又如何作?(3)规定:探究点2 向量加法的平行四边形法则
思考:类比位移的合成方法,作两向量的和还有没有其他的方法呢?BDC作法:
作 以AB,AD为邻边
作平行四边形,则上述这种方法叫作向量求和的平行四边形法则.思考:这种方法的作图关键点是什么呢?提示:共起点.提升总结:三角形法则和平行四边形法则的使用范围.
(1)三角形法则适用于任意两个向量的加法;
(2)平行四边形法则适用于不共线的两个向量的加法.例1 轮船从A港沿东偏北 30°方向行驶了40 n mile
(海里)到达 B 处,再由B处沿正北方向行驶40 n mile
到达 C 处.求此时轮船与A港的相对位置.北AB东C东北ABC因为答: 轮船此时位于A港东偏北
60°,且距A港40 n mile 的
C处.探究点3 向量加法的运算律
数的加法满足交换律与结合律 ,即对任意a,b∈R,有a+b=b+a,(a+b)+c=a+(b+c).任意向量 的加法是否也满足交换律和结合律?向量的加法满足交换律和结合律?DACB???A?BC??D??思考:能否将它推广至多个向量的求和?A1A2A3A1A2+A2A3= _______多边形法则:n个首尾顺次相接的向量的和等于折线起点到终点的向量.解:如图, 表示 , 表示 .以OA,OB为邻边作□OACB,则 表示合力 .
在Rt△OAC中, =40N,
=30N.由勾股定理得例2 两个力 和 同时作用在一个物体上,其中 的大小
为40 N,方向向东, 的大小为30 N,方向向北,求它们的合力.东北OθCAB设合力 与力 的夹角为θ,则
所以θ≈37°.
答:合力大小为50N,方向为东偏北37°.OB例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1=3.46 km/h,河水流动的速度v2=2.0 km/h.试求小船过河实际航行速度的大小和方向. v1v2解:如图,设 表示小船垂直于河
岸行驶的速度, 表示水流的速度,
以OA,OB为邻边作□OABC,则 就
是小船实际航行的速度.CAABCDEF1.如图,在正六边形ABCDEF中, ( )
A. B. C. D. D2.下列非零向量的运算结果为零向量的是( )
A.
B.
C.
D.D3.试用向量方法证明:对角线互相平分的四边形必是平行四边形.证明结论得证.因为3.向量加法运算律.1.向量加法的三角形法则(首尾相接).2.向量加法的平行四边形法则(起点相同).??4.三角形法则推广为多边形法则长期的心灰意懒以及烦恼足以致人于贫病枯萎.
——布朗
