2.4.1-2.4.2 平面向量的坐标表示 课件3
文档属性
| 名称 | 2.4.1-2.4.2 平面向量的坐标表示 课件3 |
|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览











文档简介
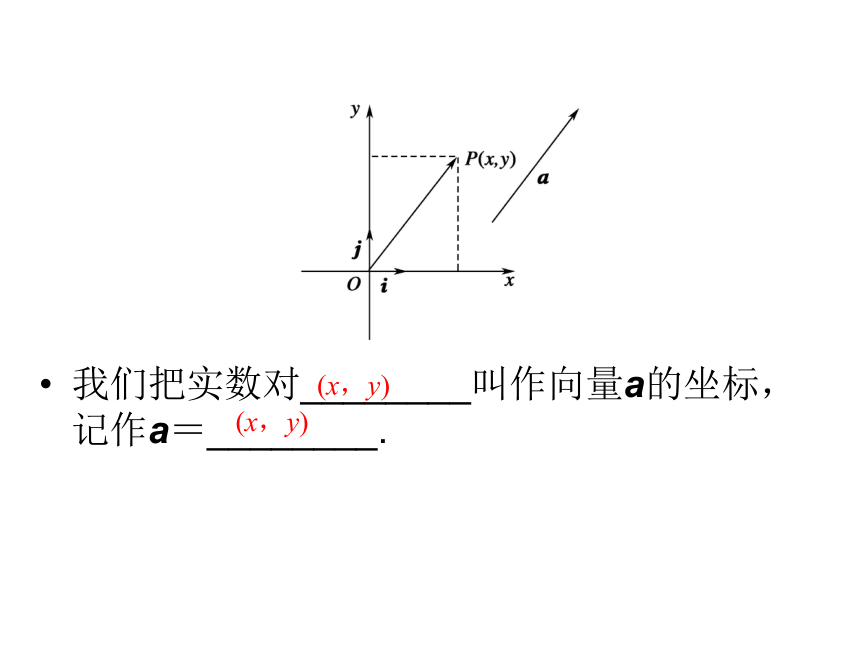
课件44张PPT。平面向量第二章2.4.1-2.4.2 平面向量的坐标表示第二章我们把实数对________叫作向量a的坐标,记作a=________.(x,y) (x,y) (x1+x2,y1+y2) (x1-x2,y1-y2) 和与差 (λx,λy) 实数与向量相应坐标 (x2-x1,y2-y1) 终点的相应坐标 始点的相应坐标x1y2-x2y1=0 [答案] A2.若向量a=(1,1),b=(-1,1),c=(4,2),则c=( )
A.3a+b B.3a-b
C.-a+3b D.a+3b
[答案] B
3.已知向量a=(1,2),b=(3,1),则b-a=( )
A.(-2,1) B.(2,-1)
C.(2,0) D.(4,3)
[答案] B
[解析] 本题考查向量的坐标运算.
b-a=(3,1)-(1,2)=(2,-1),选B.向量的减法是横坐标的差作为横坐标,纵坐标的差作为纵坐标. [答案] (-18,18),(-3,-3)[答案] (4,6)求向量的坐标或点的坐标 [规范解答] 如图,正三角形ABC的边长为2,则顶点A(0,0),B(2,0),C(2cos60°,2sin60°),[规律总结] (1)向量的坐标等于终点的坐标减去始点的相应坐标,只有当向量的始点在坐标原点时,向量的坐标才等于终点的坐标.
(2)求向量的坐标一般转化为求点的坐标,解题时常常结合几何图形,利用三角函数的定义和性质进行计算.如图所示,设向量a=(a1,a2),a的方向相对于x轴的旋转角为θ,由三角函数的定义可知a1=|a|cosθ,a2=|a|sinθ.用基底表示的坐标运算
[规律总结] 用基底a,b表示指定向量p时,可由平面向量基本定理设p=λa+μb,然后借助于坐标运算列方程(组)求解待定的系数.已知a=(10,-4),b=(3,1),c=(-2,3),试用b,c表示a.向量坐标表示下的共线问题
[规律总结] 求解直线或线段的交点问题,常规方法为写出直线或线段对应的直线方程,建立方程组求解,而利用向量方法借助共线向量可减少运算量,且思想简单明了.向量坐标的应用[规律总结] 向量的坐标运算为研究平面上问题带来方便,拓展了数形结合应用的空间,将几何问题向量化,并由向量运算的结果解释几何意义.
[规律总结] 两非零向量a,b共线,则它们的方向有相同或相反两种情况,求解时可能会漏掉一种情况而导致错误.
A.3a+b B.3a-b
C.-a+3b D.a+3b
[答案] B
3.已知向量a=(1,2),b=(3,1),则b-a=( )
A.(-2,1) B.(2,-1)
C.(2,0) D.(4,3)
[答案] B
[解析] 本题考查向量的坐标运算.
b-a=(3,1)-(1,2)=(2,-1),选B.向量的减法是横坐标的差作为横坐标,纵坐标的差作为纵坐标. [答案] (-18,18),(-3,-3)[答案] (4,6)求向量的坐标或点的坐标 [规范解答] 如图,正三角形ABC的边长为2,则顶点A(0,0),B(2,0),C(2cos60°,2sin60°),[规律总结] (1)向量的坐标等于终点的坐标减去始点的相应坐标,只有当向量的始点在坐标原点时,向量的坐标才等于终点的坐标.
(2)求向量的坐标一般转化为求点的坐标,解题时常常结合几何图形,利用三角函数的定义和性质进行计算.如图所示,设向量a=(a1,a2),a的方向相对于x轴的旋转角为θ,由三角函数的定义可知a1=|a|cosθ,a2=|a|sinθ.用基底表示的坐标运算
[规律总结] 用基底a,b表示指定向量p时,可由平面向量基本定理设p=λa+μb,然后借助于坐标运算列方程(组)求解待定的系数.已知a=(10,-4),b=(3,1),c=(-2,3),试用b,c表示a.向量坐标表示下的共线问题
[规律总结] 求解直线或线段的交点问题,常规方法为写出直线或线段对应的直线方程,建立方程组求解,而利用向量方法借助共线向量可减少运算量,且思想简单明了.向量坐标的应用[规律总结] 向量的坐标运算为研究平面上问题带来方便,拓展了数形结合应用的空间,将几何问题向量化,并由向量运算的结果解释几何意义.
[规律总结] 两非零向量a,b共线,则它们的方向有相同或相反两种情况,求解时可能会漏掉一种情况而导致错误.
