2.4.1-2.4.2 平面向量的坐标表示 课件4
文档属性
| 名称 | 2.4.1-2.4.2 平面向量的坐标表示 课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览




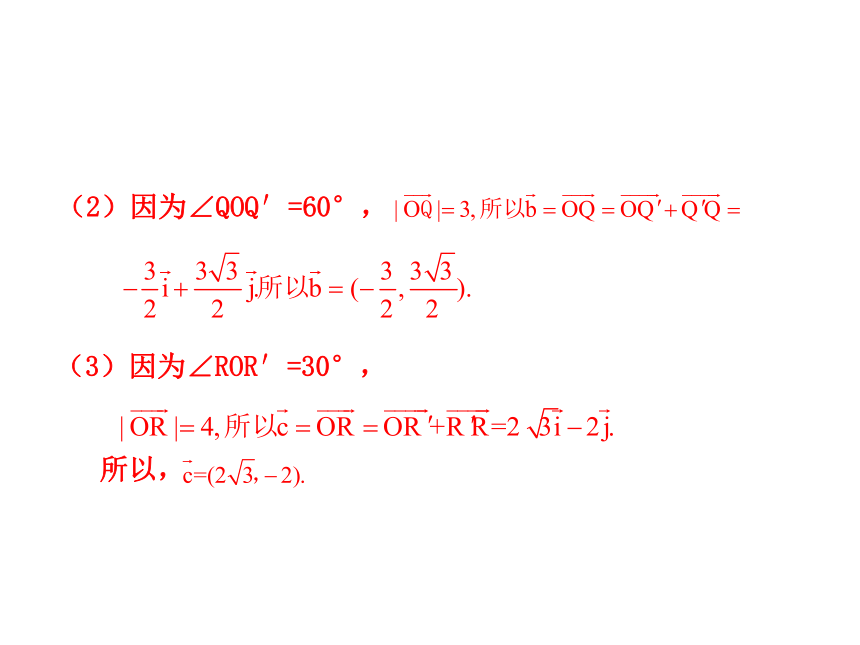
文档简介
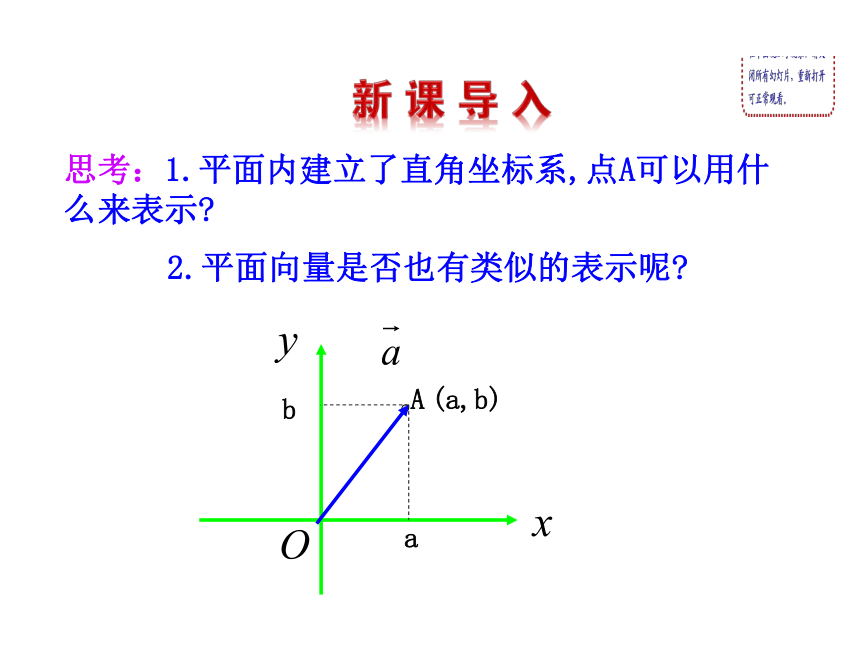
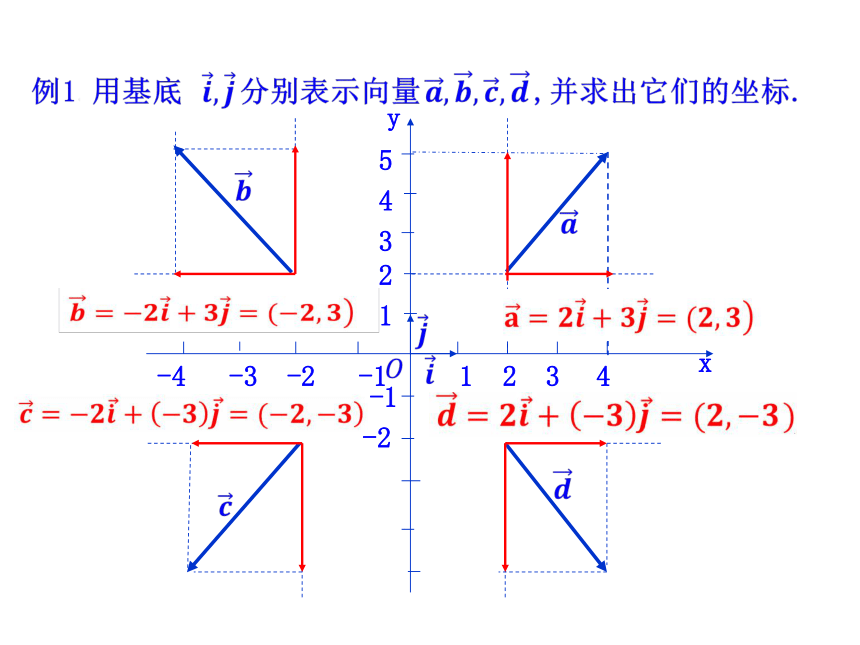
课件28张PPT。2.4.1-2.4.2 平面向量的坐标表示思考:1.平面内建立了直角坐标系,点A可以用什么来表示?2.平面向量是否也有类似的表示呢?A(a,b)ab1.掌握平面向量正交分解及其坐标表示.(重点)2.会用坐标表示平面向量的加、减及数乘运算.(重点)3.理解用坐标表示的平面向量共线的条件.(难点)xyo?①式是向量 的坐标表示.注意:每个向量都有唯一的坐标.探究点1 平面向量的坐标表示在直角坐标系内,我们分别??12-2-1xy453?????????-4 -3 -2 -1 1 2 3 4例2 在平面内以点O的正东方向为x轴正向,正北方向为y轴的正向建立直角坐标系,质点在平面内做直线运动,分别求下列位移向量的坐标(如图).解:设 并设P(x1,
y1),Q(x2,y2),R(x3,y3).
(1)由图可知,∠POP′=45°,
| |=2.
所以(2)因为∠QOQ′=60°,(3)因为∠ROR′=30°,
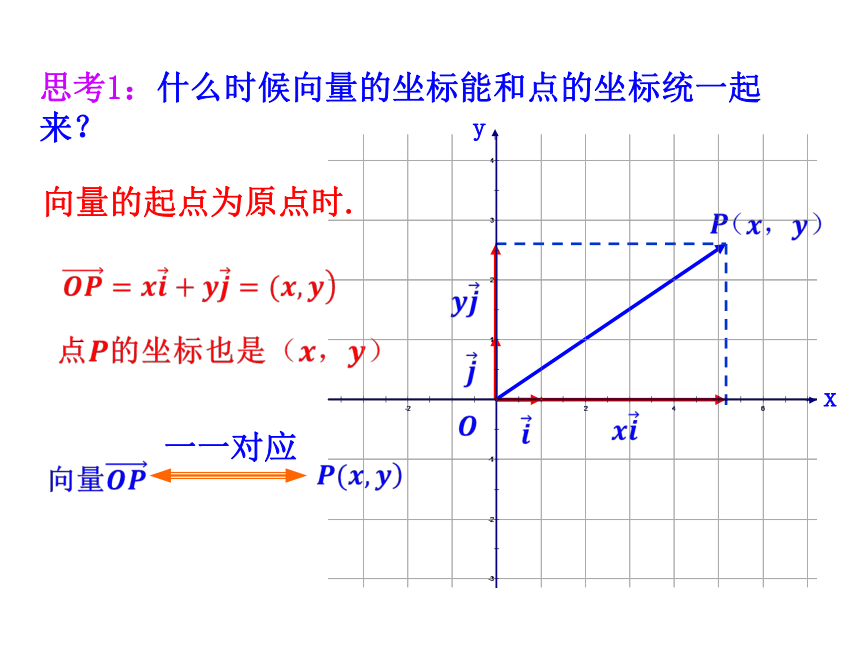
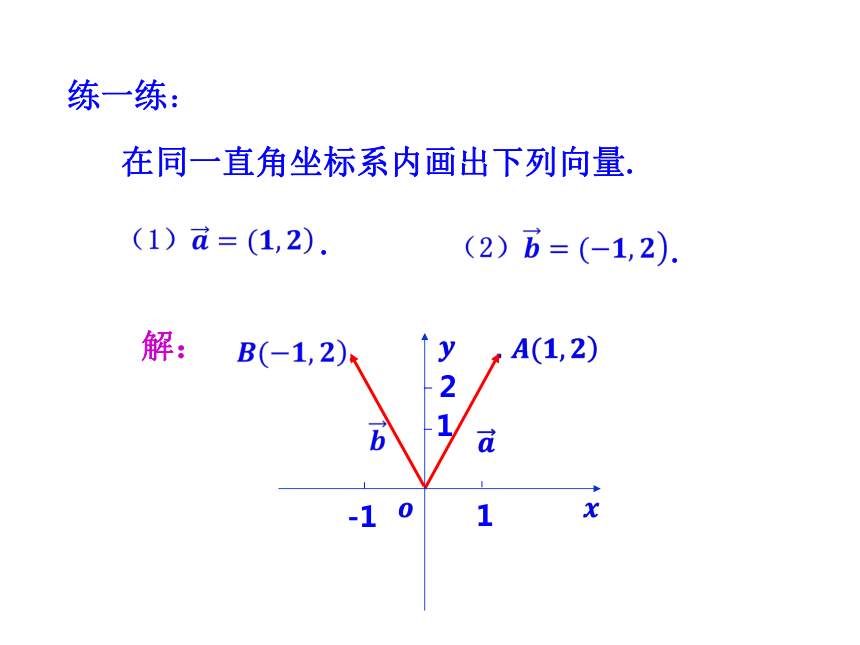
所以,?思考1:什么时候向量的坐标能和点的坐标统一起来?向量的起点为原点时.??????????一一对应yx在同一直角坐标系内画出下列向量.解:??练一练:..-1112思考2:相等向量的坐标有什么关系?提示:相等,与起点的位置无关.(1)任一平面向量都有唯一的坐标.(2)当向量的起点在原点时,向量终点的坐标即为向量的坐标.(3)相等的向量有相等的坐标.结论:思考3:全体有序实数对与坐标平面内的所有向量是否一一对应? 因此,在直角坐标系中,点或向量都可以看作有序实数对的直观形象.探究点2 平面向量线性运算的坐标表示解:结论1:向量和与差的坐标分别等于各向量相应坐标的和与差.结论2:实数与向量积的坐标分别等于实数与向量的相应坐标的乘积.A(x1,y1)OxyB(x2,y2)结论3:
一个向量的坐标等于其终点的相应坐标减去始点的相应坐标.向量坐标与向量始点、终点之间的关系因为解:得(0,2)-(1,0)=(-1,-2)-(x,y)即(-1,2)=(-1-x,-2-y),即点D的坐标为(0,-4).探究点3 向量平行(共线)的坐标表示我们可以得出:
定理:若两个向量(与坐标轴不平行)平行,则它们相应的坐标成比例.
定理:若两个向量相对应的坐标成比例,则它们平行.解:依题意,得1.若向量 =( )
A.(4,6) B.(-4,-6)
C.(-2,-2) D.(2,2)AB2.已知点A(-1,-5)和向量a=(2,3),若
则点B的坐标为( )
A(6,9) B(5,4) C(7,14) D(9,24)3.已知平面向量a=(2,4),b=(-1,1),
则2a-b等于 ( )
A.(5,7) B.(5,9) C.(3,7) D.(3,9)A4. 已知向量 , 若 , 则实数m等于( )
A. B.
C. 或 D.0C5.已知(1)若求x.(2)若求x.解:解得:1.向量的坐标的概念:2.对向量坐标表示的理解:3.平面向量的坐标运算.(1)任一平面向量都有唯一的坐标.(2)向量的坐标与其始点、终点坐标的关系.(3)相等的向量有相等的坐标.4.向量平行的坐标表示:不要对一切人都以不信任的眼光看待,但要谨慎而坚定.
——德谟克里特
y1),Q(x2,y2),R(x3,y3).
(1)由图可知,∠POP′=45°,
| |=2.
所以(2)因为∠QOQ′=60°,(3)因为∠ROR′=30°,
所以,?思考1:什么时候向量的坐标能和点的坐标统一起来?向量的起点为原点时.??????????一一对应yx在同一直角坐标系内画出下列向量.解:??练一练:..-1112思考2:相等向量的坐标有什么关系?提示:相等,与起点的位置无关.(1)任一平面向量都有唯一的坐标.(2)当向量的起点在原点时,向量终点的坐标即为向量的坐标.(3)相等的向量有相等的坐标.结论:思考3:全体有序实数对与坐标平面内的所有向量是否一一对应? 因此,在直角坐标系中,点或向量都可以看作有序实数对的直观形象.探究点2 平面向量线性运算的坐标表示解:结论1:向量和与差的坐标分别等于各向量相应坐标的和与差.结论2:实数与向量积的坐标分别等于实数与向量的相应坐标的乘积.A(x1,y1)OxyB(x2,y2)结论3:
一个向量的坐标等于其终点的相应坐标减去始点的相应坐标.向量坐标与向量始点、终点之间的关系因为解:得(0,2)-(1,0)=(-1,-2)-(x,y)即(-1,2)=(-1-x,-2-y),即点D的坐标为(0,-4).探究点3 向量平行(共线)的坐标表示我们可以得出:
定理:若两个向量(与坐标轴不平行)平行,则它们相应的坐标成比例.
定理:若两个向量相对应的坐标成比例,则它们平行.解:依题意,得1.若向量 =( )
A.(4,6) B.(-4,-6)
C.(-2,-2) D.(2,2)AB2.已知点A(-1,-5)和向量a=(2,3),若
则点B的坐标为( )
A(6,9) B(5,4) C(7,14) D(9,24)3.已知平面向量a=(2,4),b=(-1,1),
则2a-b等于 ( )
A.(5,7) B.(5,9) C.(3,7) D.(3,9)A4. 已知向量 , 若 , 则实数m等于( )
A. B.
C. 或 D.0C5.已知(1)若求x.(2)若求x.解:解得:1.向量的坐标的概念:2.对向量坐标表示的理解:3.平面向量的坐标运算.(1)任一平面向量都有唯一的坐标.(2)向量的坐标与其始点、终点坐标的关系.(3)相等的向量有相等的坐标.4.向量平行的坐标表示:不要对一切人都以不信任的眼光看待,但要谨慎而坚定.
——德谟克里特
