2.5 从力做的功到向量的数量积 课件1
文档属性
| 名称 | 2.5 从力做的功到向量的数量积 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 413.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览






文档简介
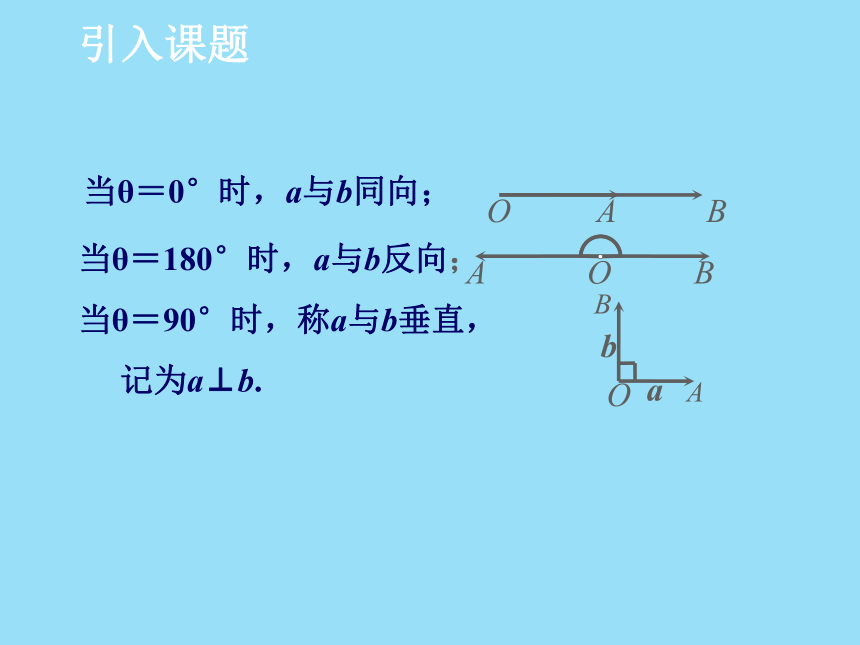
课件17张PPT。2.5 从力做的功到向量的数量积第二章 平面向量引入课题已知两个非零向量 a 和b ,作 ,则∠AOB=θ (0°≤θ ≤180°)叫做向量 a 与b 的夹角。OBθ引入课题知识点1:向量“数量积”的概念一个物体在力F的作用下产生位移S(如图)θFS那么力F所做的功W为:W=|F| |S|cosθ 其中θ是F与S的夹角.从力所做的功出发,我们引入向量“数量积”的概念。典型例题典型例题(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
=a2-b2.想一想当a · b<0时, cos?<0,为钝角三角形当a · b=0时,为直角三角形探究点2 投影的概念 向量数量积的
几何意义数量积 a · b 等于a 的模| a |与 b 在 a 的方向上的投影| b |cos ?的乘积.探究点2 投影的概念 投影的作图:| b |cos ??0| b |cos ???b?B1B1B探究点3 数量积的定义 已知两个非零向量a和b ,它们的夹角为? ,我们把数量 叫做a 与b 的数量积(或内积),记作a · b ,即(1)两向量的数量积是一个数量,注意探究点4 运算率 设a,b为任意向量,λ,μ为任意实数,则有:
① λ(μa)=(λμ) a
② (λ+μ) a=λa+μa
③ λ(a+b)=λa+λb课堂练习课堂练习证明: (a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.课堂练习回顾实数运算中有关的运算律,类比数量积得运算律:在实数中 在向量运算中
交换律: ab=ba ( )
结合律: (ab)c=a(bc) ( )
( )
分配律: (a+b)c=ab+bc ( )
消去律: ab=bc(b≠0) a=c ( )√√√ × ×典型例题..×√..×不为课堂小结1.向量的数量积运算类似于多项式运算
2.数量积a?b等于a的长度 与b在a的方向上的投影
=a·a+b·a-a·b-b·b
=a2-b2.想一想当a · b<0时, cos?<0,为钝角三角形当a · b=0时,为直角三角形探究点2 投影的概念 向量数量积的
几何意义数量积 a · b 等于a 的模| a |与 b 在 a 的方向上的投影| b |cos ?的乘积.探究点2 投影的概念 投影的作图:| b |cos ??0| b |cos ???b?B1B1B探究点3 数量积的定义 已知两个非零向量a和b ,它们的夹角为? ,我们把数量 叫做a 与b 的数量积(或内积),记作a · b ,即(1)两向量的数量积是一个数量,注意探究点4 运算率 设a,b为任意向量,λ,μ为任意实数,则有:
① λ(μa)=(λμ) a
② (λ+μ) a=λa+μa
③ λ(a+b)=λa+λb课堂练习课堂练习证明: (a+b)2=(a+b)·(a+b)=(a+b)·a+(a+b)·b=a·a+b·a+a·b+b·b=a2+2a·b+b2.课堂练习回顾实数运算中有关的运算律,类比数量积得运算律:在实数中 在向量运算中
交换律: ab=ba ( )
结合律: (ab)c=a(bc) ( )
( )
分配律: (a+b)c=ab+bc ( )
消去律: ab=bc(b≠0) a=c ( )√√√ × ×典型例题..×√..×不为课堂小结1.向量的数量积运算类似于多项式运算
2.数量积a?b等于a的长度 与b在a的方向上的投影
