2.5 从力做的功到向量的数量积 课件4
文档属性
| 名称 | 2.5 从力做的功到向量的数量积 课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 930.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览







文档简介
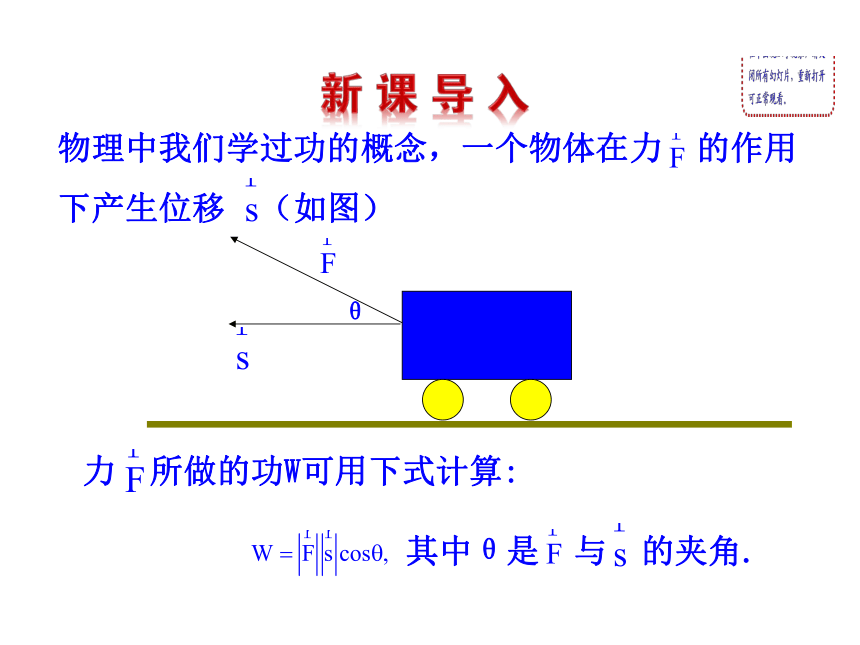
课件30张PPT。2.5 从力做的功到向量的数量积物理中我们学过功的概念,一个物体在力 的作用
下产生位移 (如图)θ力 所做的功W可用下式计算:
其中θ是 与 的夹角.当0°≤θ<90°时,W>0, 即力F做正功;
当θ=90°时,W=0,即力F不做功;
当90°<θ≤180°时,W<0,即力F做负功.从力所做的功出发,我们引入向量的数量积的概念.1.通过物理中“功”等实例,理解平面向量数量积的含义及其物理意义、几何意义.(重点)
2.体会平面向量的数量积与向量射影的关系.3.掌握平面向量数量积的重要性质及运算律和它的一些简单应用.(重点)
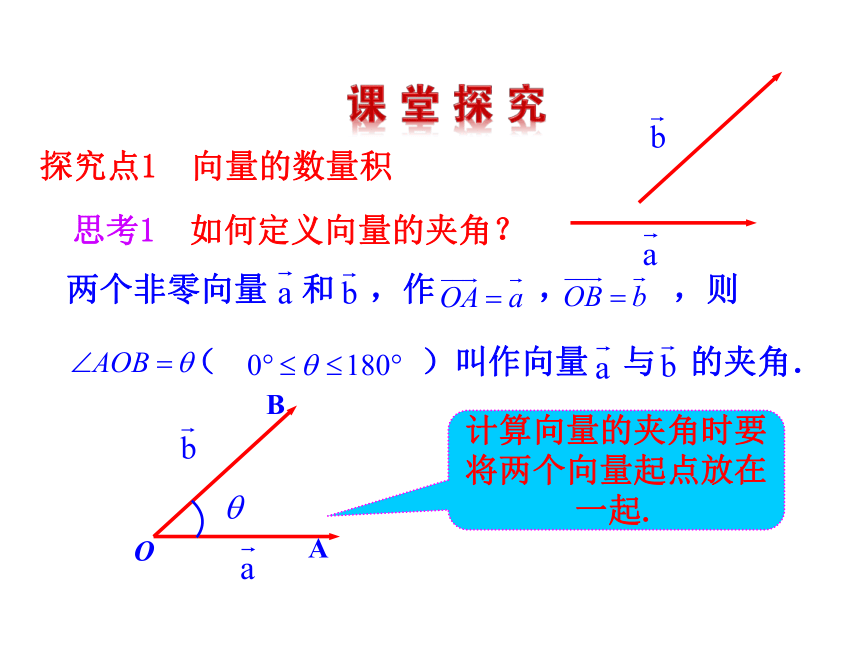
4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.(难点)两个非零向量 和 ,作 , ,则
( )叫作向量 与 的夹角.思考1 如何定义向量的夹角?计算向量的夹角时要将两个向量起点放在一起.探究点1 向量的数量积由于零向量的方向是任意的,为方便起见,
规定:零向量可与任一向量垂直. ,过点B 作BB1垂直于直线OA,垂足为
B1,则| | cosθ叫作向量 在 方向
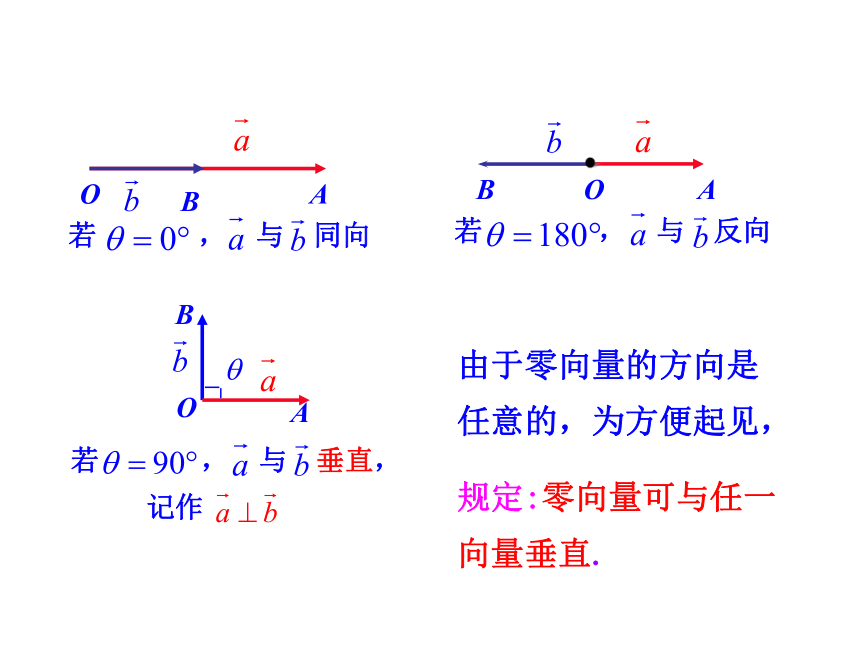
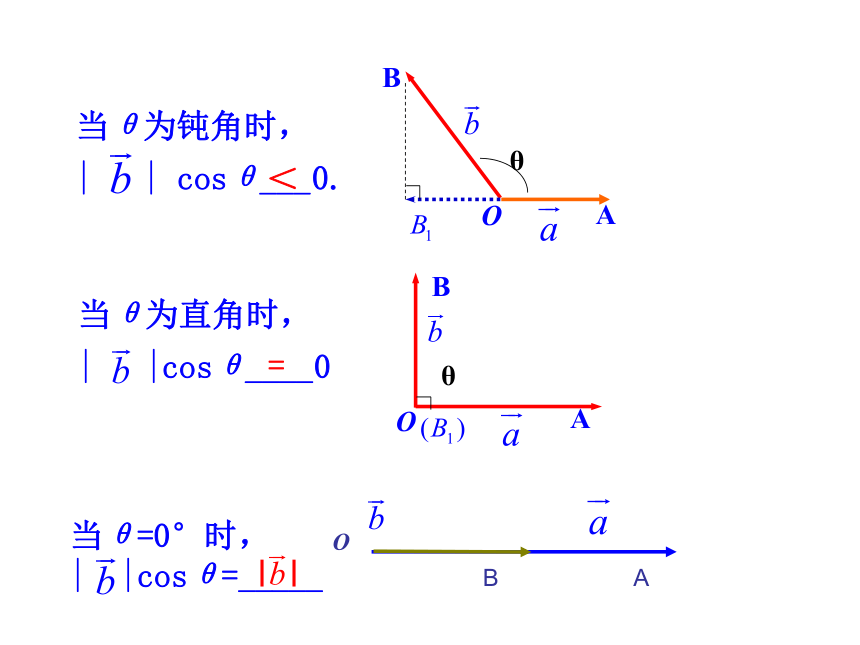
上的射影(也叫投影).当θ为锐角时,
| | cosθ_____0>思考2 什么是向量的射影?B1OBA当θ=0°时,
| |cosθ=_____| |当θ为钝角时,
| | cosθ___0.当θ为直角时,
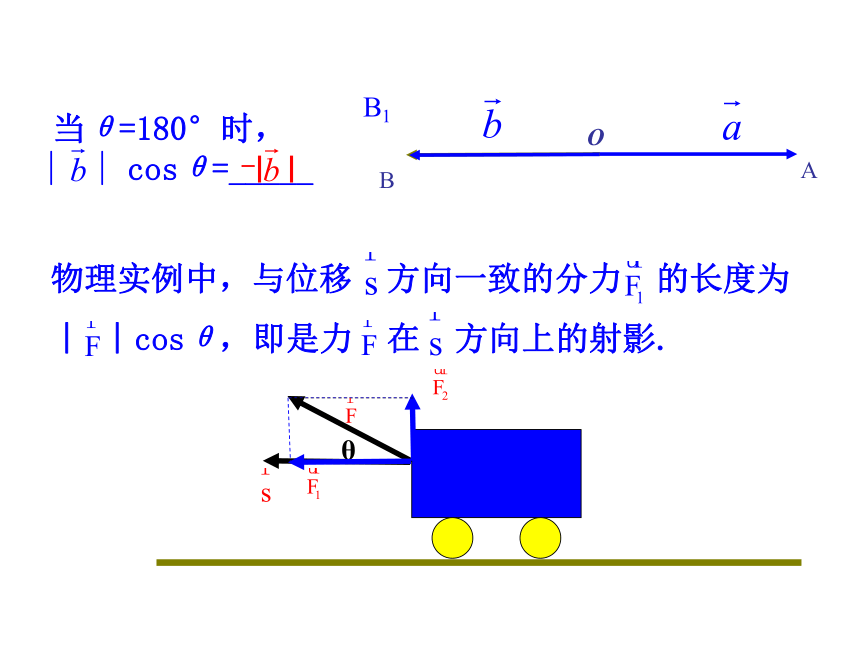
| |cosθ____0<=OBA当θ=180°时,
| | cosθ=_____B1物理实例中,与位移 方向一致的分力 的长度为
︱ ︱cosθ,即是力 在 方向上的射影.θ-| |思考3 平面向量的数量积的定义如何?
已知两个向量 与 ,它们的夹角为θ,我们把
| || |cosθ叫作 与 的数量积(或内积).记作 ·
· =| || | cosθ注意:向量的数量积是一个数量.特别地:零向量与任一向量 的数量积为0.⑵ 已知 =(1,1), =(2,0), 与 的夹角θ= 45°.
求 · .例1 ⑴ 已知| |=3,| |=4,且 与 的夹角θ=150°,求 · .解: · =| || |cosθ=3×4×cos150°
=3×4×(- )=-6解: | | = , | |=2, θ=45°,
所以 · =| || |cosθ= ×2×cos45°= 2.思考4 数量积的几何意义是什么?特别提醒:
1.
2.若 是单位向量,则重要性质:
1.若 是单位向量,则:
2.
3.
4.
5.
当且仅当 ∥ 时等号成立. 思考5 数量积的物理意义是什么?反之成立吗?解答:不成立.解答:成立.思考:探究点2 向量的数量积的运算律练习:判断下列说法的正误√×××××√3.若 ≠ , · =0,则 = 2.若 ≠ ,则对任一非零向量 ,有 · ≠0.1.若 = ,则对任一向量 ,有 · = 0 .4.若 · =0,则 , 中至少有一个为 .5.若 ≠ , · = · ,则 = 6.若 · = · ,且 ≠ ,当且仅当 = 时成立.7.对任意向量 有例2 在ΔABC中,设边BC,CA,AB的长度分别为a,b,c,证明:
a2=b2+c2–2 bccosA,
b2=c2+a2–2cacosB,
c2=a2+b2–2abcosC.证明:设 则同理可证其他两式,我们把这个结果称为余弦定理.=b2+c2–2 bccosA......向量法证明几何问题的步骤:
1.将三角形的边用有向线段表示.
2.根据向量的运算及向量的几何意义,写出向量之间的关系.
3.通过平方和向量的数量积整理出所要的结果.例3 证明菱形的两条对角线互相垂直.证明:菱形ABCD中,AB=AD,由于可得=0,
所以,即菱形的两条对角线互相垂直.ABCDO..证明线段垂直的方法:
1.取两个不共线的向量作基底.
2.将要证明的向量用这两个向量表示.
3.利用 进行证明.【提升总结】例4 已知单位向量 , 的夹角为60°,求向量
, 的夹角.解:由单位向量 , 的夹角为60°,得又设 与 的夹角为 , 由①②可得又 所以 .
即向量 与 的夹角为 .技巧点拨:
1.以 , 为基底,计算 的值.
2.利用向量的夹角公式计算. 1.判断下列说法的正误:
(1)平面向量的数量积可以比较大小. ( )
(2) ( )
(3)已知 为非零向量,因为0× = , · = 0,
所以 = ( )
(4) ( )√×××2.△ABC中, 则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
【解析】由 知∠ABC为锐角;
由 知,∠ACB为钝角.C3.在△ABC中,M是线段BC的中点,AM=3,BC=10,
则_______.-16 -24.若|a|=1,|b|=2,且a,b反向,则a·b=_______.解:本节课主要学习了:
1.向量的夹角.
2.向量的射影.
3.向量的数量积.
4.向量的数量积的几何意义和物理意义.
5.向量的数量积的性质和运算律.不会宽容别人的人,是不配受到别人的宽容的.
——贝尔奈
下产生位移 (如图)θ力 所做的功W可用下式计算:
其中θ是 与 的夹角.当0°≤θ<90°时,W>0, 即力F做正功;
当θ=90°时,W=0,即力F不做功;
当90°<θ≤180°时,W<0,即力F做负功.从力所做的功出发,我们引入向量的数量积的概念.1.通过物理中“功”等实例,理解平面向量数量积的含义及其物理意义、几何意义.(重点)
2.体会平面向量的数量积与向量射影的关系.3.掌握平面向量数量积的重要性质及运算律和它的一些简单应用.(重点)
4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.(难点)两个非零向量 和 ,作 , ,则
( )叫作向量 与 的夹角.思考1 如何定义向量的夹角?计算向量的夹角时要将两个向量起点放在一起.探究点1 向量的数量积由于零向量的方向是任意的,为方便起见,
规定:零向量可与任一向量垂直. ,过点B 作BB1垂直于直线OA,垂足为
B1,则| | cosθ叫作向量 在 方向
上的射影(也叫投影).当θ为锐角时,
| | cosθ_____0>思考2 什么是向量的射影?B1OBA当θ=0°时,
| |cosθ=_____| |当θ为钝角时,
| | cosθ___0.当θ为直角时,
| |cosθ____0<=OBA当θ=180°时,
| | cosθ=_____B1物理实例中,与位移 方向一致的分力 的长度为
︱ ︱cosθ,即是力 在 方向上的射影.θ-| |思考3 平面向量的数量积的定义如何?
已知两个向量 与 ,它们的夹角为θ,我们把
| || |cosθ叫作 与 的数量积(或内积).记作 ·
· =| || | cosθ注意:向量的数量积是一个数量.特别地:零向量与任一向量 的数量积为0.⑵ 已知 =(1,1), =(2,0), 与 的夹角θ= 45°.
求 · .例1 ⑴ 已知| |=3,| |=4,且 与 的夹角θ=150°,求 · .解: · =| || |cosθ=3×4×cos150°
=3×4×(- )=-6解: | | = , | |=2, θ=45°,
所以 · =| || |cosθ= ×2×cos45°= 2.思考4 数量积的几何意义是什么?特别提醒:
1.
2.若 是单位向量,则重要性质:
1.若 是单位向量,则:
2.
3.
4.
5.
当且仅当 ∥ 时等号成立. 思考5 数量积的物理意义是什么?反之成立吗?解答:不成立.解答:成立.思考:探究点2 向量的数量积的运算律练习:判断下列说法的正误√×××××√3.若 ≠ , · =0,则 = 2.若 ≠ ,则对任一非零向量 ,有 · ≠0.1.若 = ,则对任一向量 ,有 · = 0 .4.若 · =0,则 , 中至少有一个为 .5.若 ≠ , · = · ,则 = 6.若 · = · ,且 ≠ ,当且仅当 = 时成立.7.对任意向量 有例2 在ΔABC中,设边BC,CA,AB的长度分别为a,b,c,证明:
a2=b2+c2–2 bccosA,
b2=c2+a2–2cacosB,
c2=a2+b2–2abcosC.证明:设 则同理可证其他两式,我们把这个结果称为余弦定理.=b2+c2–2 bccosA......向量法证明几何问题的步骤:
1.将三角形的边用有向线段表示.
2.根据向量的运算及向量的几何意义,写出向量之间的关系.
3.通过平方和向量的数量积整理出所要的结果.例3 证明菱形的两条对角线互相垂直.证明:菱形ABCD中,AB=AD,由于可得=0,
所以,即菱形的两条对角线互相垂直.ABCDO..证明线段垂直的方法:
1.取两个不共线的向量作基底.
2.将要证明的向量用这两个向量表示.
3.利用 进行证明.【提升总结】例4 已知单位向量 , 的夹角为60°,求向量
, 的夹角.解:由单位向量 , 的夹角为60°,得又设 与 的夹角为 , 由①②可得又 所以 .
即向量 与 的夹角为 .技巧点拨:
1.以 , 为基底,计算 的值.
2.利用向量的夹角公式计算. 1.判断下列说法的正误:
(1)平面向量的数量积可以比较大小. ( )
(2) ( )
(3)已知 为非零向量,因为0× = , · = 0,
所以 = ( )
(4) ( )√×××2.△ABC中, 则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
【解析】由 知∠ABC为锐角;
由 知,∠ACB为钝角.C3.在△ABC中,M是线段BC的中点,AM=3,BC=10,
则_______.-16 -24.若|a|=1,|b|=2,且a,b反向,则a·b=_______.解:本节课主要学习了:
1.向量的夹角.
2.向量的射影.
3.向量的数量积.
4.向量的数量积的几何意义和物理意义.
5.向量的数量积的性质和运算律.不会宽容别人的人,是不配受到别人的宽容的.
——贝尔奈
