2.6 平面向量数量积的坐标表示 课件1
文档属性
| 名称 | 2.6 平面向量数量积的坐标表示 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 659.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览








文档简介
课件27张PPT。2.6 平面向量数量积的坐标表示 如果没有运算,向量只是一个“路标”,因为有了运算,向量的力量无限.
下面就让平面向量数量积坐标表示的运算顺利起航吧!1.掌握“平面向量的数量积的坐标表示”这个重要的知识点.(重点)
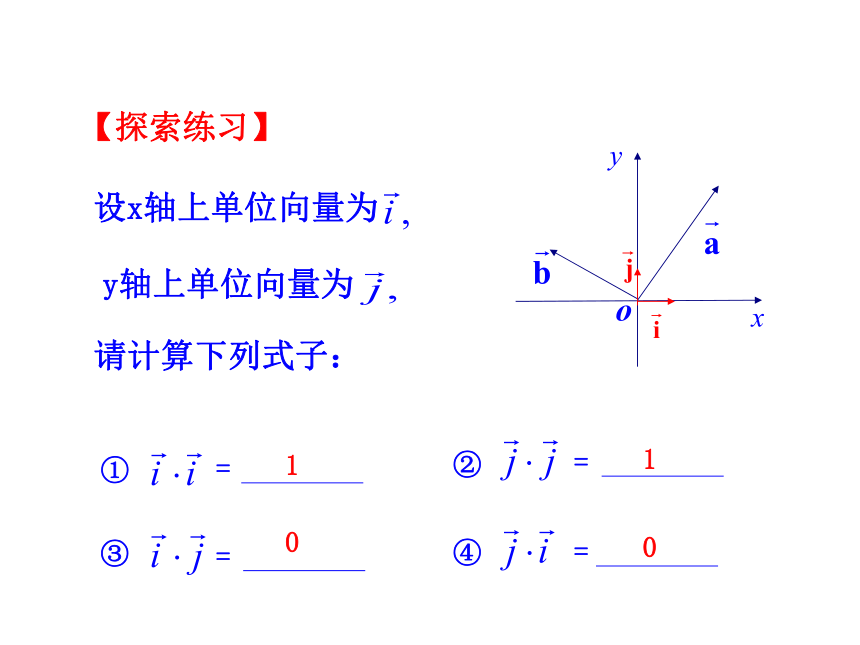
2.会用“平面向量的数量积的坐标表示”的有关知识解决实际问题.如判断垂直、求模、夹角等.(难点)思考1:向量的加法、减法、数乘都可以用“坐标语言”表示,向量的数量积能否由“坐标语言”来表示? 若两个向量请计算下列式子:设x轴上单位向量为y轴上单位向量为1100【探索练习】这就是说,两个向量的数量积等于相应坐标乘积的和,即所以练一练:求值区分好横纵坐标,准确代入数值,精心计算.
思考2:如何用向量的坐标来表示两向量数量积的相关性质?坐标表示为:(1)垂直的充要条件:.(2)求模公式:坐标表示为:特别地:坐标表示为:(3)夹角公式:例1 已知 , ,求向量 与 的夹角的余弦值. 技巧方法:
1.细心代入,精确计算.
2.分步计算,化整为零.例2 求以点C(ɑ,b)为圆心,r为半径的圆的方程.特别地:如果圆心在坐标原点上,这时a=0,b=0 ,那么圆的标准方程为 x2+y2=r2.xoyCM提升总结:
设圆上任意一点M(x,y),构造向量 ,利用向量的模为定值,列出相等关系,化简即得所求曲线的方程.yxo.例3 已知圆C:(x-ɑ)2+(y-b)2=r2,求与
圆C相切于点Po(xo,yo)的切线方程.(如图)CP0P.若ɑ=0,b=0,圆的标准方程为x2+y2=r2,与它相切于
P0(x0,y0)的切线方程为x0(x-x0)+y0(y-y0)=0,
由于x02+y02=r2,故此方程可化为x0x+y0y=r2.特别地:提升总结:
将相关向量用坐标表示,根据互相垂直的向量的数量积等于零,写出表达式.直线的方向向量 由解析几何知,给定斜率为k的直线l,则向量
=(1,k)与直线l共线,我们把与直线l共线的非
零向量 称为直线l的方向向量.例4 已知直线l1:3x+4y-12=0和l2:7x+y-28=0,求直线l1和l2的夹角.解: 任取直线l1和l2的方向向量提升总结:
利用斜率为k的直线l的方向向量为 =(1,k),写出直线l1和l2的方向向量,然后运用向量的夹角公式计算出夹角的余弦值,从而求出夹角.
注意:直线的夹角取值范围[0, ],当求出的向量的夹角为钝角时,应取其补角.1.已知A(1,2),B(4,0),C(8,6),D(5,8),则四边
形ABCD的形状是 .3.给定两个向量 若 ⊥∥ 若矩形2.已知点A(-1,1),B(1,2),C(-2,-1),
D(3,4),则向量 在 方向上的投影为( )
A. B. C.- D.- A4.已知单位向量35.已知向量 ,则 的最大值为____. 6.已知向量
(1)求 与 的夹角θ的余弦值.
(2)若向量 与 垂直,求λ的值.理解和应用向量坐标表示的公式解决问题:1.数量积的坐标表示2.向量坐标表示的求模公式3.平面内两点间的距离公式4.两向量夹角的余弦5.向量垂直的判定不患位之不尊,而患德之不崇;不耻禄之不伙,而耻智之不博.
——张衡
下面就让平面向量数量积坐标表示的运算顺利起航吧!1.掌握“平面向量的数量积的坐标表示”这个重要的知识点.(重点)
2.会用“平面向量的数量积的坐标表示”的有关知识解决实际问题.如判断垂直、求模、夹角等.(难点)思考1:向量的加法、减法、数乘都可以用“坐标语言”表示,向量的数量积能否由“坐标语言”来表示? 若两个向量请计算下列式子:设x轴上单位向量为y轴上单位向量为1100【探索练习】这就是说,两个向量的数量积等于相应坐标乘积的和,即所以练一练:求值区分好横纵坐标,准确代入数值,精心计算.
思考2:如何用向量的坐标来表示两向量数量积的相关性质?坐标表示为:(1)垂直的充要条件:.(2)求模公式:坐标表示为:特别地:坐标表示为:(3)夹角公式:例1 已知 , ,求向量 与 的夹角的余弦值. 技巧方法:
1.细心代入,精确计算.
2.分步计算,化整为零.例2 求以点C(ɑ,b)为圆心,r为半径的圆的方程.特别地:如果圆心在坐标原点上,这时a=0,b=0 ,那么圆的标准方程为 x2+y2=r2.xoyCM提升总结:
设圆上任意一点M(x,y),构造向量 ,利用向量的模为定值,列出相等关系,化简即得所求曲线的方程.yxo.例3 已知圆C:(x-ɑ)2+(y-b)2=r2,求与
圆C相切于点Po(xo,yo)的切线方程.(如图)CP0P.若ɑ=0,b=0,圆的标准方程为x2+y2=r2,与它相切于
P0(x0,y0)的切线方程为x0(x-x0)+y0(y-y0)=0,
由于x02+y02=r2,故此方程可化为x0x+y0y=r2.特别地:提升总结:
将相关向量用坐标表示,根据互相垂直的向量的数量积等于零,写出表达式.直线的方向向量 由解析几何知,给定斜率为k的直线l,则向量
=(1,k)与直线l共线,我们把与直线l共线的非
零向量 称为直线l的方向向量.例4 已知直线l1:3x+4y-12=0和l2:7x+y-28=0,求直线l1和l2的夹角.解: 任取直线l1和l2的方向向量提升总结:
利用斜率为k的直线l的方向向量为 =(1,k),写出直线l1和l2的方向向量,然后运用向量的夹角公式计算出夹角的余弦值,从而求出夹角.
注意:直线的夹角取值范围[0, ],当求出的向量的夹角为钝角时,应取其补角.1.已知A(1,2),B(4,0),C(8,6),D(5,8),则四边
形ABCD的形状是 .3.给定两个向量 若 ⊥∥ 若矩形2.已知点A(-1,1),B(1,2),C(-2,-1),
D(3,4),则向量 在 方向上的投影为( )
A. B. C.- D.- A4.已知单位向量35.已知向量 ,则 的最大值为____. 6.已知向量
(1)求 与 的夹角θ的余弦值.
(2)若向量 与 垂直,求λ的值.理解和应用向量坐标表示的公式解决问题:1.数量积的坐标表示2.向量坐标表示的求模公式3.平面内两点间的距离公式4.两向量夹角的余弦5.向量垂直的判定不患位之不尊,而患德之不崇;不耻禄之不伙,而耻智之不博.
——张衡
