2.7.2 向量的应用举例 课件2
图片预览









文档简介
课件34张PPT。2.7.2 向量的应用举例 平行、垂直、夹角、距离、全等、相似等,是平面几何中常见的问题,而这些问题都可以由向量的线性运算及数量积表示出来.因此,平面几何中的某些问题可以用向量方法来解决,但解决问题的数学思想、方法和技能,需要我们在实践中去探究、领会和总结.1.了解直线法向量的概念.
2.掌握利用向量方法解决平面几何问题,体会解析法和向量方法的区别与联系.(重点)
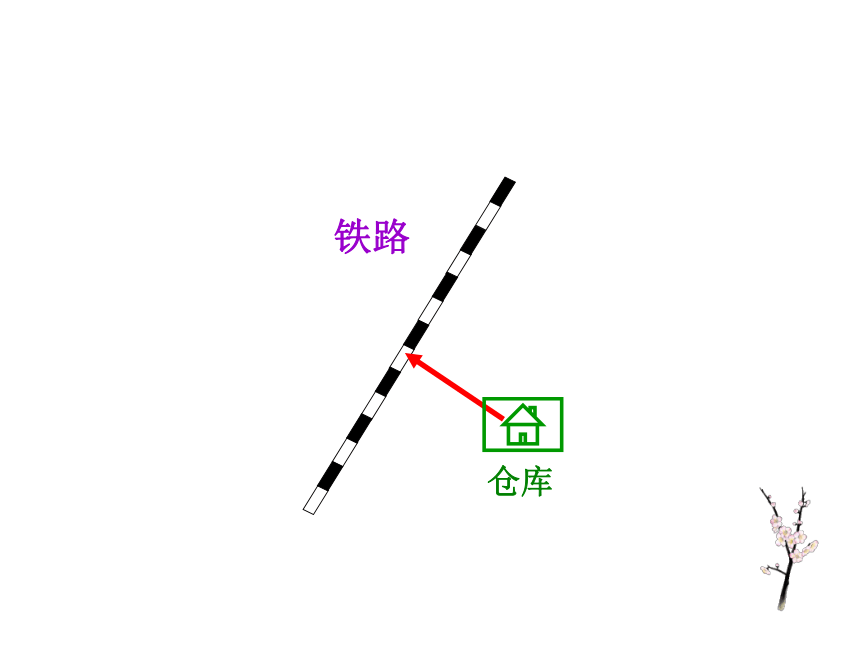
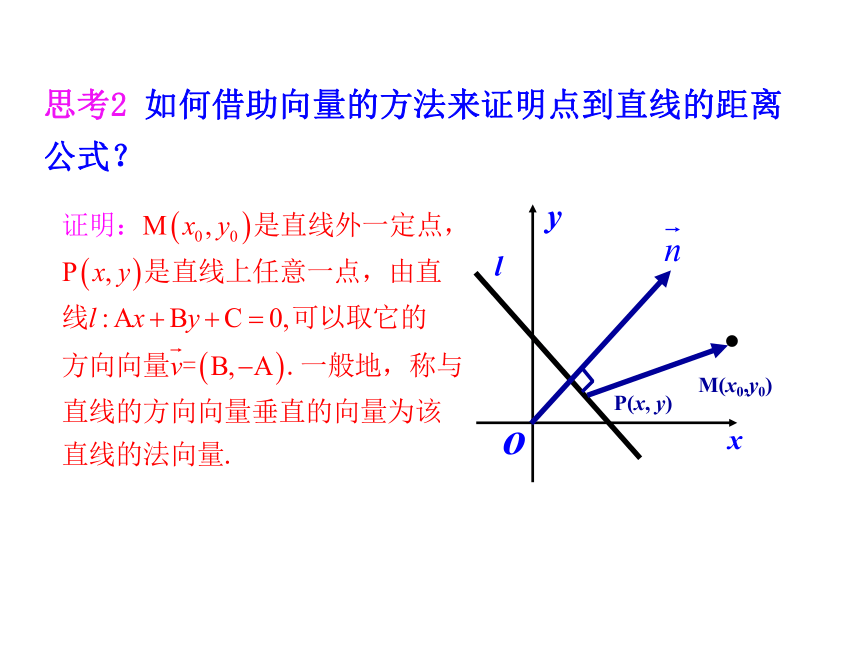
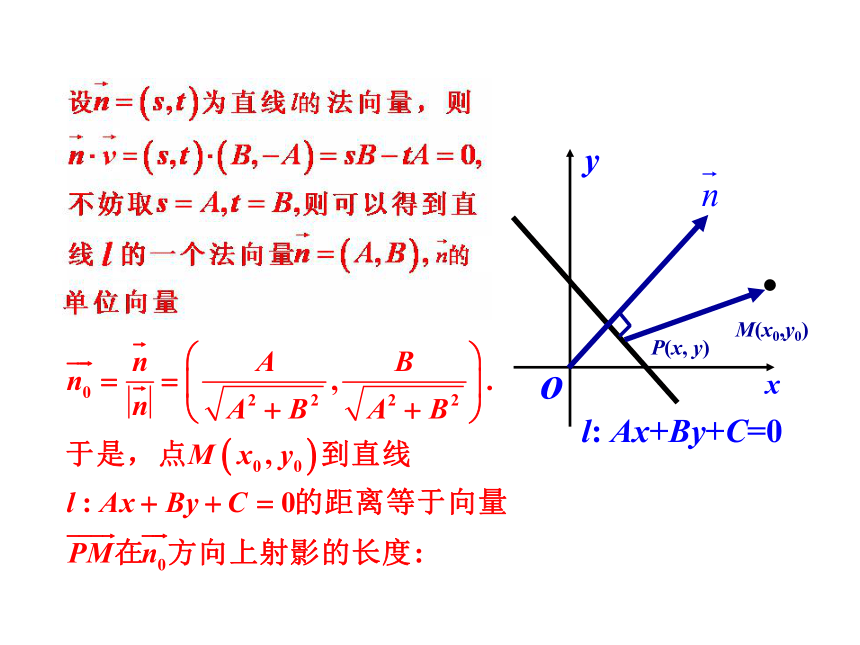
3.会用向量方法解决物理问题,会用所学知识解决实际问题.(难点)思考1 用向量方法解决平面几何问题的基本思路是什么?几何问题向量化 向量运算关系化 向量关系几何化.探究点1 点到直线的距离公式仓库铁路点到直线的距离llM.: Ax+By+C=0(x0,y0)点到直线的距离已知点M(x0, y0)和直线l:Ax+By+C=0.则点M到直线 l 的距离d为:点到直线的距离公式思考2 如何借助向量的方法来证明点到直线的距离公式?ll: Ax+By+C=01.在使用该公式前,需将直线方程化为一般式.
2. A=0或B=0,此公式也成立,但当A=0且B=0时一般不用此公式计算距离.特别提醒:当A=0或B=0时,直线方程为y=y1或x=x1的形式.QQ(x0,y1)(x1,y0)技巧方法:
认清公式的形式,找准每一个变量代表的数值,准确代入,精确计算.求下列各点到相应直线的距离课堂练习探究点2 几何中的应用举例
例2 如图,已知AD,BE,CF分别是△ABC的三条高,
求证:AD,BE,CF相交于同一点.思路分析 解决此类问题一般是将相关的线段用向量表示,利用向量的三角形法则和平行四边形法则,结合题目中的已知条件进行运算,得出结果,再翻译成几何语言 .简述:1.建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
2.通过向量运算,研究几何元素之间的关系,如距离、夹角等问题.
3.把运算结果“翻译”成几何元素.思考3 根据例题你能总结一下利用向量法解决平面几何问题的基本思路吗?用向量方法解决平面几何问题的“三步曲”:形到向量向量的运算向量和数到形思考4 物理中力的合成与分解中体现了向量的哪种运算?
提示:体现了向量的加减法的运算.
思考5 在物体的运动过程中,是否力越大,做的功就越多?
提示:不一定.力所做的功不仅取决于力的大小,还和力与物体运动方向的夹角有关系.探究点3 物理中的应用举例例3 一架飞机从A地向北偏西60°的方向飞行
1 000km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°,并且A,C两地相距2 000km,求飞机从B地到C地的位移.分析: 要求飞机从B地到C地的位移,需要解决两个问题:
⑴利用解三角形的知识求线段BC的长度.
⑵求BC与基线的夹角.向量解决航空、航海问题方法:
1.按照题意正确作图.
2.分析图形的边角关系.
3.利用平面几何的知识求出答案. 30°分析:本题是向量在物理学中“力学问题”上应用的例子,可以清楚地看出向量的直接作用,根据向量数量积的几何意义,可知对物体所做的功即是表示力的向量和表示位移的向量的数量积.例4 已知力 与水平方向的夹角为30°(斜向上),
大小为50 N,一个质量为8 kg的木块受力 的作用在
动摩擦因数μ=0.02的水平平面上运动了20 m.问力
和摩擦力 所做的功分别为多少?(g=10 m/s2)向量解决物理问题方法:
1.将物理中的矢量用向量表示.
2.找出向量与向量的夹角.
3.利用向量的数量积计算功.1.证明直径所对的圆周角是直角.如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点,不与AB重合.求证
∠ACB=90°.证明:设 则 ,
由此可得:即 , ∠ACB=90°.思路分析本题方法:
1.计算速度的合速度.
2.计算时间必须使速度的方向和位移的方向一致.答:行驶航程最短时,所用的时间是3.1 min.注意:用该公式时应先将直线方程化为一般式. 1.点到直线的距离公式: ,2.掌握用向量方法解决平面几何问题的三个步骤:不奋苦而求速效,只落得少日浮夸,老来窘隘而已.
——郑板桥
2.掌握利用向量方法解决平面几何问题,体会解析法和向量方法的区别与联系.(重点)
3.会用向量方法解决物理问题,会用所学知识解决实际问题.(难点)思考1 用向量方法解决平面几何问题的基本思路是什么?几何问题向量化 向量运算关系化 向量关系几何化.探究点1 点到直线的距离公式仓库铁路点到直线的距离llM.: Ax+By+C=0(x0,y0)点到直线的距离已知点M(x0, y0)和直线l:Ax+By+C=0.则点M到直线 l 的距离d为:点到直线的距离公式思考2 如何借助向量的方法来证明点到直线的距离公式?ll: Ax+By+C=01.在使用该公式前,需将直线方程化为一般式.
2. A=0或B=0,此公式也成立,但当A=0且B=0时一般不用此公式计算距离.特别提醒:当A=0或B=0时,直线方程为y=y1或x=x1的形式.QQ(x0,y1)(x1,y0)技巧方法:
认清公式的形式,找准每一个变量代表的数值,准确代入,精确计算.求下列各点到相应直线的距离课堂练习探究点2 几何中的应用举例
例2 如图,已知AD,BE,CF分别是△ABC的三条高,
求证:AD,BE,CF相交于同一点.思路分析 解决此类问题一般是将相关的线段用向量表示,利用向量的三角形法则和平行四边形法则,结合题目中的已知条件进行运算,得出结果,再翻译成几何语言 .简述:1.建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题.
2.通过向量运算,研究几何元素之间的关系,如距离、夹角等问题.
3.把运算结果“翻译”成几何元素.思考3 根据例题你能总结一下利用向量法解决平面几何问题的基本思路吗?用向量方法解决平面几何问题的“三步曲”:形到向量向量的运算向量和数到形思考4 物理中力的合成与分解中体现了向量的哪种运算?
提示:体现了向量的加减法的运算.
思考5 在物体的运动过程中,是否力越大,做的功就越多?
提示:不一定.力所做的功不仅取决于力的大小,还和力与物体运动方向的夹角有关系.探究点3 物理中的应用举例例3 一架飞机从A地向北偏西60°的方向飞行
1 000km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°,并且A,C两地相距2 000km,求飞机从B地到C地的位移.分析: 要求飞机从B地到C地的位移,需要解决两个问题:
⑴利用解三角形的知识求线段BC的长度.
⑵求BC与基线的夹角.向量解决航空、航海问题方法:
1.按照题意正确作图.
2.分析图形的边角关系.
3.利用平面几何的知识求出答案. 30°分析:本题是向量在物理学中“力学问题”上应用的例子,可以清楚地看出向量的直接作用,根据向量数量积的几何意义,可知对物体所做的功即是表示力的向量和表示位移的向量的数量积.例4 已知力 与水平方向的夹角为30°(斜向上),
大小为50 N,一个质量为8 kg的木块受力 的作用在
动摩擦因数μ=0.02的水平平面上运动了20 m.问力
和摩擦力 所做的功分别为多少?(g=10 m/s2)向量解决物理问题方法:
1.将物理中的矢量用向量表示.
2.找出向量与向量的夹角.
3.利用向量的数量积计算功.1.证明直径所对的圆周角是直角.如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点,不与AB重合.求证
∠ACB=90°.证明:设 则 ,
由此可得:即 , ∠ACB=90°.思路分析本题方法:
1.计算速度的合速度.
2.计算时间必须使速度的方向和位移的方向一致.答:行驶航程最短时,所用的时间是3.1 min.注意:用该公式时应先将直线方程化为一般式. 1.点到直线的距离公式: ,2.掌握用向量方法解决平面几何问题的三个步骤:不奋苦而求速效,只落得少日浮夸,老来窘隘而已.
——郑板桥
