3.2.1 两角差的余弦函数 课件1
文档属性
| 名称 | 3.2.1 两角差的余弦函数 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
3.2.1 两角差的余弦函数
第三章 三角恒等变换
学习目标
1.通过实例理解两角差的余弦公式的推导过程。
2掌握两角差公式的运用
引入课题
思考1:一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
引入课题
sin60°
sin120°
cos60°
cos120°
cos(120°-60°)
sin30°
sin60°
cos30°
cos60°
cos(60°-30°)
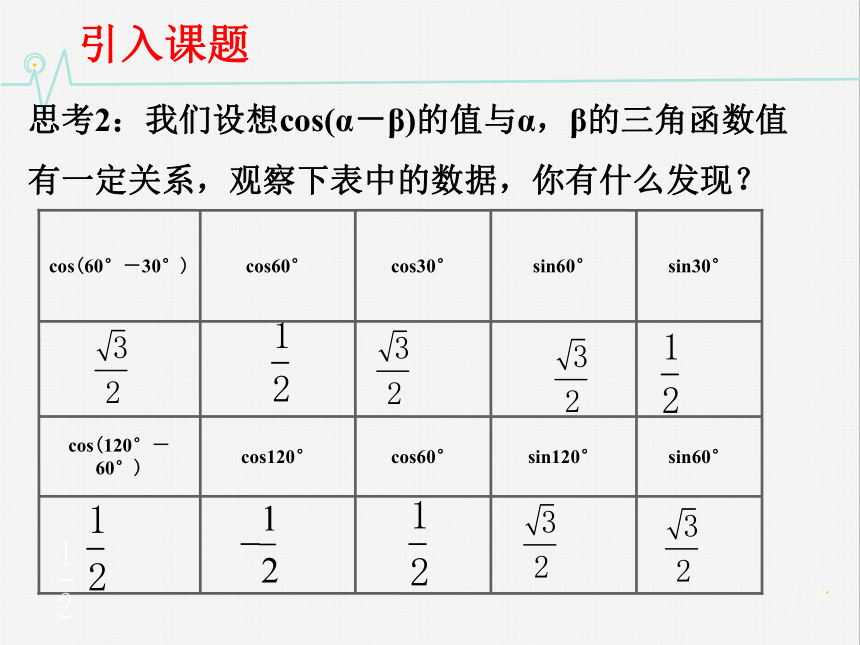
思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?
想一想
一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
探究点1
两角差的余弦公式
公式 cos(α-β)=_______________________
简记符号 C(α-β)
使用条件 α,β为任意角
cos αcos β+sin αsin β
探究点2 由三角函数值求角
设A,B为锐角△ABC的两个内角,向量a=(2cos A,2sin A),b=(3cos B,3sin B).若a,b的夹角为60°,求A-B的值.
探究点2 由三角函数值求角
探究点2 由三角函数值求角
【点评】 解这类问题一般分三步:第一步,求角的某一三角函数值;第二步,确定角所在的范围;第三步,根据角的范围写出所求角.
探究点3 给角求值
计算:(1)cos(-15°);
(2)cos 80°cos 35°+cos 10°cos 55°.
探究点3 给角求值
探究点3 给角求值
【点评】
(1)对于角度大的式子的化简问题,应先根据诱导公式将角度化小(一般是化成锐角).
(2)在应用差角的余弦公式求值时,逆用公式是十分常见的,要注意培养这种能力.
典型例题
向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论?
B
O
A
x
y
α
β
θ
α=2kπ+β+θ或β=2kπ+α+θ
cos(α-β)=cosαcosβ+sinαsinβ
课堂练习
若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么?
课堂练习
x
y
P
P1
M
B
O
A
C
+
1
1
课堂小结
1.两角差的余弦公式中,α、β可以是单个角,也可以是两个角的和或差,在运用公式时常将两角的和或差视为一个整体.
2.在两角差的余弦公式的求值应用中,一般思路是:
(1)把非特殊角转化为特殊角的和或差,利用公式直接求值.
(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.
3.2.1 两角差的余弦函数
第三章 三角恒等变换
学习目标
1.通过实例理解两角差的余弦公式的推导过程。
2掌握两角差公式的运用
引入课题
思考1:一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
引入课题
sin60°
sin120°
cos60°
cos120°
cos(120°-60°)
sin30°
sin60°
cos30°
cos60°
cos(60°-30°)
思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?
想一想
一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
探究点1
两角差的余弦公式
公式 cos(α-β)=_______________________
简记符号 C(α-β)
使用条件 α,β为任意角
cos αcos β+sin αsin β
探究点2 由三角函数值求角
设A,B为锐角△ABC的两个内角,向量a=(2cos A,2sin A),b=(3cos B,3sin B).若a,b的夹角为60°,求A-B的值.
探究点2 由三角函数值求角
探究点2 由三角函数值求角
【点评】 解这类问题一般分三步:第一步,求角的某一三角函数值;第二步,确定角所在的范围;第三步,根据角的范围写出所求角.
探究点3 给角求值
计算:(1)cos(-15°);
(2)cos 80°cos 35°+cos 10°cos 55°.
探究点3 给角求值
探究点3 给角求值
【点评】
(1)对于角度大的式子的化简问题,应先根据诱导公式将角度化小(一般是化成锐角).
(2)在应用差角的余弦公式求值时,逆用公式是十分常见的,要注意培养这种能力.
典型例题
向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论?
B
O
A
x
y
α
β
θ
α=2kπ+β+θ或β=2kπ+α+θ
cos(α-β)=cosαcosβ+sinαsinβ
课堂练习
若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么?
课堂练习
x
y
P
P1
M
B
O
A
C
+
1
1
课堂小结
1.两角差的余弦公式中,α、β可以是单个角,也可以是两个角的和或差,在运用公式时常将两角的和或差视为一个整体.
2.在两角差的余弦公式的求值应用中,一般思路是:
(1)把非特殊角转化为特殊角的和或差,利用公式直接求值.
(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.
