3.2.1 两角差的余弦函数 课件2
文档属性
| 名称 | 3.2.1 两角差的余弦函数 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 841.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览











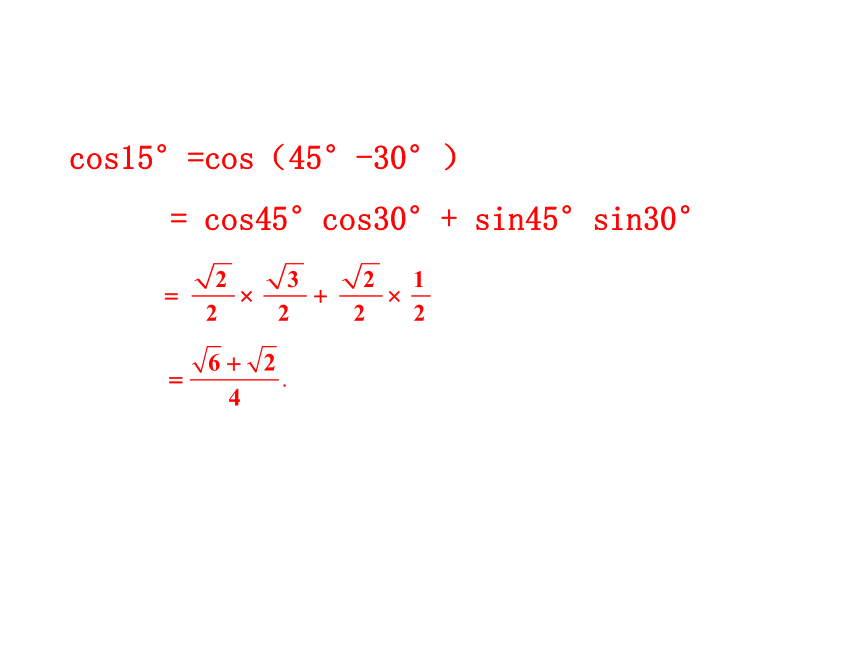
文档简介
课件34张PPT。3.2.1 两角差的余弦函数2.若 是单位向量,则1.平面向量的数量积3.平面向量的数量积的坐标运算4.写出五组诱导公式 规律小结:函数名不变,
符号看象限思考1:15?能否写成两个特殊角的和或差的形式? 如何求cos(–375?)的值?解:cos(–375?)=cos375?=cos(360?+15?)=cos15?思考2: cos15?=cos(45?-30?)=cos45?-cos30?成立吗?15?=45?-30?所以cos(45? -30?)≠cos45? -cos30?.
所以 cos(α+β)=cosα+cosβ不总是成立.思考3:究竟cos15?=?思考4:cos(45?-30?)能否用45?和30?的角的三角函数值来表示?思考5:如果能,那么一般情况下cos(α-β)能否用角α,β的三角函数值来表示?请进入本节课的学习!1.利用向量的数量积发现两角差的余弦公式.(重点)
2.能由两角差的余弦公式得到两角和的余弦公式和两角和与差的正弦公式.(难点)
3.灵活正反运用两角和与差的正弦、余弦函数.
(难点)探究点1 两角差的余弦函数在直角坐标系中,如图,以原点为中心,单位长度为半径作单位圆,又以原点为顶点,x轴非负半轴为始边分别作角α,β且α>β,我们首先研究α,β均为锐角的情况由图可知:单位圆上P1,P2两点,我们称上式为两角差的余弦公式,记作思考:公式cos(α-β)=cosαcosβ+sinαsinβ是否对任意角α,β都成立?
提示:当0≤α-β≤π时,公式显然成立;
当α-β不在[0,π]内时,利用诱导公式,存在θ∈[0,2π],使α-β=θ+2kπ,k∈Z,若θ∈[0,π],cosθ=cos(α-β);若θ∈(π,2π],2π-θ∈[0,π),cos(2π-θ)=cosθ=cos(α-β),故上述公式对任意角α,β都成立.注:1.公式中两边的符号正好相反(一正一负).2.式子右边同名三角函数相乘再加减,且余弦在前正弦在后.我们知道减去一个数等于加上这个数的相反数,利用诱导公式试求cos(α+β)?探究点2 两角和的余弦函数公式应用解 cos75°= cos(45°+30°)= cos45°cos30°-sin45°sin30°例1 不查表,求cos75°,cos15°的值.公式形式为ccss= cos45°cos30°+ sin45°sin30°cos15°=cos(45°-30°)技巧方法:
1.求α,β的正弦值、余弦值,注
意α,β的取值范围.
2.代入公式.例3 证明 ⑴cos( )=sinα(α为任意角). 所以 cos( )
=sinα.证明 ⑴ cos( )=cos cosα+sin sinα,因为 cos = 0,sin =1,⑵sin( )=cosα( 为任意角). (2) sin( )=cos[ -( )]
=cosα,所以sin( )=cosα.用类似的证法,可得:
⑶cos ( )=-sinα ⑷sin ( ) = cosα⑺cos( )=sinα ⑻sin ( ) =-cosα⑸ cos ( )=-sinα ⑹sin ( )=-cosα小结: , 角的三角函数值等于 的异名函数前加上把 看作锐角时原函数值的符号.探究点3 两角和与差的正弦函数2.两角差的正弦公式简记:简记:【提升总结】公式 的结构特征
(1) 的结构特征:左边是两角和、差的正弦,右边是前一角的正弦与后一角余弦的积与前一角的余弦与后一角正弦的积的和、差.
(2)公式中的角α,β是任意的角.令化 为一个角的三角函数形式把下列各式化为一个角的三角函数形式【变式练习】....【提升总结】灵活应用公式求三角函数值的三个注意点
(1)公式应用时要注意区分已知与未知的差别,利用角的分解与组合建立它们之间的联系.
(2)求三角函数值时要注意利用平方关系,并注意角的取值范围.
(3)注意题目中的隐含条件,如解决三角形问题时,要注意三角形内角和等于180°这一暗含条件.1.cos50°cos20°+sin50°sin20°的值为( )
A. B. C. D.
解析:cos50°cos20°+sin50°sin20°
=cos(50°-20°)=cos30°= .CA3.cos255°cos195°-sin75°sin195°=______.
解析:cos255°cos195°-sin75°sin195°
=cos75°cos15°+sin75°sin15°
=cos(75°-15°)
= .解:5.化简:本节课主要学习了:
1.
2.利用公式可以求非特殊角的三角函数值,化简 三角函数式和证明三角恒等式.应用公式时要灵活使用,并要注意公式的逆向使用.;;;.3.在用已知角来求未知角这类题型时,应注意两点:
(1)凑角,即尽可能用已知角表示未知角.
(2)角的范围,它决定符号取正、负的问题.化 为一个角的三角函数形式4..读书好似爬山,爬得越高,望得越远;读书好似耕耘,汗水流得越多,收获越丰满.
——臧克家
符号看象限思考1:15?能否写成两个特殊角的和或差的形式? 如何求cos(–375?)的值?解:cos(–375?)=cos375?=cos(360?+15?)=cos15?思考2: cos15?=cos(45?-30?)=cos45?-cos30?成立吗?15?=45?-30?所以cos(45? -30?)≠cos45? -cos30?.
所以 cos(α+β)=cosα+cosβ不总是成立.思考3:究竟cos15?=?思考4:cos(45?-30?)能否用45?和30?的角的三角函数值来表示?思考5:如果能,那么一般情况下cos(α-β)能否用角α,β的三角函数值来表示?请进入本节课的学习!1.利用向量的数量积发现两角差的余弦公式.(重点)
2.能由两角差的余弦公式得到两角和的余弦公式和两角和与差的正弦公式.(难点)
3.灵活正反运用两角和与差的正弦、余弦函数.
(难点)探究点1 两角差的余弦函数在直角坐标系中,如图,以原点为中心,单位长度为半径作单位圆,又以原点为顶点,x轴非负半轴为始边分别作角α,β且α>β,我们首先研究α,β均为锐角的情况由图可知:单位圆上P1,P2两点,我们称上式为两角差的余弦公式,记作思考:公式cos(α-β)=cosαcosβ+sinαsinβ是否对任意角α,β都成立?
提示:当0≤α-β≤π时,公式显然成立;
当α-β不在[0,π]内时,利用诱导公式,存在θ∈[0,2π],使α-β=θ+2kπ,k∈Z,若θ∈[0,π],cosθ=cos(α-β);若θ∈(π,2π],2π-θ∈[0,π),cos(2π-θ)=cosθ=cos(α-β),故上述公式对任意角α,β都成立.注:1.公式中两边的符号正好相反(一正一负).2.式子右边同名三角函数相乘再加减,且余弦在前正弦在后.我们知道减去一个数等于加上这个数的相反数,利用诱导公式试求cos(α+β)?探究点2 两角和的余弦函数公式应用解 cos75°= cos(45°+30°)= cos45°cos30°-sin45°sin30°例1 不查表,求cos75°,cos15°的值.公式形式为ccss= cos45°cos30°+ sin45°sin30°cos15°=cos(45°-30°)技巧方法:
1.求α,β的正弦值、余弦值,注
意α,β的取值范围.
2.代入公式.例3 证明 ⑴cos( )=sinα(α为任意角). 所以 cos( )
=sinα.证明 ⑴ cos( )=cos cosα+sin sinα,因为 cos = 0,sin =1,⑵sin( )=cosα( 为任意角). (2) sin( )=cos[ -( )]
=cosα,所以sin( )=cosα.用类似的证法,可得:
⑶cos ( )=-sinα ⑷sin ( ) = cosα⑺cos( )=sinα ⑻sin ( ) =-cosα⑸ cos ( )=-sinα ⑹sin ( )=-cosα小结: , 角的三角函数值等于 的异名函数前加上把 看作锐角时原函数值的符号.探究点3 两角和与差的正弦函数2.两角差的正弦公式简记:简记:【提升总结】公式 的结构特征
(1) 的结构特征:左边是两角和、差的正弦,右边是前一角的正弦与后一角余弦的积与前一角的余弦与后一角正弦的积的和、差.
(2)公式中的角α,β是任意的角.令化 为一个角的三角函数形式把下列各式化为一个角的三角函数形式【变式练习】....【提升总结】灵活应用公式求三角函数值的三个注意点
(1)公式应用时要注意区分已知与未知的差别,利用角的分解与组合建立它们之间的联系.
(2)求三角函数值时要注意利用平方关系,并注意角的取值范围.
(3)注意题目中的隐含条件,如解决三角形问题时,要注意三角形内角和等于180°这一暗含条件.1.cos50°cos20°+sin50°sin20°的值为( )
A. B. C. D.
解析:cos50°cos20°+sin50°sin20°
=cos(50°-20°)=cos30°= .CA3.cos255°cos195°-sin75°sin195°=______.
解析:cos255°cos195°-sin75°sin195°
=cos75°cos15°+sin75°sin15°
=cos(75°-15°)
= .解:5.化简:本节课主要学习了:
1.
2.利用公式可以求非特殊角的三角函数值,化简 三角函数式和证明三角恒等式.应用公式时要灵活使用,并要注意公式的逆向使用.;;;.3.在用已知角来求未知角这类题型时,应注意两点:
(1)凑角,即尽可能用已知角表示未知角.
(2)角的范围,它决定符号取正、负的问题.化 为一个角的三角函数形式4..读书好似爬山,爬得越高,望得越远;读书好似耕耘,汗水流得越多,收获越丰满.
——臧克家
