3.2.3 两角和与差的正切函数 课件3
文档属性
| 名称 | 3.2.3 两角和与差的正切函数 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览










文档简介
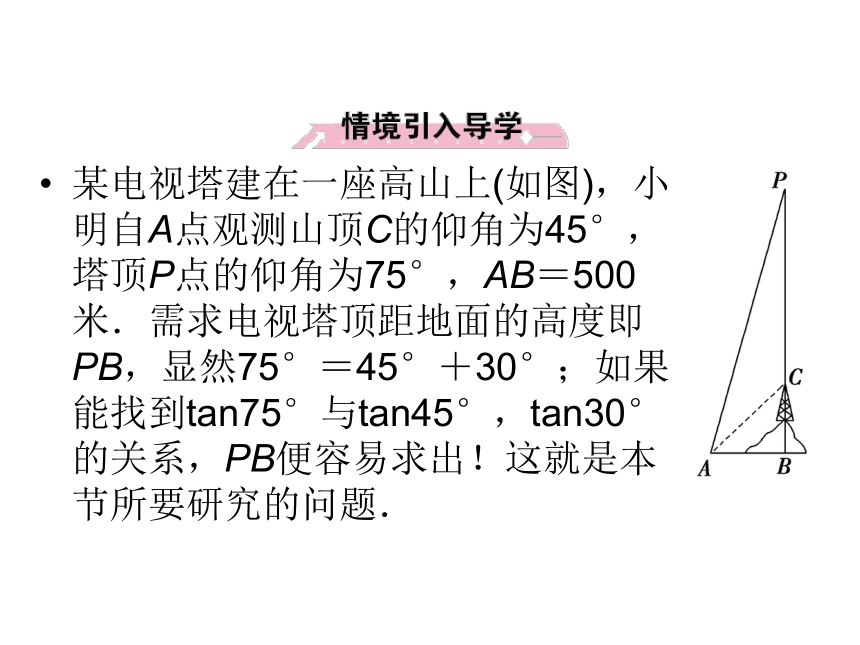
课件41张PPT。三角恒等变形第三章第三章3.2.3 两角和与差的正切函数某电视塔建在一座高山上(如图),小明自A点观测山顶C的仰角为45°,塔顶P点的仰角为75°,AB=500米.需求电视塔顶距地面的高度即PB,显然75°=45°+30°;如果能找到tan75°与tan45°,tan30°的关系,PB便容易求出!这就是本节所要研究的问题.[答案] B[答案] A[答案] B4.若tanα=2,tan(β-α)=3,则tan(β-2α)的值为________.5.设tanα,tanβ是方程x2-3x+2=0的两根,则tan(α+β)的值为________.
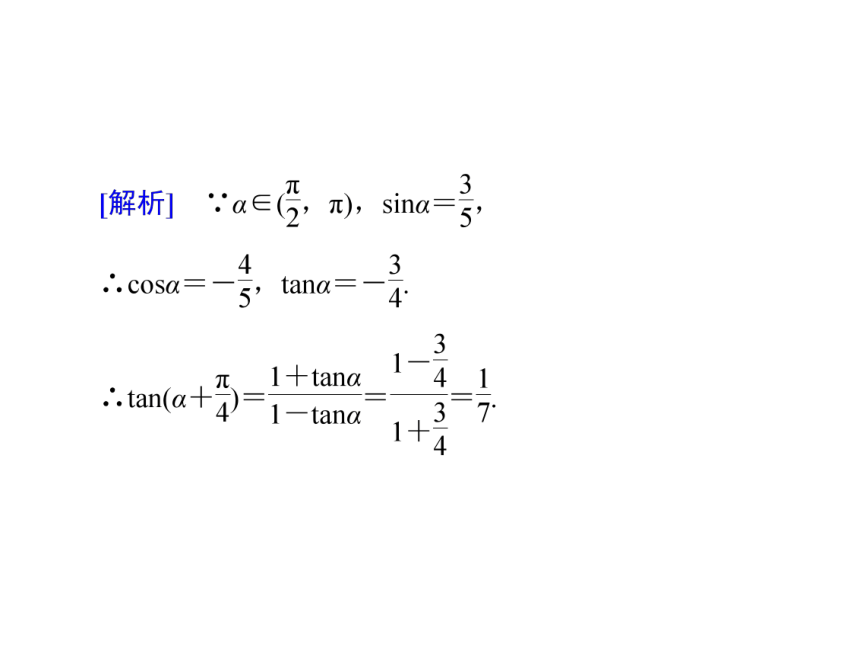
[答案] -3公式的直接应用
[规律总结] 该题属于给值求值题,解答此题的关键在于先用Tα±β公式分析一下待求的问题需要什么,然后利用化归的思想,把未知的向已知进行转化.解题过程中须多加注意角的范围,必要时实行拆分角.公式的逆用与变形用[思路分析] 先求出tanα及tan2β的值,再求出tan(α+2β)的值,后依据α+2β范围判断α+2β的大小.给值求角
[规律总结] 在给值求角时,一般先求所要求角的一个三角函数值,再根据题设确定角的范围,利用三角函数的单调性求出角,确定角的范围是关键,一定要使所选的函数在此范围内单调.[思路分析] 利用tanα+tanβ=tan(α+β)(1-tanα tanβ) 将所给的等式变形.公式的综合应用在△ABC中,已知tanA与tanB是方程2x2+9x-13=0的两个根,求tanC的值.
[答案] -3公式的直接应用
[规律总结] 该题属于给值求值题,解答此题的关键在于先用Tα±β公式分析一下待求的问题需要什么,然后利用化归的思想,把未知的向已知进行转化.解题过程中须多加注意角的范围,必要时实行拆分角.公式的逆用与变形用[思路分析] 先求出tanα及tan2β的值,再求出tan(α+2β)的值,后依据α+2β范围判断α+2β的大小.给值求角
[规律总结] 在给值求角时,一般先求所要求角的一个三角函数值,再根据题设确定角的范围,利用三角函数的单调性求出角,确定角的范围是关键,一定要使所选的函数在此范围内单调.[思路分析] 利用tanα+tanβ=tan(α+β)(1-tanα tanβ) 将所给的等式变形.公式的综合应用在△ABC中,已知tanA与tanB是方程2x2+9x-13=0的两个根,求tanC的值.
