3.3 二倍角的三角函数 课件

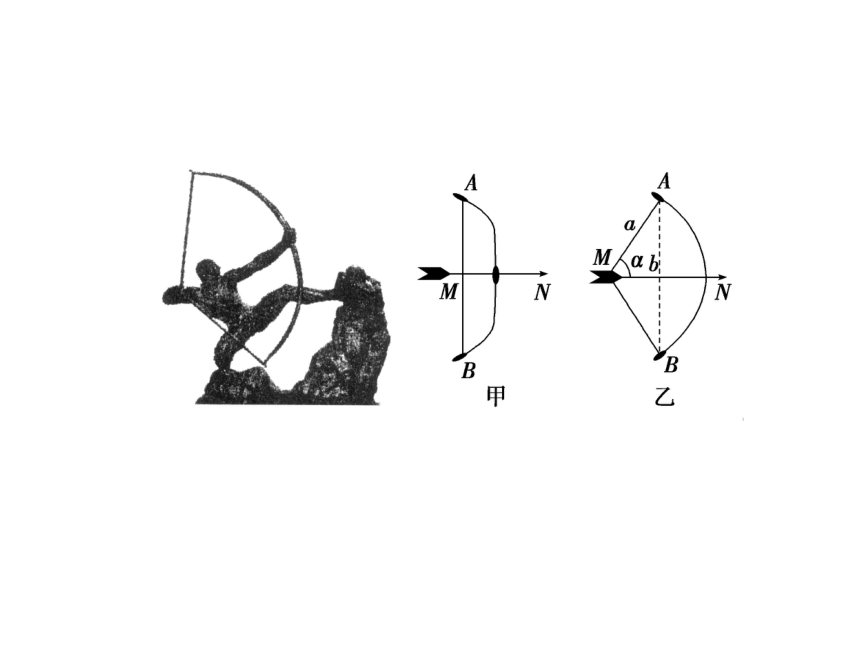
课件48张PPT。三角恒等变形第三章3.3 二倍角的三角函数第三章如图甲所示，已知弓弦的长度AB＝2a，弓箭的长度MN＝2b(其中MA＝MB，MN⊥AB)．假设拉满弓时，箭头和箭尾到A，B的连线的距离相等(如图乙所示)，设∠AMN＝α，你能用a，b表示∠AMB的正切值，即tan2α的值吗？
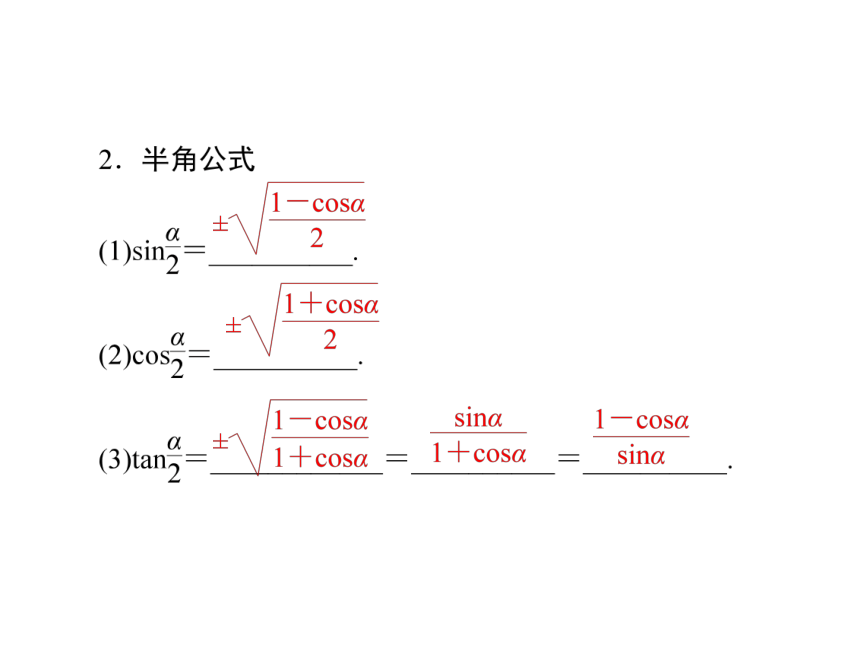
tan2α与tanα之间存在怎样的关系呢？现在我们来学习二倍角与半角公式的知识．2sinαcosα cos2α－sin2αcos2α－sin2α2cos2α－1 1－2sin2α [答案]　B[答案]　B[答案]　C4．函数y＝sin2xcos2x的最小正周期是________，最大值是________．利用倍角公式求值[思路分析]　本题主要是倍角公式的逆用，关键是搞清公式的特征．
[规律总结]　解答此类题目一方面要注意角的倍数关系，另一方面要注意函数名称的转化方法，同角三角函数的关系及诱导公式是常用的方法．[答案]　(1)C　(2)B　(3)D利用公式化简与证明半角公式的应用三角公式与三角函数的图像与性质的综合应用 [思路分析]　先求出a·b，再利用倍角公式及降幂公式将f(x)化成Asin(ωx＋φ)＋k的形式，进而研究函数的性质．
[规律总结]　解答此类综合题的关键是利用三角函数的和、差、倍、半角公式化为f(x)＝Asin(ωx＋φ)＋k的形式，然后借助于三角函数的图像及性质去研究f(x)的相应性质，解答过程中一定要注意公式的合理应用，以免错用公式，导致化简失误．