27.2.1相似三角形的判定定理1,2(第2课时)课文练习含答案
文档属性
| 名称 | 27.2.1相似三角形的判定定理1,2(第2课时)课文练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 67.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 15:54:45 | ||
图片预览

文档简介
第2课时 相似三角形的判定定理1,2
基础题
知识点1 三边成比例的两个三角形相似
1.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
2.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁4点中的( )
A.甲
B.乙
C.丙
D.丁
3.若△ABC各边分别为AB=10
cm,BC=8
cm,AC=6
cm,△DEF的两边为DE=5
cm,EF=4
cm,则当DF=______cm时,△ABC∽△DEF.
4.试判断图中的两个三角形是否相似,并说明理由.
知识点2 两边成比例且夹角相等的两个三角形相似
5.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
6.在等边三角形ABC中,D、E分别在AC、AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
7.根据下列条件,判断△ABC和△A′B′C′是否相似,并说明理由.
∠B=50°,AB=2,BC=3,∠B′=50°,A′B′=12,B′C′=18.
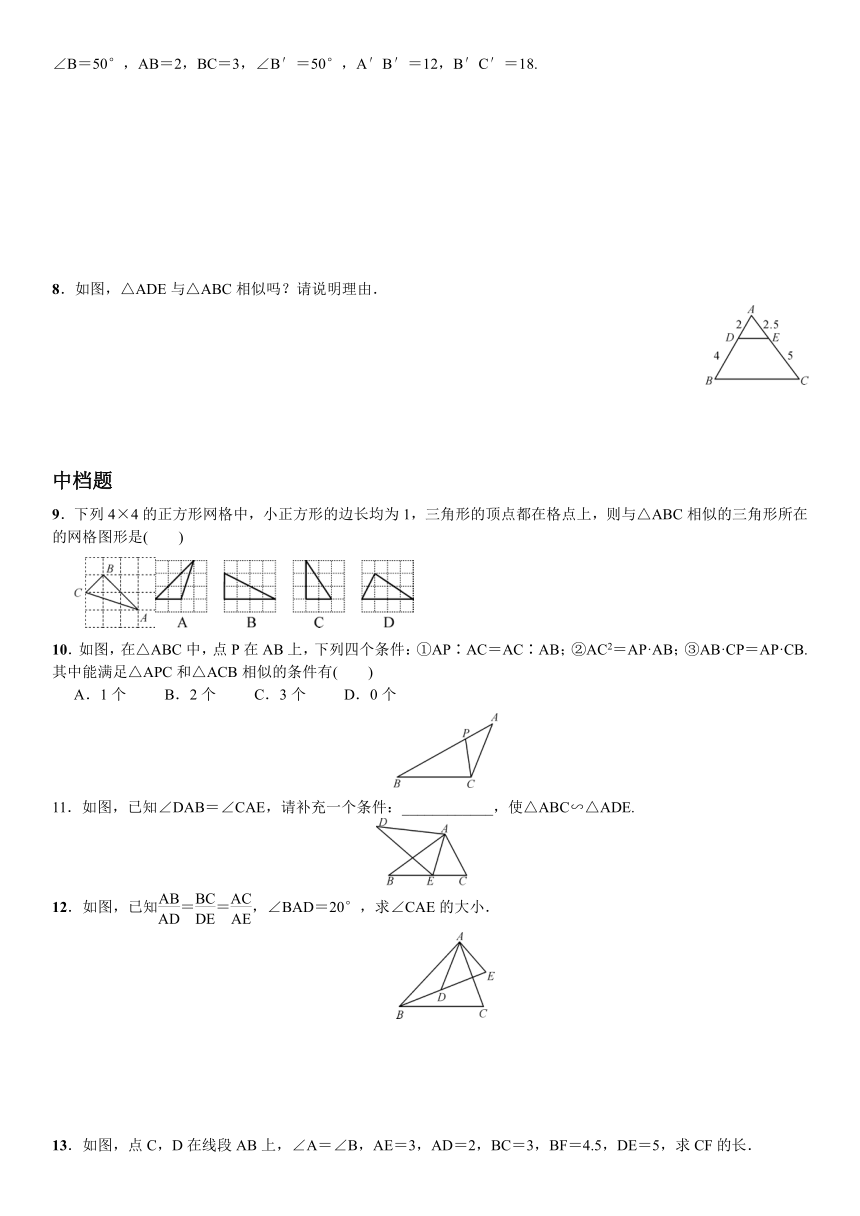
8.如图,△ADE与△ABC相似吗?请说明理由.
中档题
9.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
10.如图,在△ABC中,点P在AB上,下列四个条件:①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件有( )
A.1个
B.2个
C.3个
D.0个
11.如图,已知∠DAB=∠CAE,请补充一个条件:____________,使△ABC∽△ADE.
12.如图,已知==,∠BAD=20°,求∠CAE的大小.
13.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
14.已知:如图,在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:△ADB∽△EAC.
15.已知如图,正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
综合题
16.(宿迁中考改编)如图,
AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A.1个
B.2个
C.3个
D.4个
参考答案
1.A 2.C 3.3
4.相似.理由如下:在Rt△ABC中,BC===1.8,
在Rt△DEF中,DF===4.8,
∴===,∴△ABC∽△DEF.
5.C 6.B
7.相似.理由:∵==,==,
∴=.∵∠B=∠B′,∴△ABC∽△A′B′C′.
8.△ADE与△ABC相似.
理由:∵==,==,∴=.
∵∠A=∠A,∴△ADE∽△ABC.
9.B 10.B 11.=
12.∵==,∴△ABC∽△ADE.∴∠BAC=∠DAE.
又∠DAC是公共角,∴∠CAE=∠BAD=20°.
13.∵==,=,∴=.
又∠A=∠B,∴△AED∽△BFC,
∴=.∴=.∴CF=.
14.证明:∵AB=AC,∴∠ABC=∠ACB,∴∠ABD=∠ACE.
∵AB2=DB·CE,∴=.
又AB=AC,∴=.∴△ADB∽△EAC.
15.证明:设正方形的边长为4a,则AD=CD=BC=4a.
∵Q是CD的中点,BP=3PC,∴DQ=CQ=2a,PC=a.
∴==.
又∵∠D=∠C=90°,∴△ADQ∽△QCP.
16.C
基础题
知识点1 三边成比例的两个三角形相似
1.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
2.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁4点中的( )
A.甲
B.乙
C.丙
D.丁
3.若△ABC各边分别为AB=10
cm,BC=8
cm,AC=6
cm,△DEF的两边为DE=5
cm,EF=4
cm,则当DF=______cm时,△ABC∽△DEF.
4.试判断图中的两个三角形是否相似,并说明理由.
知识点2 两边成比例且夹角相等的两个三角形相似
5.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
6.在等边三角形ABC中,D、E分别在AC、AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
7.根据下列条件,判断△ABC和△A′B′C′是否相似,并说明理由.
∠B=50°,AB=2,BC=3,∠B′=50°,A′B′=12,B′C′=18.
8.如图,△ADE与△ABC相似吗?请说明理由.
中档题
9.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
10.如图,在△ABC中,点P在AB上,下列四个条件:①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件有( )
A.1个
B.2个
C.3个
D.0个
11.如图,已知∠DAB=∠CAE,请补充一个条件:____________,使△ABC∽△ADE.
12.如图,已知==,∠BAD=20°,求∠CAE的大小.
13.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
14.已知:如图,在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:△ADB∽△EAC.
15.已知如图,正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
综合题
16.(宿迁中考改编)如图,
AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A.1个
B.2个
C.3个
D.4个
参考答案
1.A 2.C 3.3
4.相似.理由如下:在Rt△ABC中,BC===1.8,
在Rt△DEF中,DF===4.8,
∴===,∴△ABC∽△DEF.
5.C 6.B
7.相似.理由:∵==,==,
∴=.∵∠B=∠B′,∴△ABC∽△A′B′C′.
8.△ADE与△ABC相似.
理由:∵==,==,∴=.
∵∠A=∠A,∴△ADE∽△ABC.
9.B 10.B 11.=
12.∵==,∴△ABC∽△ADE.∴∠BAC=∠DAE.
又∠DAC是公共角,∴∠CAE=∠BAD=20°.
13.∵==,=,∴=.
又∠A=∠B,∴△AED∽△BFC,
∴=.∴=.∴CF=.
14.证明:∵AB=AC,∴∠ABC=∠ACB,∴∠ABD=∠ACE.
∵AB2=DB·CE,∴=.
又AB=AC,∴=.∴△ADB∽△EAC.
15.证明:设正方形的边长为4a,则AD=CD=BC=4a.
∵Q是CD的中点,BP=3PC,∴DQ=CQ=2a,PC=a.
∴==.
又∵∠D=∠C=90°,∴△ADQ∽△QCP.
16.C
