27.2.1相似三角形的判定定理3(第3课时)课文练习含答案
文档属性
| 名称 | 27.2.1相似三角形的判定定理3(第3课时)课文练习含答案 | 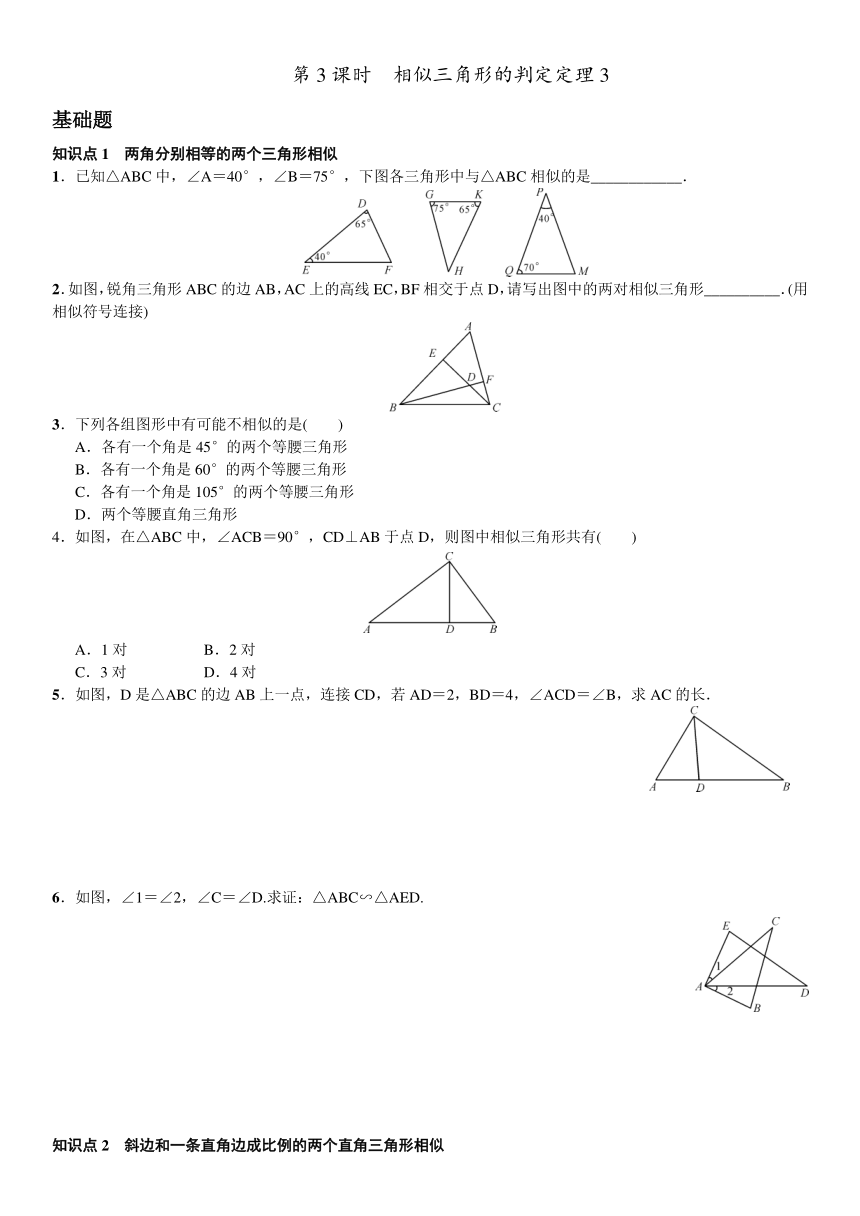 | |
| 格式 | zip | ||
| 文件大小 | 56.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 15:56:07 | ||
图片预览


文档简介
第3课时 相似三角形的判定定理3
基础题
知识点1 两角分别相等的两个三角形相似
1.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是____________.
2.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形__________.(用相似符号连接)
3.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
5.如图,D是△ABC的边AB上一点,连接CD,若AD=2,BD=4,∠ACD=∠B,求AC的长.
21世纪教育网
6.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
知识点2 斜边和一条直角边成比例的两个直角三角形相似
7.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′=________时,△ABC∽△A′B′C′.
8.一个直角三角形的一条直角边长和斜边长
( http: / / www.21cnjy.com )分别为8
cm和15
cm,另一个直角三角形的一条直角边长和斜边长分别是6
cm和
cm,这两个直角三角形________(填“是”或“不是”)相似三角形.
9.一个直角三角形的两边长分别为3和6,另
( http: / / www.21cnjy.com )一个直角三角形的两边长分别为2和4,那么这两个直角三角形________(填“一定”“不一定”或“一定不”)相似.
10.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.
中档题
11.(毕节中考)如图,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A.
B.
C.
D.
12.(贵阳中考)如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1
B.P2
C.P3
D.P4
13.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,求AB的长度.21世纪教育网
21世纪教育网
14.已知:∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
15.(滨州中考改编)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC
综合题
16.如图,在△ABC中,AD、BF分别是
( http: / / www.21cnjy.com )BC、AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H,求证:DE2=EG·EH.
参考答案
1.△EFD,△HGK 2.答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等 3.A 4.C
5.在△ABC和△ACD中,∵∠ACD=∠B,∠A=∠A,
∴△ABC∽△ACD.∴=.
∴AC2=AD·AB=2×6=12.∴AC=2.
6.证明:∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠EAD.
又∵∠C=∠D,∴△ABC∽△AED.
7.10 8.是 9.不一定
10.∵四边形ABCD是正方形,M为CD中点,∴CM=MD=AD.21世纪教育网
∵BP=3PC,∴PC=BC=AD=CM.∴==.
∵∠PCM=∠ADM=90°,∴△MCP∽△ADM.
11.A 12.
C
13.∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,∴∠A+∠ACB=90°.
∵AC⊥CE,∴∠ACE=90°.∴∠ACB+∠ECD=90°
.∴∠A=∠ECD.∴△ABC∽△CDE.∴=.
又∵C是线段BD的中点,BD=4,
∴BC=CD=2.∴=,即AB=4.
14.①若△ABC∽△ADB,则=.∴AD=3;
②若△ABC∽△DAB,则=.∴AD=3.
综上所述,当AD=3或3时,两直角三角形相似.
15.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,∴△APQ∽△CDQ.
(2)当DP⊥AC时,∠QCD+∠QDC=90°.
∵∠ADQ+∠QDC=90°,∴∠DCA=∠ADP.
又∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD.∴=,∴=,解得PA=5.∴t=5. 21世纪教育网
16.证明:∵AD、BF分别是BC、AC边上高,∴∠ADB=∠BED=90°
.∴∠EBD+∠EDB=∠EDB+∠ADE.∴∠EBD=∠EDA.
∴△AED∽△DEB.∴DE2=AE·BE.
又∵∠HFG=90°,∠BGE=∠HGF,
∴∠EBG=∠H.
∵∠BEG=∠HEA=90°,
∴△BEG∽△HEA.
∴=,
即EG·EH=AE·BE.∴DE2=EG·EH.
基础题
知识点1 两角分别相等的两个三角形相似
1.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是____________.
2.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形__________.(用相似符号连接)
3.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
4.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
5.如图,D是△ABC的边AB上一点,连接CD,若AD=2,BD=4,∠ACD=∠B,求AC的长.
21世纪教育网
6.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
知识点2 斜边和一条直角边成比例的两个直角三角形相似
7.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′=________时,△ABC∽△A′B′C′.
8.一个直角三角形的一条直角边长和斜边长
( http: / / www.21cnjy.com )分别为8
cm和15
cm,另一个直角三角形的一条直角边长和斜边长分别是6
cm和
cm,这两个直角三角形________(填“是”或“不是”)相似三角形.
9.一个直角三角形的两边长分别为3和6,另
( http: / / www.21cnjy.com )一个直角三角形的两边长分别为2和4,那么这两个直角三角形________(填“一定”“不一定”或“一定不”)相似.
10.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.
中档题
11.(毕节中考)如图,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长等于( )
A.
B.
C.
D.
12.(贵阳中考)如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A.P1
B.P2
C.P3
D.P4
13.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,求AB的长度.21世纪教育网
21世纪教育网
14.已知:∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
15.(滨州中考改编)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC
综合题
16.如图,在△ABC中,AD、BF分别是
( http: / / www.21cnjy.com )BC、AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H,求证:DE2=EG·EH.
参考答案
1.△EFD,△HGK 2.答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等 3.A 4.C
5.在△ABC和△ACD中,∵∠ACD=∠B,∠A=∠A,
∴△ABC∽△ACD.∴=.
∴AC2=AD·AB=2×6=12.∴AC=2.
6.证明:∵∠1=∠2,∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠EAD.
又∵∠C=∠D,∴△ABC∽△AED.
7.10 8.是 9.不一定
10.∵四边形ABCD是正方形,M为CD中点,∴CM=MD=AD.21世纪教育网
∵BP=3PC,∴PC=BC=AD=CM.∴==.
∵∠PCM=∠ADM=90°,∴△MCP∽△ADM.
11.A 12.
C
13.∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,∴∠A+∠ACB=90°.
∵AC⊥CE,∴∠ACE=90°.∴∠ACB+∠ECD=90°
.∴∠A=∠ECD.∴△ABC∽△CDE.∴=.
又∵C是线段BD的中点,BD=4,
∴BC=CD=2.∴=,即AB=4.
14.①若△ABC∽△ADB,则=.∴AD=3;
②若△ABC∽△DAB,则=.∴AD=3.
综上所述,当AD=3或3时,两直角三角形相似.
15.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,∴△APQ∽△CDQ.
(2)当DP⊥AC时,∠QCD+∠QDC=90°.
∵∠ADQ+∠QDC=90°,∴∠DCA=∠ADP.
又∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD.∴=,∴=,解得PA=5.∴t=5. 21世纪教育网
16.证明:∵AD、BF分别是BC、AC边上高,∴∠ADB=∠BED=90°
.∴∠EBD+∠EDB=∠EDB+∠ADE.∴∠EBD=∠EDA.
∴△AED∽△DEB.∴DE2=AE·BE.
又∵∠HFG=90°,∠BGE=∠HGF,
∴∠EBG=∠H.
∵∠BEG=∠HEA=90°,
∴△BEG∽△HEA.
∴=,
即EG·EH=AE·BE.∴DE2=EG·EH.
