27.2.2相似三角形的性质 课文练习含答案
文档属性
| 名称 | 27.2.2相似三角形的性质 课文练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 51.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览

文档简介
27.2.2 相似三角形的性质
基础题
知识点1 相似三角形对应线段的比等于相似比
1.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( )
A.1∶4
B.1∶3
C.1∶
D.1∶2
2.如图,△ABC∽△A′B′C′,相似比为3∶4,AD,A′D′分别是边BC,B′C′上的中线,则AD∶A′D′=______.
3.若△ABC∽△A′B′C′,AB=1
( http: / / www.21cnjy.com )6
cm,A′B′=4
cm,AD平分∠BAC,A′D′平分∠B′A′C′,A′D′=3
cm,则AD=______cm.
4.已知:△ABC∽△A′B′C′,AB=4
cm,A′B′=10
cm,AE是△ABC的一条高,AE=4.8
cm.求△A′B′C′中对应高线A′E′的长.
知识点2 相似三角形周长的比等于相似比
5.若△ABC∽△A′B′C′,相似比为1∶3,则△ABC与△A′B′C′周长的比为( )
A.1∶3
B.3∶1
C.1∶9
D.9∶1
6.如图,在△ABC中,D,E分别是AB,AC上的点,DE∥BC,且AD=AB,则△ADE的周长与△ABC的周长的比为________.
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.求△BCD与△ABC的周长之比.
知识点3 相似三角形面积的比等于相似比的平方
8.(黔西南中考)已知△ABC∽△A′B′C′,且=,则S△ABC∶S△A′B′C′为( )
A.1∶2
B.2∶1
C.1∶4
D.4∶1
9.(广东中考)若两个相似三角形的周长比为2∶3,则它们的面积比是________.
10.(怀化中考)如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE∶S△ABC=________.
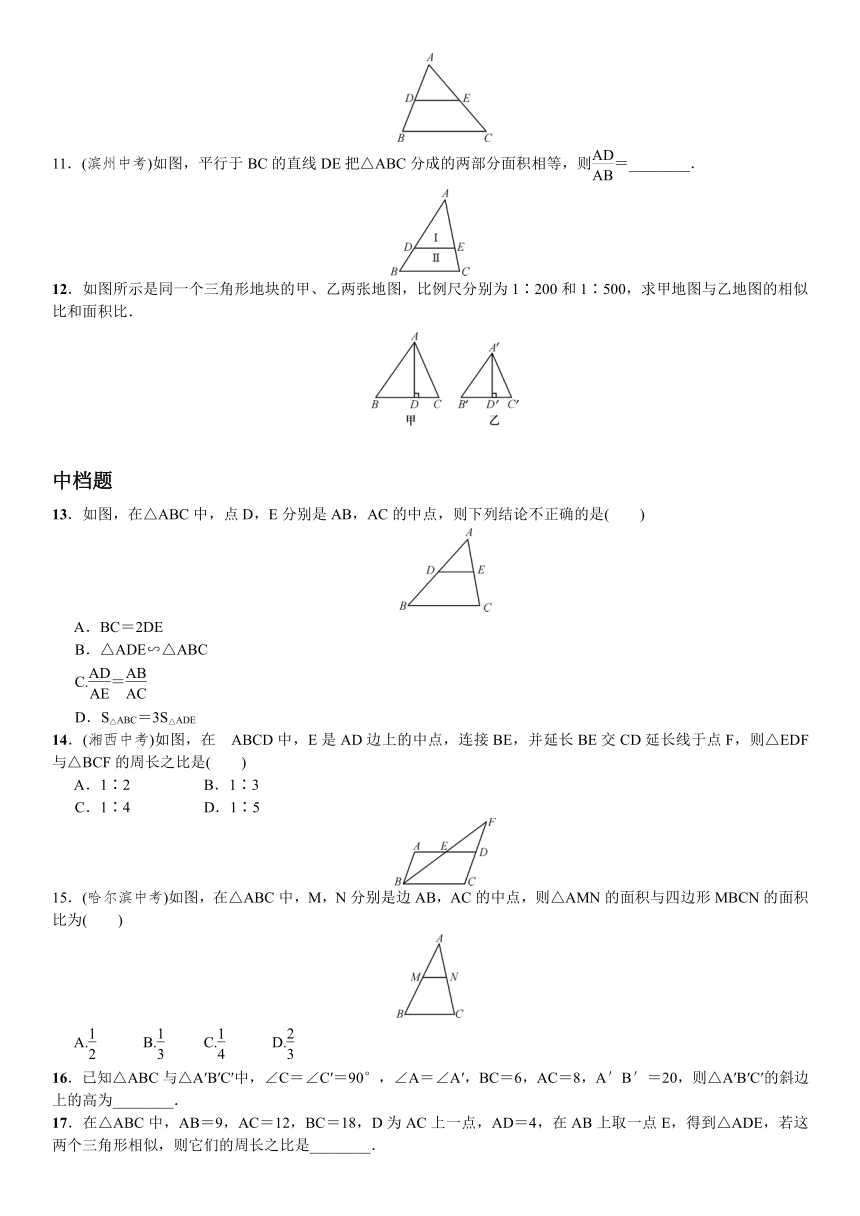
11.(滨州中考)如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________.
12.如图所示是同一个三角形地块的甲、乙两张地图,比例尺分别为1∶200和1∶500,求甲地图与乙地图的相似比和面积比.
中档题
13.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论不正确的是( )
A.BC=2DE
B.△ADE∽△ABC
C.=
D.S△ABC=3S△ADE
14.(湘西中考)如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
15.(哈尔滨中考)如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为( )
A.
B.
C.
D.
16.已知△ABC与△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,BC=6,AC=8,A′B′=20,则△A′B′C′的斜边上的高为________.
17.在△ABC中,AB=9,AC=12,BC=18,D为AC上一点,AD=4,在AB上取一点E,得到△ADE,若这两个三角形相似,则它们的周长之比是________.
18.如图,在△ABC中,D,E分别是△ABC的AB,AC边上的点,DE∥BC,CF,EG分别是△ABC与△ADE的中线,已知AD∶DB=4∶3,AB=18
cm,EG=4
cm,求CF的长.
19.已知△ABC∽△DEF,=,△ABC的周长是12
cm,面积是30
cm2.
(1)求△DEF的周长;
21世纪教育网
(2)求△DEF的面积.
21世纪教育网
21世纪教育网
综合题
20.如图,在△ABC中,DF∥EG∥BC
( http: / / www.21cnjy.com ),且AD=DE=EB,△ABC被DF、EG分成三部分,且三部分面积分别为S1,S2,S3,求S1∶S2∶S3的值.
参考答案
1.D 2.3∶4 3.12
4.∵△ABC∽△A′B′C′,21世纪教育网
∴=.∴=.∴A′E′=12
cm.
5.A 6.1∶3
7.∵∠B=∠B,∠BDC=∠BCA=90°
∴△BCD∽△BAC.
∴∠BCD=∠A=30°
在Rt△BCD中,∵∠BCD=30°,∴BC=2BD.
∵△BCD∽△BAC,∴C△BCD∶C△BAC=BD∶BC=1∶2.
8.C 9.4∶9 10.1∶4 11.
12.甲地图与乙地图的相似比==.面积的比为()2=.
13.D 14.A 15.B 16. 17.4∶9或1∶3
18.∵AD∶DB=4∶3,∴AD∶AB=4∶7.
∵DE∥BC,∴△ABC∽△ADE.
∵CF,EG分别是△ABC与△ADE的中线,
∴=.∴=.∴CF=7
cm..
19.(1)∵△ABC∽△DEF,=,∴△DEF的周长=12×=8
(cm).
(2)∵△ABC∽△DEF,=,∴△DEF的面积=30×()2=13(cm2).
20.∵DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC.
又∵AD=DE=EB,
∴三个三角形的相似比是1∶2∶3,21世纪教育网
∴面积的比是1∶4∶9,设△AEF的面积是a,则△AEG与△ABC的面积分别是4a,9a,
∴S2=3a,S3=5a,则S1∶S2∶S3=1∶3∶5
基础题
知识点1 相似三角形对应线段的比等于相似比
1.顺次连接三角形三边的中点,所成的三角形与原三角形对应高的比是( )
A.1∶4
B.1∶3
C.1∶
D.1∶2
2.如图,△ABC∽△A′B′C′,相似比为3∶4,AD,A′D′分别是边BC,B′C′上的中线,则AD∶A′D′=______.
3.若△ABC∽△A′B′C′,AB=1
( http: / / www.21cnjy.com )6
cm,A′B′=4
cm,AD平分∠BAC,A′D′平分∠B′A′C′,A′D′=3
cm,则AD=______cm.
4.已知:△ABC∽△A′B′C′,AB=4
cm,A′B′=10
cm,AE是△ABC的一条高,AE=4.8
cm.求△A′B′C′中对应高线A′E′的长.
知识点2 相似三角形周长的比等于相似比
5.若△ABC∽△A′B′C′,相似比为1∶3,则△ABC与△A′B′C′周长的比为( )
A.1∶3
B.3∶1
C.1∶9
D.9∶1
6.如图,在△ABC中,D,E分别是AB,AC上的点,DE∥BC,且AD=AB,则△ADE的周长与△ABC的周长的比为________.
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.求△BCD与△ABC的周长之比.
知识点3 相似三角形面积的比等于相似比的平方
8.(黔西南中考)已知△ABC∽△A′B′C′,且=,则S△ABC∶S△A′B′C′为( )
A.1∶2
B.2∶1
C.1∶4
D.4∶1
9.(广东中考)若两个相似三角形的周长比为2∶3,则它们的面积比是________.
10.(怀化中考)如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE∶S△ABC=________.
11.(滨州中考)如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________.
12.如图所示是同一个三角形地块的甲、乙两张地图,比例尺分别为1∶200和1∶500,求甲地图与乙地图的相似比和面积比.
中档题
13.如图,在△ABC中,点D,E分别是AB,AC的中点,则下列结论不正确的是( )
A.BC=2DE
B.△ADE∽△ABC
C.=
D.S△ABC=3S△ADE
14.(湘西中考)如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
15.(哈尔滨中考)如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为( )
A.
B.
C.
D.
16.已知△ABC与△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,BC=6,AC=8,A′B′=20,则△A′B′C′的斜边上的高为________.
17.在△ABC中,AB=9,AC=12,BC=18,D为AC上一点,AD=4,在AB上取一点E,得到△ADE,若这两个三角形相似,则它们的周长之比是________.
18.如图,在△ABC中,D,E分别是△ABC的AB,AC边上的点,DE∥BC,CF,EG分别是△ABC与△ADE的中线,已知AD∶DB=4∶3,AB=18
cm,EG=4
cm,求CF的长.
19.已知△ABC∽△DEF,=,△ABC的周长是12
cm,面积是30
cm2.
(1)求△DEF的周长;
21世纪教育网
(2)求△DEF的面积.
21世纪教育网
21世纪教育网
综合题
20.如图,在△ABC中,DF∥EG∥BC
( http: / / www.21cnjy.com ),且AD=DE=EB,△ABC被DF、EG分成三部分,且三部分面积分别为S1,S2,S3,求S1∶S2∶S3的值.
参考答案
1.D 2.3∶4 3.12
4.∵△ABC∽△A′B′C′,21世纪教育网
∴=.∴=.∴A′E′=12
cm.
5.A 6.1∶3
7.∵∠B=∠B,∠BDC=∠BCA=90°
∴△BCD∽△BAC.
∴∠BCD=∠A=30°
在Rt△BCD中,∵∠BCD=30°,∴BC=2BD.
∵△BCD∽△BAC,∴C△BCD∶C△BAC=BD∶BC=1∶2.
8.C 9.4∶9 10.1∶4 11.
12.甲地图与乙地图的相似比==.面积的比为()2=.
13.D 14.A 15.B 16. 17.4∶9或1∶3
18.∵AD∶DB=4∶3,∴AD∶AB=4∶7.
∵DE∥BC,∴△ABC∽△ADE.
∵CF,EG分别是△ABC与△ADE的中线,
∴=.∴=.∴CF=7
cm..
19.(1)∵△ABC∽△DEF,=,∴△DEF的周长=12×=8
(cm).
(2)∵△ABC∽△DEF,=,∴△DEF的面积=30×()2=13(cm2).
20.∵DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC.
又∵AD=DE=EB,
∴三个三角形的相似比是1∶2∶3,21世纪教育网
∴面积的比是1∶4∶9,设△AEF的面积是a,则△AEG与△ABC的面积分别是4a,9a,
∴S2=3a,S3=5a,则S1∶S2∶S3=1∶3∶5
