27.2.3相似三角形的应用举例 课文练习含答案
文档属性
| 名称 | 27.2.3相似三角形的应用举例 课文练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
27.2.3 相似三角形应用举例
基础题
知识点1 测量物高
1.(娄底中考)如图,小明用长为3
m的
( http: / / www.21cnjy.com )竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12
m,则旗杆AB的高为________m.21世纪教育网版权所有
2.(北京中考)在某一时刻,测得一根高为1
( http: / / www.21cnjy.com ).8
m的竹竿的影长为3
m,同时测得一根旗杆的影长为25
m,那么这根旗杆的高度为________m.www.21-cn-jy.com
3.已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为________.【来源:21·世纪·教育·网】
4.如图是一束平行的阳光从教室窗户射入的平面示意图,光线与地面所成角∠AMC=30°,在教室地面的影长MN=2米.若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室地面的距离AC为________米.
5.(黔南中考)如图是小明设计用手电来测量都匀
( http: / / www.21cnjy.com )南沙洲古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是________米(平面镜的厚度忽略不计).21·世纪
教育网
知识点2 测量距离
6.(北京中考)如图,为估
( http: / / www.21cnjy.com )算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,EC=10
m,CD=20
m,则河的宽度AB等于( )www-2-1-cnjy-com
A.60
m
B.40
m
C.30
m
D.20
m
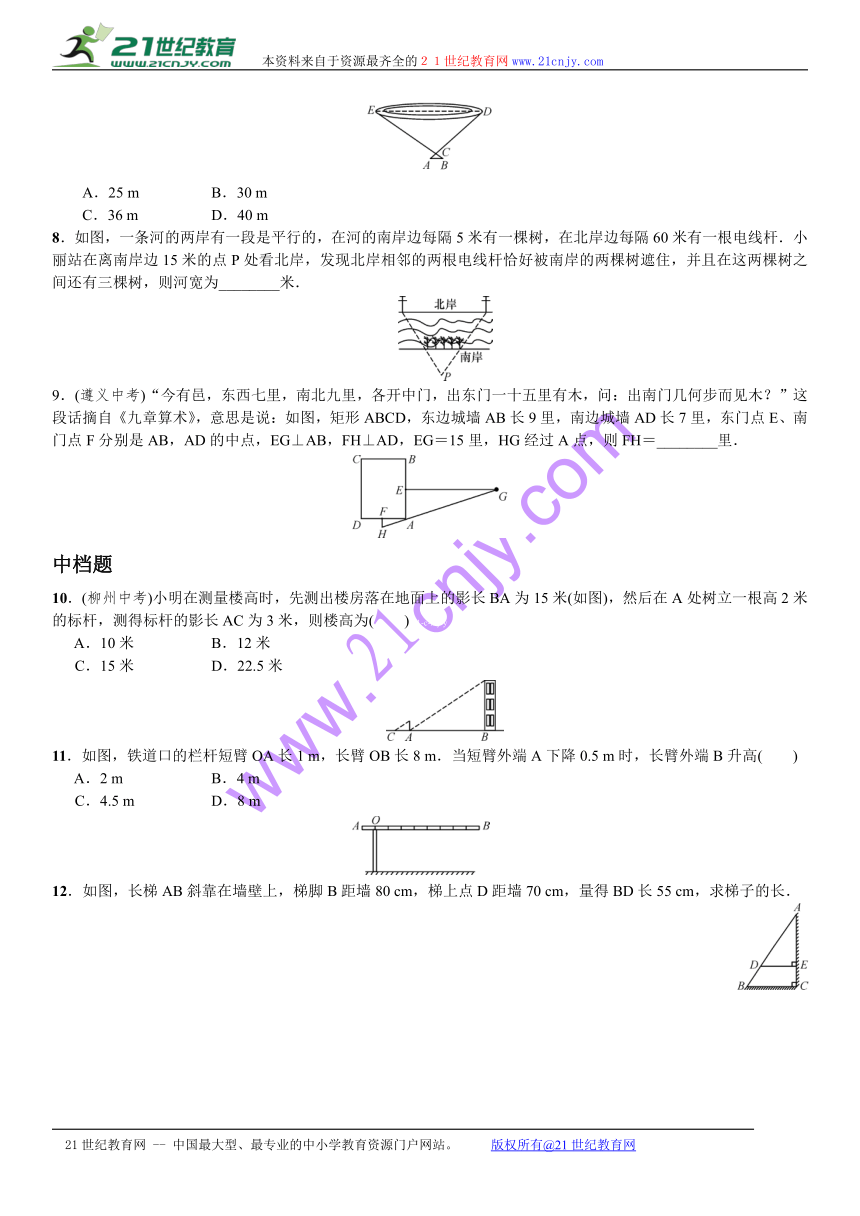
7.如图,为了测量一池塘的宽DE,在岸边找
( http: / / www.21cnjy.com )到一点C,测得CD=30
m,在DC的延长线上找一点A,测得AC=5
m,过点A作AB∥DE交EC的延长线于B,测出AB=6
m,则池塘的宽DE为( )21·cn·jy·com
A.25
m
B.30
m
C.36
m
D.40
m
8.如图,一条河的两岸有一段是平行
( http: / / www.21cnjy.com )的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.21世纪教育网21教育网
9.(遵义中考)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=________里.
中档题
10.(柳州中考)小明在测量楼高时
( http: / / www.21cnjy.com ),先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )2-1-c-n-j-y
A.10米
B.12米
C.15米
D.22.5米
11.如图,铁道口的栏杆短臂OA长1
m,长臂OB长8
m.当短臂外端A下降0.5
m时,长臂外端B升高( )
A.2
m
B.4
m
C.4.5
m
D.8
m
21世纪教育网
12.如图,长梯AB斜靠在墙壁上,梯脚B距墙80
cm,梯上点D距墙70
cm,量得BD长55
cm,求梯子的长.
综合题
13.(绍兴中考)课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120
mm,高AD=80
mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm 21
cnjy
com
小颖解得此题的答案为48
mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此
( http: / / www.21cnjy.com )矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.2·1·c·n·j·y
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.【来源:21cnj
y.co
m】
21世纪教育网
参考答案
1.9 2.15 3.7.5米 4.3 5.8 6.B 7.C 8.30 9.1.05 10.A 11.B 21cnjy.com
12.设梯子的长AB为x
cm.21世纪教育网
∵DE⊥AC,BC⊥AC,
∴Rt△ADE∽Rt△ABC.∴=.∴=.
解得x=440.答:梯子的长是440
cm.
13.(1)设矩形的边长PN=2y
mm,则PQ=y
mm,
由条件可得△APN∽△ABC,∴=,
即=.解得y=.
∴PN=×2=(mm).
答:这个矩形零件的两条边长分别为mm,
mm.
(2)设PN=x
mm,由条件可得△APN∽△ABC,∴=.
即=.
解得PQ=80-x.
∴S=PN·PQ=x(80-x)=-x2+80x=-(x-60)2+2
400.
∴S的最大值为2
400
mm2,此时PN=60
mm,PQ=80-×60=40(mm).
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
27.2.3 相似三角形应用举例
基础题
知识点1 测量物高
1.(娄底中考)如图,小明用长为3
m的
( http: / / www.21cnjy.com )竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12
m,则旗杆AB的高为________m.21世纪教育网版权所有
2.(北京中考)在某一时刻,测得一根高为1
( http: / / www.21cnjy.com ).8
m的竹竿的影长为3
m,同时测得一根旗杆的影长为25
m,那么这根旗杆的高度为________m.www.21-cn-jy.com
3.已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外.将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为________.【来源:21·世纪·教育·网】
4.如图是一束平行的阳光从教室窗户射入的平面示意图,光线与地面所成角∠AMC=30°,在教室地面的影长MN=2米.若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室地面的距离AC为________米.
5.(黔南中考)如图是小明设计用手电来测量都匀
( http: / / www.21cnjy.com )南沙洲古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是________米(平面镜的厚度忽略不计).21·世纪
教育网
知识点2 测量距离
6.(北京中考)如图,为估
( http: / / www.21cnjy.com )算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,EC=10
m,CD=20
m,则河的宽度AB等于( )www-2-1-cnjy-com
A.60
m
B.40
m
C.30
m
D.20
m
7.如图,为了测量一池塘的宽DE,在岸边找
( http: / / www.21cnjy.com )到一点C,测得CD=30
m,在DC的延长线上找一点A,测得AC=5
m,过点A作AB∥DE交EC的延长线于B,测出AB=6
m,则池塘的宽DE为( )21·cn·jy·com
A.25
m
B.30
m
C.36
m
D.40
m
8.如图,一条河的两岸有一段是平行
( http: / / www.21cnjy.com )的,在河的南岸边每隔5米有一棵树,在北岸边每隔60米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.21世纪教育网21教育网
9.(遵义中考)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=________里.
中档题
10.(柳州中考)小明在测量楼高时
( http: / / www.21cnjy.com ),先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )2-1-c-n-j-y
A.10米
B.12米
C.15米
D.22.5米
11.如图,铁道口的栏杆短臂OA长1
m,长臂OB长8
m.当短臂外端A下降0.5
m时,长臂外端B升高( )
A.2
m
B.4
m
C.4.5
m
D.8
m
21世纪教育网
12.如图,长梯AB斜靠在墙壁上,梯脚B距墙80
cm,梯上点D距墙70
cm,量得BD长55
cm,求梯子的长.
综合题
13.(绍兴中考)课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120
mm,高AD=80
mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm 21
cnjy
com
小颖解得此题的答案为48
mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此
( http: / / www.21cnjy.com )矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.2·1·c·n·j·y
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.【来源:21cnj
y.co
m】
21世纪教育网
参考答案
1.9 2.15 3.7.5米 4.3 5.8 6.B 7.C 8.30 9.1.05 10.A 11.B 21cnjy.com
12.设梯子的长AB为x
cm.21世纪教育网
∵DE⊥AC,BC⊥AC,
∴Rt△ADE∽Rt△ABC.∴=.∴=.
解得x=440.答:梯子的长是440
cm.
13.(1)设矩形的边长PN=2y
mm,则PQ=y
mm,
由条件可得△APN∽△ABC,∴=,
即=.解得y=.
∴PN=×2=(mm).
答:这个矩形零件的两条边长分别为mm,
mm.
(2)设PN=x
mm,由条件可得△APN∽△ABC,∴=.
即=.
解得PQ=80-x.
∴S=PN·PQ=x(80-x)=-x2+80x=-(x-60)2+2
400.
∴S的最大值为2
400
mm2,此时PN=60
mm,PQ=80-×60=40(mm).
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
