广西宾阳2016-2017学年高一12月月考数学试题 Word版含答案
文档属性
| 名称 | 广西宾阳2016-2017学年高一12月月考数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 249.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-27 20:23:51 | ||
图片预览


文档简介
宾阳2016年秋学期12月月考高一数学试卷
一、选择题(
每小题5分,12小题共60分
)
1.满足条件的所有集合M的个数是
(
)
A.4
B.3
C
.2
D
.1
2.
函数在区间是增函数,则的递增区间是
(
)
A.
B.
C.
D.
3、已知,则函数的图像必定不经过(
)
A、第一象限
B、第二象限
C、第三象限
D、第四象限
4、是偶函数,且不恒等于零,则(
)
A、是奇函数
B、可能是奇函数,也可能是偶函数
C、是偶函数
D、不是奇函数,也不是偶函数
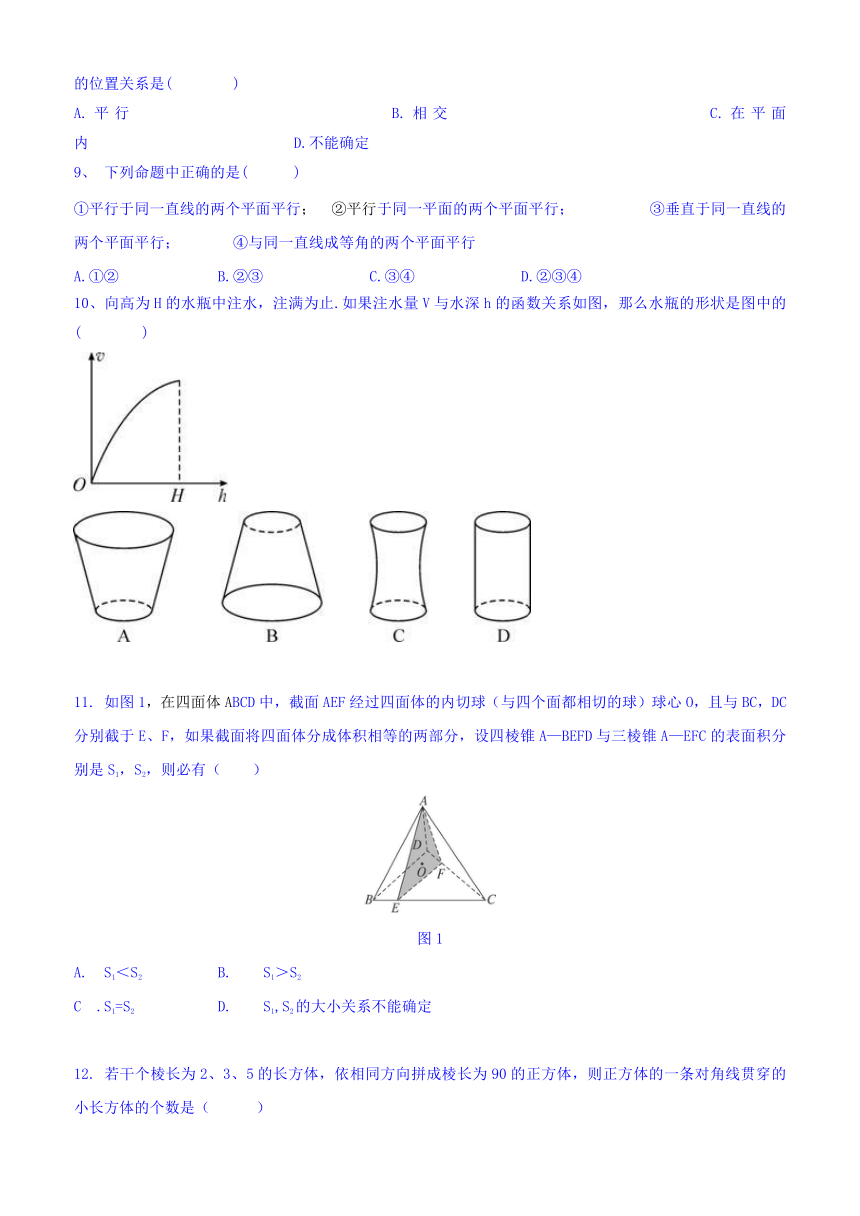
5、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是(
)
6.若函数
f(x)在定义域{x|x∈R
且
x≠0}上是偶函数,且在(0,+
∞
)上是减函数,f(2)=0,则函数
f(x)的零点有(
)
A.1个
B.2个
C.至少
2个
D.无法判断
7、.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为(
)
B.
C.
D.
8.
在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是(
)
A.平行
B.相交
C.在平面内
D.不能确定
9、
下列命题中正确的是(
)
①平行于同一直线的两个平面平行;
②平行于同一平面的两个平面平行;
③垂直于同一直线的两个平面平行;
④与同一直线成等角的两个平面平行
A.①②
B.②③
C.③④
D.②③④
10、向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系如图,那么水瓶的形状是图中的(
)
11.
如图1,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A—BEFD与三棱锥A—EFC的表面积分别是S1,S2,则必有(
)
图1
A.
S1<S2
B.
S1>S2
C
.S1=S2
D.
S1,S2的大小关系不能确定
12.
若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体的一条对角线贯穿的小长方体的个数是(
)
A.64
B.66
C.68
D.以上都错
填空题
(每小题5分共20分)
13
已知函数,则函数的零点是
某企业年产量第二年增长率为r%,第三年增长率为R%,则这两年的平均增长率为 。
15.下列命题中,正确的是
A.如果直l与平面α内无数条直线成异面直线,则l∥α
B.如果直线l与平面α内无数条直线平行,则l∥α
C.如果直线l与平面α内无数条直线成异面直线,则lα
D.如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线
E.如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行
16、三棱柱的底面是边长为1cm
的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达点,则小虫所行的最短路程为
Cm
三、解答题
(共六道大题
合计70分)
17.求下列各式的值:(每小题5分共10分)
(1)
(2)7(
)
-3(
)-6(
)+
18.(
共12分
)已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该三棱锥的侧视图和直观图.(2)求出侧视图的面积.
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )
19.
(本小题12分)、商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/
件,商场以高于成本价的相同价格(标价)出售.
问:(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
20.(
共12分
)
设P、Q是边长为a的正方体AC1的面AA1D1D、面A1B1C1D1的中心,如图,(1)证明PQ∥平面AA1B1B;(2)求C1D1
与直线PQ成的角大小。
21.
(
共12分
)
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
22.(
共12分
)
已知二次函数f(x)=x2-16x+q+3.
(1)若函数在区间上存在零点,求实数q的取值范围;
(2)是否存在常数t(t≥0),当x∈时,f(x)的值域为区间D,且区间D的长度为12-t(视区间的长度为b-a).
高一数学12月月考答案
选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
A
A
B
C
A
B
B
C
B
11.
分析:如图1,连OA、OB、OC、OD,则VA—BEFD=VO—ABD+VO—ABE+VO—BEFD+VO—ADF,VA—EFC=VO—AFC+VO—AEC+VO—EFC,又VA—BEFD=VA—EFC,而每个小三棱锥的高都是原四面体的内切球的半径,故S△ABD+S△ABE+SBEFD+S△ADF=S△AFC+S△AEC+S△EFC,又面AEF是公共面,故选C.
12.
分析:由2、3、5的最小公倍数为30,由2、3、5组成的棱长为30的正方体的一条对角线穿过的长方体为整数个,所以由2、3、5组成棱长为90的正方体的一条对角线穿过的小长方体的个数应为3的倍数.
答案:B
二、填空题
13:
0
、
2
14:
15:
C
16:
5
三
解答题
17、解:。(1)
(2)原式.
18.解
(1)如图.
(7分)
(2)根据三视图间的关系可得BC=2,
侧视图中VA为3==2,∴S△VBC=×2×2=6.(14分)
19:19、解:(Ⅰ)设购买人数为人,羊毛衫的标价为每件元,利润为元,
则
∵,∴时,,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ)由题意得,
所以,商场要获取最大利润的,每件标价为元或元.
:20
(1)
(1)证法一:取AA1,A1B1的中点M,N,连接MN,NQ,MP,
∵MP∥AD,MP=,NQ∥A1D1,NQ=,
∴MP∥ND且MP=ND.∴四边形PQNM为平行四边形.∴PQ∥MN.
∵MN面AA1B1B,PQ面AA1B1B,
∴PQ∥面AA1B1B.
证法二:连接AD1,AB1,在△AB1D1中,显然P,Q分别是AD1,D1B1的中点,
∴PQ∥AB1,且PQ=.
∵PQ面AA1B1B,AB1面AA1B1B,
∴PQ∥面AA1B1B.
∠DC1D1=45度
为所求的PQ与C1D1所成角的度数
:21:解
如图所示,过C作CO1⊥AB于O1,
在半圆中可得∠BCA=90°,
∠BAC=30°,
AB=2R,∴AC=R,BC=R,CO1=R,
∴S球=4πR2,S圆锥AO1侧=π×R×R=πR2,
S圆锥BO1侧=π×R×R=πR2,
∴S几何体表=S球+S圆锥AO1侧+S圆锥BO1侧
=πR2+πR2=πR2,
∴旋转所得到的几何体的表面积为πR2.
又V球=πR3,V圆锥AO1=·AO1·πCO
=πR2·AO1,
V圆锥BO1=BO1·πCO=πR2·BO1,
∴V几何体=V球-(V圆锥AO1+V圆锥BO1)
=πR3-πR3=πR3.
22.解
(1)∵函数f(x)=x2-16x+q+3的对称轴是x=8,∴f(x)在区间上是减函数.
∵函数在区间上存在零点,则必有即∴-20≤q≤12.
(2)∵0≤t<10,f(x)在区间上是减函数,在区间上是增函数,且对称轴是x=8.
①当0≤t≤6时,在区间上,f(t)最大,f(8)最小,
∴f(t)-f(8)=12-t,即t2-15t+52=0,
解得t=,∴t=;
②当6∴f(10)-f(8)=12-t,解得t=8;
③当8∴f(10)-f(t)=12-t,即t2-17t+72=0,解得t=8,9,
∴t=9.
综上可知,存在常数t=,8,9满足条件.
一、选择题(
每小题5分,12小题共60分
)
1.满足条件的所有集合M的个数是
(
)
A.4
B.3
C
.2
D
.1
2.
函数在区间是增函数,则的递增区间是
(
)
A.
B.
C.
D.
3、已知,则函数的图像必定不经过(
)
A、第一象限
B、第二象限
C、第三象限
D、第四象限
4、是偶函数,且不恒等于零,则(
)
A、是奇函数
B、可能是奇函数,也可能是偶函数
C、是偶函数
D、不是奇函数,也不是偶函数
5、如图所示的直观图是将正方体模型放置在你的水平视线的左上角而绘制的,其中正确的是(
)
6.若函数
f(x)在定义域{x|x∈R
且
x≠0}上是偶函数,且在(0,+
∞
)上是减函数,f(2)=0,则函数
f(x)的零点有(
)
A.1个
B.2个
C.至少
2个
D.无法判断
7、.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为(
)
B.
C.
D.
8.
在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是(
)
A.平行
B.相交
C.在平面内
D.不能确定
9、
下列命题中正确的是(
)
①平行于同一直线的两个平面平行;
②平行于同一平面的两个平面平行;
③垂直于同一直线的两个平面平行;
④与同一直线成等角的两个平面平行
A.①②
B.②③
C.③④
D.②③④
10、向高为H的水瓶中注水,注满为止.如果注水量V与水深h的函数关系如图,那么水瓶的形状是图中的(
)
11.
如图1,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A—BEFD与三棱锥A—EFC的表面积分别是S1,S2,则必有(
)
图1
A.
S1<S2
B.
S1>S2
C
.S1=S2
D.
S1,S2的大小关系不能确定
12.
若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体的一条对角线贯穿的小长方体的个数是(
)
A.64
B.66
C.68
D.以上都错
填空题
(每小题5分共20分)
13
已知函数,则函数的零点是
某企业年产量第二年增长率为r%,第三年增长率为R%,则这两年的平均增长率为 。
15.下列命题中,正确的是
A.如果直l与平面α内无数条直线成异面直线,则l∥α
B.如果直线l与平面α内无数条直线平行,则l∥α
C.如果直线l与平面α内无数条直线成异面直线,则lα
D.如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线
E.如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行
16、三棱柱的底面是边长为1cm
的正三角形,侧面是长方形,侧棱长为4cm,一个小虫从A点出发沿表面一圈到达点,则小虫所行的最短路程为
Cm
三、解答题
(共六道大题
合计70分)
17.求下列各式的值:(每小题5分共10分)
(1)
(2)7(
)
-3(
)-6(
)+
18.(
共12分
)已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该三棱锥的侧视图和直观图.(2)求出侧视图的面积.
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )
19.
(本小题12分)、商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/
件,商场以高于成本价的相同价格(标价)出售.
问:(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
20.(
共12分
)
设P、Q是边长为a的正方体AC1的面AA1D1D、面A1B1C1D1的中心,如图,(1)证明PQ∥平面AA1B1B;(2)求C1D1
与直线PQ成的角大小。
21.
(
共12分
)
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
22.(
共12分
)
已知二次函数f(x)=x2-16x+q+3.
(1)若函数在区间上存在零点,求实数q的取值范围;
(2)是否存在常数t(t≥0),当x∈时,f(x)的值域为区间D,且区间D的长度为12-t(视区间的长度为b-a).
高一数学12月月考答案
选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
A
A
B
C
A
B
B
C
B
11.
分析:如图1,连OA、OB、OC、OD,则VA—BEFD=VO—ABD+VO—ABE+VO—BEFD+VO—ADF,VA—EFC=VO—AFC+VO—AEC+VO—EFC,又VA—BEFD=VA—EFC,而每个小三棱锥的高都是原四面体的内切球的半径,故S△ABD+S△ABE+SBEFD+S△ADF=S△AFC+S△AEC+S△EFC,又面AEF是公共面,故选C.
12.
分析:由2、3、5的最小公倍数为30,由2、3、5组成的棱长为30的正方体的一条对角线穿过的长方体为整数个,所以由2、3、5组成棱长为90的正方体的一条对角线穿过的小长方体的个数应为3的倍数.
答案:B
二、填空题
13:
0
、
2
14:
15:
C
16:
5
三
解答题
17、解:。(1)
(2)原式.
18.解
(1)如图.
(7分)
(2)根据三视图间的关系可得BC=2,
侧视图中VA为3==2,∴S△VBC=×2×2=6.(14分)
19:19、解:(Ⅰ)设购买人数为人,羊毛衫的标价为每件元,利润为元,
则
∵,∴时,,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ)由题意得,
所以,商场要获取最大利润的,每件标价为元或元.
:20
(1)
(1)证法一:取AA1,A1B1的中点M,N,连接MN,NQ,MP,
∵MP∥AD,MP=,NQ∥A1D1,NQ=,
∴MP∥ND且MP=ND.∴四边形PQNM为平行四边形.∴PQ∥MN.
∵MN面AA1B1B,PQ面AA1B1B,
∴PQ∥面AA1B1B.
证法二:连接AD1,AB1,在△AB1D1中,显然P,Q分别是AD1,D1B1的中点,
∴PQ∥AB1,且PQ=.
∵PQ面AA1B1B,AB1面AA1B1B,
∴PQ∥面AA1B1B.
∠DC1D1=45度
为所求的PQ与C1D1所成角的度数
:21:解
如图所示,过C作CO1⊥AB于O1,
在半圆中可得∠BCA=90°,
∠BAC=30°,
AB=2R,∴AC=R,BC=R,CO1=R,
∴S球=4πR2,S圆锥AO1侧=π×R×R=πR2,
S圆锥BO1侧=π×R×R=πR2,
∴S几何体表=S球+S圆锥AO1侧+S圆锥BO1侧
=πR2+πR2=πR2,
∴旋转所得到的几何体的表面积为πR2.
又V球=πR3,V圆锥AO1=·AO1·πCO
=πR2·AO1,
V圆锥BO1=BO1·πCO=πR2·BO1,
∴V几何体=V球-(V圆锥AO1+V圆锥BO1)
=πR3-πR3=πR3.
22.解
(1)∵函数f(x)=x2-16x+q+3的对称轴是x=8,∴f(x)在区间上是减函数.
∵函数在区间上存在零点,则必有即∴-20≤q≤12.
(2)∵0≤t<10,f(x)在区间上是减函数,在区间上是增函数,且对称轴是x=8.
①当0≤t≤6时,在区间上,f(t)最大,f(8)最小,
∴f(t)-f(8)=12-t,即t2-15t+52=0,
解得t=,∴t=;
②当6
③当8
∴t=9.
综上可知,存在常数t=,8,9满足条件.
同课章节目录
