28.2.2与方向角、坡角有关的解直角三角形应用题(第2课时)课文练习含答案
文档属性
| 名称 | 28.2.2与方向角、坡角有关的解直角三角形应用题(第2课时)课文练习含答案 | 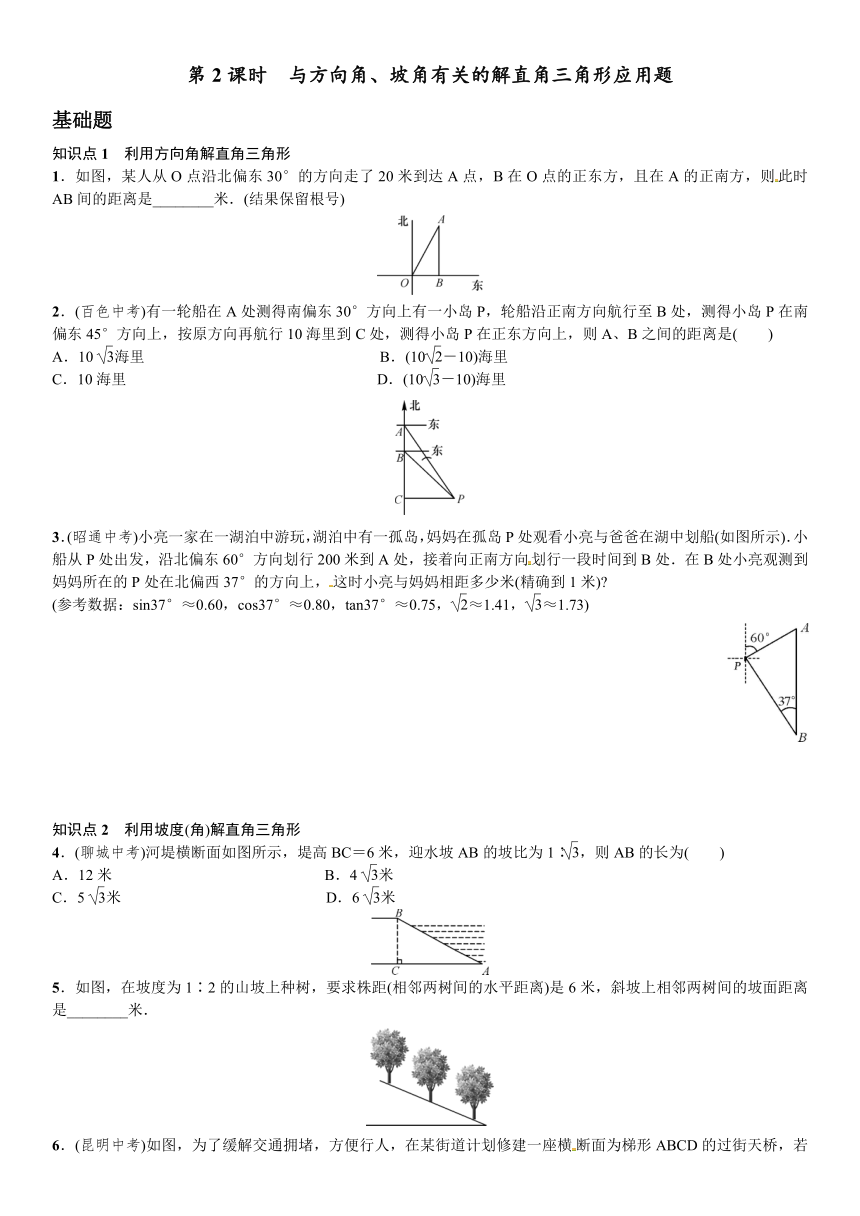 | |
| 格式 | zip | ||
| 文件大小 | 160.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 07:57:10 | ||
图片预览


文档简介
第2课时 与方向角、坡角有关的解直角三角形应用题
基础题
知识点1 利用方向角解直角三角形
1.如图,某人从O点沿北偏东30°的方向走了20米到达A点,B在O点的正东方,且在A的正南方,则此时AB间的距离是________米.(结果保留根号)
2.(百色中考)有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里到C处,测得小岛P在正东方向上,则A、B之间的距离是( )
A.10海里
B.(10-10)海里
C.10海里
D.(10-10)海里
3.(昭通中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
知识点2 利用坡度(角)解直角三角形
4.(聊城中考)河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶,则AB的长为( )
A.12米
B.4米
C.5米
D.6米
5.如图,在坡度为1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是________米.
6.(昆明中考)如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1∶1.2(垂直高度CE与水平宽度DE的比),上底BC=10
m,天桥高度CE=5
m,求天桥下底AD的长度.(结果精确到0.1
m,参考数据:sin35°≈
0.57,cos35°≈
0.82,tan35°≈
0.70)
中档题
7.(铜仁中考)如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.已知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(≈1.732)
8.(遵义中考)如图,一楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
综合题
9.(南充中考)马航MH370失联后,我国政府积极参与搜救.某日,我国两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,如图,可疑漂浮物P在救助船A的北偏东53.5°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
参考答案
1.10 2.D
3.过P作PC⊥AB于C,
在Rt△APC中,AP
=
200
m,∠ACP
=
90°,∠PAC
=
60°.
∴PC=
200×sin60°=200
×=100(m).
∵在Rt△PBC中,sin37°=,∴PB==≈288(m).
答:小亮与妈妈相距约288米.
4.A 5.3
6.过B点作BF⊥AD于点F.
∵四边形BFEC是矩形,∴BF=CE=5
m,EF=BC=10
m.
∵在Rt△ABF中,∠BAF=35°,tan∠BAF=,
∴AF=≈≈7.14(m).
∵斜坡CD的坡度为i=1∶1.2,∴=,ED=1.2CE=1.2×5=6(m).
∴AD=AF+FE+ED=7.14+10+6=23.14≈23.1(m).
答:天桥下底AD的长度为23.1
m.
7.该轮船不改变航向继续前行,没有触礁危险.
理由如下:由题意,得∠ABD=30°,∠ACD=60°.
∴∠CAB=∠ABD,∴BC=AC=200海里.
在Rt△ACD中,设CD=x海里,则AC=2x,AD===x.
在Rt△ABD中,AB=2AD=2x,BD===3x.
又∵BD=BC+CD,∴3x=200+x,解得x=100.
∴AD=x=100≈173.2,
∵173.2海里>170海里,∴轮船不改变航向继续向前行驶,轮船无触礁的危险.
8.过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,∵i===tan∠ECF,∴∠ECF=30°.
∴EF=CE=10米,CF=10米.
∴BH=EF=10米,HE=BF=BC+CF=(25+10)米.
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10)米.
∴AB=AH+HB=(35+10)米.
答:楼房AB的高为(35+10)米.
9.(1)过点P作PH⊥AB于点H,
根据题意,得∠PAH=90°-53.5°=36.5°,∠PBH=45°,AB=140海里.
设PH=x海里,在Rt△PHB中,tan45°=,
∴BH=x.在Rt△PHA中,tan36.5°=,∴AH==x.
又∵AB=140,∴x+x=140,解得x=60,即PH=60.
答:可疑漂浮物P到A、B两船所在直线的距离为60海里.
(2)在Rt△PHA中,AH=×60=80,PA==100.
救助船A到达P处的时间tA=100÷40=2.5(小时);
在Rt△PHB中,PB==60,
救助船B到达P处的时间tB=60÷30=2(小时).
∵2.5<2,∴救助船A先到达P处.
基础题
知识点1 利用方向角解直角三角形
1.如图,某人从O点沿北偏东30°的方向走了20米到达A点,B在O点的正东方,且在A的正南方,则此时AB间的距离是________米.(结果保留根号)
2.(百色中考)有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里到C处,测得小岛P在正东方向上,则A、B之间的距离是( )
A.10海里
B.(10-10)海里
C.10海里
D.(10-10)海里
3.(昭通中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈1.73)
知识点2 利用坡度(角)解直角三角形
4.(聊城中考)河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1∶,则AB的长为( )
A.12米
B.4米
C.5米
D.6米
5.如图,在坡度为1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是________米.
6.(昆明中考)如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1∶1.2(垂直高度CE与水平宽度DE的比),上底BC=10
m,天桥高度CE=5
m,求天桥下底AD的长度.(结果精确到0.1
m,参考数据:sin35°≈
0.57,cos35°≈
0.82,tan35°≈
0.70)
中档题
7.(铜仁中考)如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.已知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(≈1.732)
8.(遵义中考)如图,一楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
综合题
9.(南充中考)马航MH370失联后,我国政府积极参与搜救.某日,我国两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,如图,可疑漂浮物P在救助船A的北偏东53.5°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75)
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
参考答案
1.10 2.D
3.过P作PC⊥AB于C,
在Rt△APC中,AP
=
200
m,∠ACP
=
90°,∠PAC
=
60°.
∴PC=
200×sin60°=200
×=100(m).
∵在Rt△PBC中,sin37°=,∴PB==≈288(m).
答:小亮与妈妈相距约288米.
4.A 5.3
6.过B点作BF⊥AD于点F.
∵四边形BFEC是矩形,∴BF=CE=5
m,EF=BC=10
m.
∵在Rt△ABF中,∠BAF=35°,tan∠BAF=,
∴AF=≈≈7.14(m).
∵斜坡CD的坡度为i=1∶1.2,∴=,ED=1.2CE=1.2×5=6(m).
∴AD=AF+FE+ED=7.14+10+6=23.14≈23.1(m).
答:天桥下底AD的长度为23.1
m.
7.该轮船不改变航向继续前行,没有触礁危险.
理由如下:由题意,得∠ABD=30°,∠ACD=60°.
∴∠CAB=∠ABD,∴BC=AC=200海里.
在Rt△ACD中,设CD=x海里,则AC=2x,AD===x.
在Rt△ABD中,AB=2AD=2x,BD===3x.
又∵BD=BC+CD,∴3x=200+x,解得x=100.
∴AD=x=100≈173.2,
∵173.2海里>170海里,∴轮船不改变航向继续向前行驶,轮船无触礁的危险.
8.过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,∵i===tan∠ECF,∴∠ECF=30°.
∴EF=CE=10米,CF=10米.
∴BH=EF=10米,HE=BF=BC+CF=(25+10)米.
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10)米.
∴AB=AH+HB=(35+10)米.
答:楼房AB的高为(35+10)米.
9.(1)过点P作PH⊥AB于点H,
根据题意,得∠PAH=90°-53.5°=36.5°,∠PBH=45°,AB=140海里.
设PH=x海里,在Rt△PHB中,tan45°=,
∴BH=x.在Rt△PHA中,tan36.5°=,∴AH==x.
又∵AB=140,∴x+x=140,解得x=60,即PH=60.
答:可疑漂浮物P到A、B两船所在直线的距离为60海里.
(2)在Rt△PHA中,AH=×60=80,PA==100.
救助船A到达P处的时间tA=100÷40=2.5(小时);
在Rt△PHB中,PB==60,
救助船B到达P处的时间tB=60÷30=2(小时).
∵2.5<2,∴救助船A先到达P处.
