3.3 二倍角的三角函数 同步练习4(含答案)
文档属性
| 名称 | 3.3 二倍角的三角函数 同步练习4(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 16:36:40 | ||
图片预览
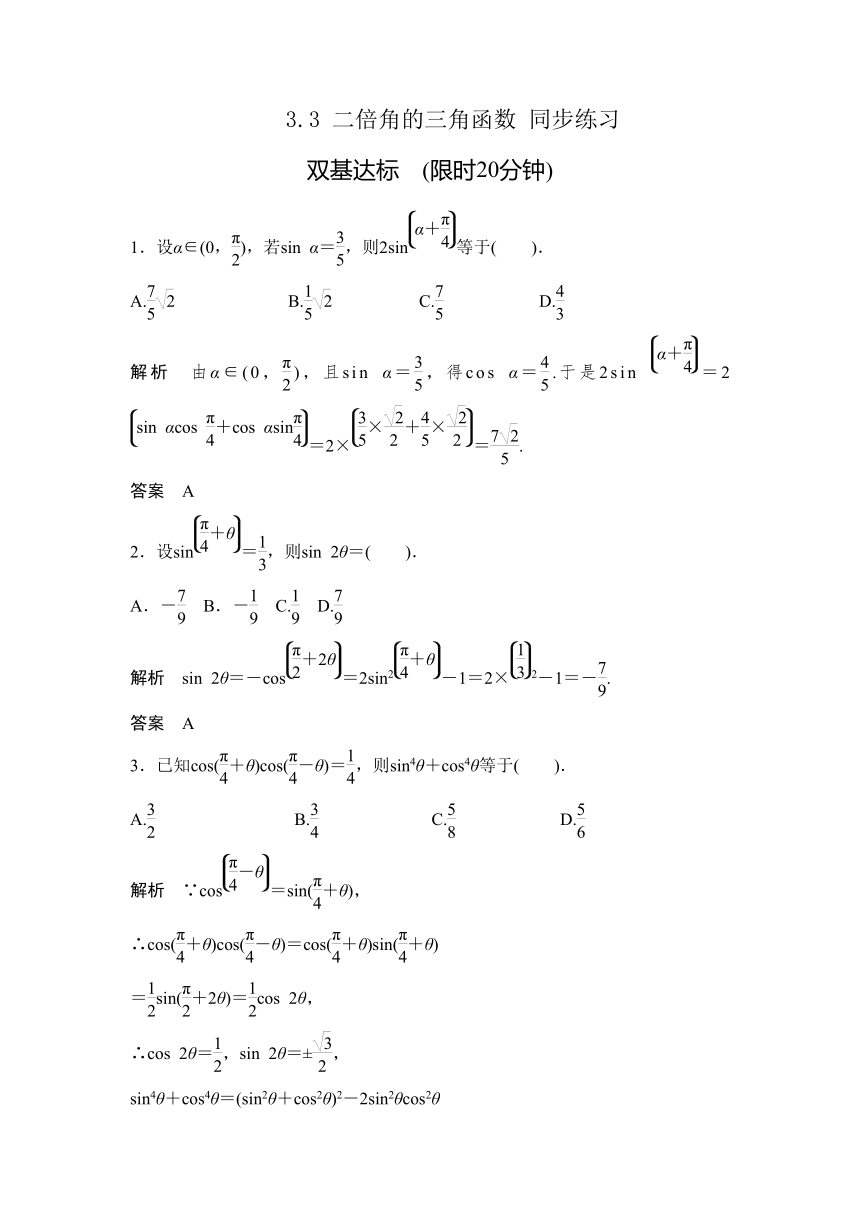
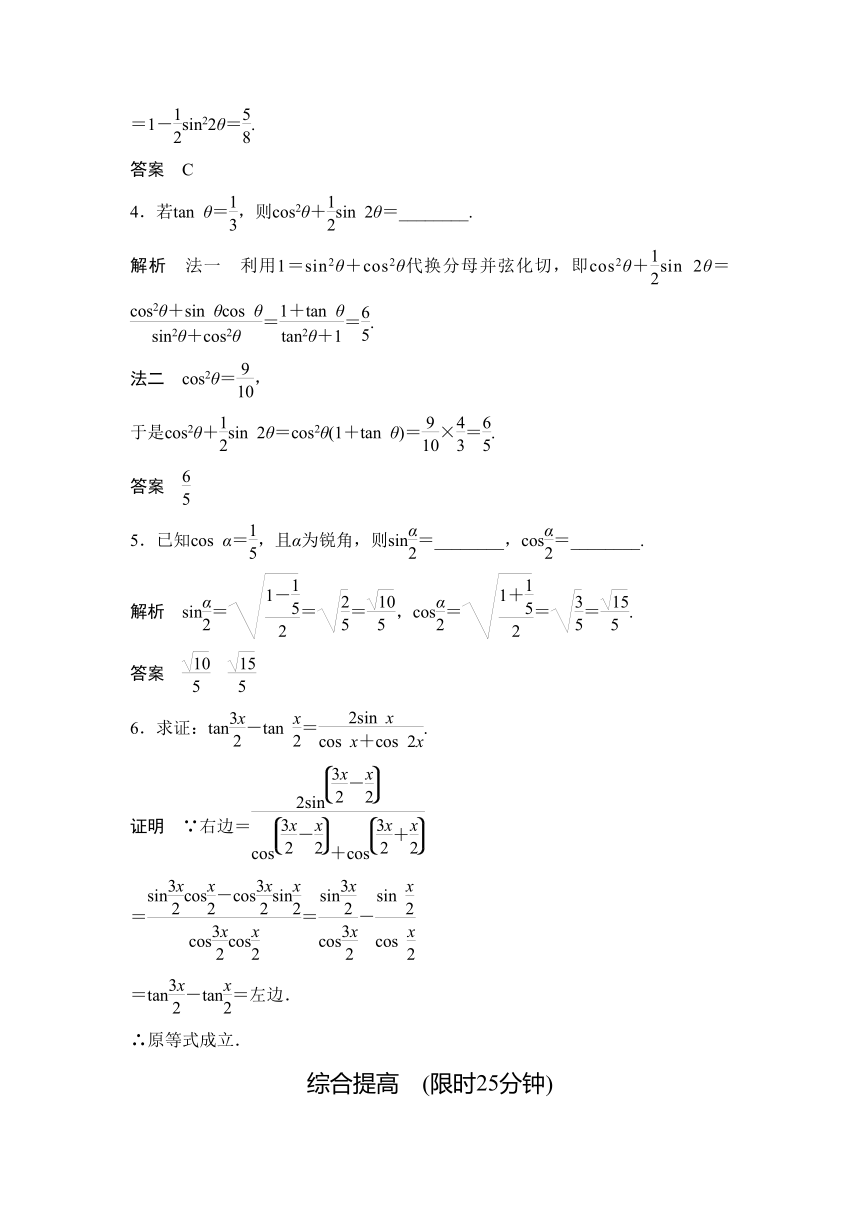

文档简介
3.3
二倍角的三角函数
同步练习
双基达标 限时20分钟
1.设α∈(0,),若sin
α=,则2sin等于( ).
A.
B.
C.
D.
解析 由α∈(0,),且sin
α=,得cos
α=.于是2sin
=2=2×=.
答案 A
2.设sin=,则sin
2θ=( ).
A.-
B.-
C.
D.
解析 sin
2θ=-cos=2sin2-1=2×2-1=-.
答案 A
3.已知cos(+θ)cos(-θ)=,则sin4θ+cos4θ等于( ).
A.
B.
C.
D.
解析 ∵cos=sin(+θ),
∴cos(+θ)cos(-θ)=cos(+θ)sin(+θ)
=sin(+2θ)=cos
2θ,
∴cos
2θ=,sin
2θ=±,
sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-sin22θ=.
答案 C
4.若tan
θ=,则cos2θ+sin
2θ=________.
解析 法一 利用1=sin2θ+cos2θ代换分母并弦化切,即cos2θ+sin
2θ===.
法二 cos2θ=,
于是cos2θ+sin
2θ=cos2θ(1+tan
θ)=×=.
答案
5.已知cos
α=,且α为锐角,则sin=________,cos=________.
解析 sin===,cos===.
答案
6.求证:tan-tan
=.
证明 ∵右边=
==-
=tan-tan=左边.
∴原等式成立.
综合提高 限时25分钟
7.若函数f(x+2)=则f·f(-98)等于( ).
A.
B.-
C.2
D.-2
解析 ∵f(x+2)=
∴f(x)=
则f(+2)·f(-98)=tan×lg
100=1×2=2.
答案 C
8.已知方程x2+4ax+3a+1=0(a>1)的两根为tan
α、tan
β,且α、β∈,
则tan的值是( ).
A.
B.-2
C.
D.或-2
解析 ∵ =.
∴tan(α+β)=.
∵则-π<α+β<0,-<<0.
∴tan(α+β)== tan=-2或tan=(舍去).
答案 B
9.已知tan=2,
则的值为________.
解析 ∵tan==2,
∴tan
x=.
又∵tan
2x=,
∴=(1-tan2
x)==.
答案
10.已知sin
α=+cos
α,且α∈,则的值为________.
解析 ∵sin2
α+cos2α=1,sin
α=+cos
α,
∴2+cos2
α=1.
∴2cos2α+cos
α-=0.
∴cos
α=.
∵α∈,∴cos
α>0.
∴cos
α=.∴sin
α=+cos
α=.
∴==-(sin
α+cos
α)
=-
=-.
答案 -
11.(1)f(α)=2tan
α-,求f;
(2)已知tan
2θ=-2,π<2θ<2π,求的值.
解 (1)f(α)=2tan
α-=+=,
∴f()==8.
(2)原式==,
又tan
2θ==-2,解得tan
θ=-或tan
θ=.
∵π<2θ<2π,∴<θ<π,
∴tan
θ=-,故原式==3+2.
12.(创新拓展)已知函数f(x)=2cos2ωx+2sin
ωxcos
ωx+1(x∈R,ω>0)的最小正周期是.
(1)求ω的值;
(2)求函数f(x)的最大值,并且求使f(x)取得最大值的x的集合.
解 (1)f(x)=2·+sin
2ωx+1
=sin
2ωx+cos
2ωx+2
=+2
=sin+2.
由题设,函数f(x)的最小正周期是,可得=,
所以ω=2.
(2)由(1)知,f(x)=sin+2.
当4x+=+2kπ,即x=+(k∈Z)时,sin取得最大值1,
所以函数f(x)的最大值是2+,此时x的集合为.
二倍角的三角函数
同步练习
双基达标 限时20分钟
1.设α∈(0,),若sin
α=,则2sin等于( ).
A.
B.
C.
D.
解析 由α∈(0,),且sin
α=,得cos
α=.于是2sin
=2=2×=.
答案 A
2.设sin=,则sin
2θ=( ).
A.-
B.-
C.
D.
解析 sin
2θ=-cos=2sin2-1=2×2-1=-.
答案 A
3.已知cos(+θ)cos(-θ)=,则sin4θ+cos4θ等于( ).
A.
B.
C.
D.
解析 ∵cos=sin(+θ),
∴cos(+θ)cos(-θ)=cos(+θ)sin(+θ)
=sin(+2θ)=cos
2θ,
∴cos
2θ=,sin
2θ=±,
sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ
=1-sin22θ=.
答案 C
4.若tan
θ=,则cos2θ+sin
2θ=________.
解析 法一 利用1=sin2θ+cos2θ代换分母并弦化切,即cos2θ+sin
2θ===.
法二 cos2θ=,
于是cos2θ+sin
2θ=cos2θ(1+tan
θ)=×=.
答案
5.已知cos
α=,且α为锐角,则sin=________,cos=________.
解析 sin===,cos===.
答案
6.求证:tan-tan
=.
证明 ∵右边=
==-
=tan-tan=左边.
∴原等式成立.
综合提高 限时25分钟
7.若函数f(x+2)=则f·f(-98)等于( ).
A.
B.-
C.2
D.-2
解析 ∵f(x+2)=
∴f(x)=
则f(+2)·f(-98)=tan×lg
100=1×2=2.
答案 C
8.已知方程x2+4ax+3a+1=0(a>1)的两根为tan
α、tan
β,且α、β∈,
则tan的值是( ).
A.
B.-2
C.
D.或-2
解析 ∵ =.
∴tan(α+β)=.
∵则-π<α+β<0,-<<0.
∴tan(α+β)== tan=-2或tan=(舍去).
答案 B
9.已知tan=2,
则的值为________.
解析 ∵tan==2,
∴tan
x=.
又∵tan
2x=,
∴=(1-tan2
x)==.
答案
10.已知sin
α=+cos
α,且α∈,则的值为________.
解析 ∵sin2
α+cos2α=1,sin
α=+cos
α,
∴2+cos2
α=1.
∴2cos2α+cos
α-=0.
∴cos
α=.
∵α∈,∴cos
α>0.
∴cos
α=.∴sin
α=+cos
α=.
∴==-(sin
α+cos
α)
=-
=-.
答案 -
11.(1)f(α)=2tan
α-,求f;
(2)已知tan
2θ=-2,π<2θ<2π,求的值.
解 (1)f(α)=2tan
α-=+=,
∴f()==8.
(2)原式==,
又tan
2θ==-2,解得tan
θ=-或tan
θ=.
∵π<2θ<2π,∴<θ<π,
∴tan
θ=-,故原式==3+2.
12.(创新拓展)已知函数f(x)=2cos2ωx+2sin
ωxcos
ωx+1(x∈R,ω>0)的最小正周期是.
(1)求ω的值;
(2)求函数f(x)的最大值,并且求使f(x)取得最大值的x的集合.
解 (1)f(x)=2·+sin
2ωx+1
=sin
2ωx+cos
2ωx+2
=+2
=sin+2.
由题设,函数f(x)的最小正周期是,可得=,
所以ω=2.
(2)由(1)知,f(x)=sin+2.
当4x+=+2kπ,即x=+(k∈Z)时,sin取得最大值1,
所以函数f(x)的最大值是2+,此时x的集合为.
