3.3 二倍角的三角函数 同步练习7(含答案)
文档属性
| 名称 | 3.3 二倍角的三角函数 同步练习7(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 125.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 15:30:32 | ||
图片预览


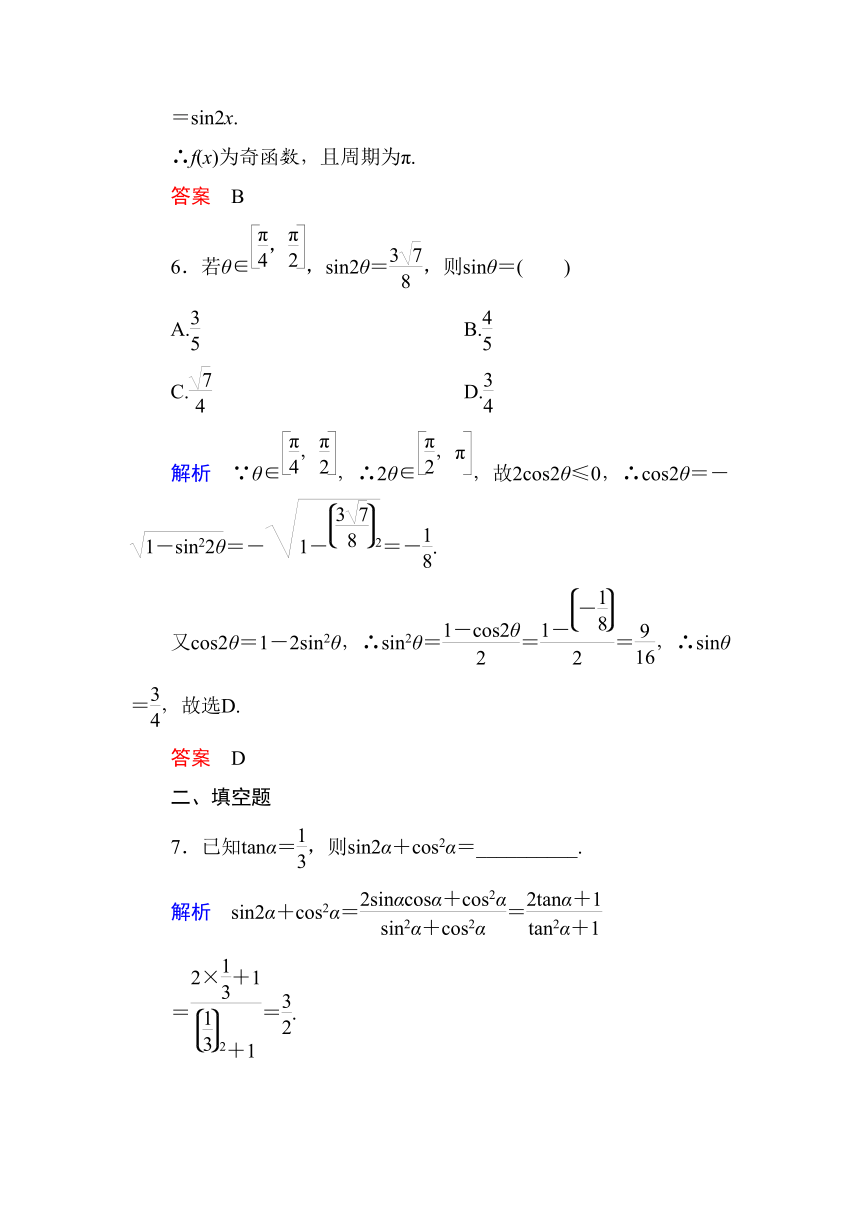
文档简介
3.3
二倍角的三角函数
同步练习
一、选择题
1.cos2-的值为( )
A.1
B.
C.
D.
解析 cos2-===.
答案 D
2.-=( )
A.-2sin5°
B.2sin5°
C.-2cos5°
D.2cos5°
解析 原式=-=|cos5°-sin5°|-|cos5°+sin5°|=-2sin5°.
答案 A
3.若tanθ+=4,则sin2θ=( )
A.
B.
C.
D.
解析 方法一:∵tanθ+==4,
∴4tanθ=1+tan2θ,
∴sin2θ=2sinθcosθ====.
方法二:∵tanθ+=+==.
∴4=,故sin2θ=.
答案 D
4.已知向量a=(2,sinx),b=(cos2x,2cosx),则函数f(x)=a·b的最小正周期是( )
A.
B.π
C.2π
D.4π
解析 ∵f(x)=a·b=2cos2x+2sinxcosx
=1+cos2x+sin2x
=1+sin,
∴f(x)=a·b的最小正周期是π.
答案 B
5.函数f(x)=sin2-sin2是( )
A.周期为π的偶函数
B.周期为π的奇函数
C.周期为2π的偶函数
D.周期为2π的奇函数
解析 f(x)=sin2-sin2
=cos2-sin2
=cos2-sin2
=cos
=sin2x.
∴f(x)为奇函数,且周期为π.
答案 B
6.若θ∈,sin2θ=,则sinθ=( )
A.
B.
C.
D.
解析 ∵θ∈,∴2θ∈,故2cos2θ≤0,∴cos2θ=-=-=-.
又cos2θ=1-2sin2θ,∴sin2θ===,∴sinθ=,故选D.
答案 D
二、填空题
7.已知tanα=,则sin2α+cos2α=__________.
解析 sin2α+cos2α==
==.
答案
8.若f(sinx)=3-cos2x,则f(cosx)=__________.
解析 f(sinx)=3-cos2x=3-(1-2sin2x)=2+2sin2x,f(cosx)=2+2cos2x=2+1+cos2x=3+cos2x.
答案 3+cos2x
9.若sin=-,0≤α≤π,则tanα的值是________.
解析 两边平方得sin2=2-2,
∴=2-2|cosα|.①
当0≤α≤时,①式为=2-2cosα,
∴cosα=1,∴α=0,∴tanα=0.
当<α≤π时,①式为=2+2cosα,
∴cosα=-,∴sinα=.
∴tanα=-
答案 0或-
三、解答题
10.已知cosθ=-,并且180°<θ<270°,求tan.
解 解法一:因为180°<θ<270°,所以90°<<135°,即是第二象限角,所以tan<0,
∴tan=-=-=-2.
解法二:因为180°<θ<270°,即θ是第三象限角,
∴sinθ=-=-=-,
∴tan===-2,
或tan===-2.
11.化简:
(180°<α<360°).
解 原式
=
∵180°<α<360°,∴90°<<180°,故cos<0,
∴上式=
=cos2-sin2=cosα.
12.已知函数f(x)=2acos2x+bsinxcosx-,且f(0)=,f=,
(1)求f(x)的解析式;
(2)写出f(x)的单调增区间.
解 (1)由题意得得
∴f(x)=cos2x+sinxcosx-
=·+sin2x-
=cos2x+sin2x=sin.
(2)由2kπ-≤2x+≤2kπ+(k∈Z),
得-π+kπ≤x≤kπ+(k∈Z).
∴f(x)的单调增区间为(k∈Z).
13.已知向量a=(1+sin2x,sinx-cosx),b=(1,sinx+cosx),函数f(x)=a·b.
(1)求f(x)的最大值及相应的x值;
(2)若f(θ)=,求cos2的值.
解 (1)因为a=(1+sin2x,sinx-cosx),
b=(1,sinx+cosx),
所以f(x)=1+sin2x+sin2x-cos2x=1+sin2x-cos2x=sin(2x-)+1.
因此,当2x-=2kπ+,即x=kπ+(k∈Z)时,f(x)取得最大值+1.
(2)由f(θ)=1+sin2θ-cos2θ及f(θ)=得sin2θ-cos2θ=,两边平方得1-sin4θ=,
即sin4θ=.
因此,cos2(-2θ)=cos(-4θ)=sin4θ=.
二倍角的三角函数
同步练习
一、选择题
1.cos2-的值为( )
A.1
B.
C.
D.
解析 cos2-===.
答案 D
2.-=( )
A.-2sin5°
B.2sin5°
C.-2cos5°
D.2cos5°
解析 原式=-=|cos5°-sin5°|-|cos5°+sin5°|=-2sin5°.
答案 A
3.若tanθ+=4,则sin2θ=( )
A.
B.
C.
D.
解析 方法一:∵tanθ+==4,
∴4tanθ=1+tan2θ,
∴sin2θ=2sinθcosθ====.
方法二:∵tanθ+=+==.
∴4=,故sin2θ=.
答案 D
4.已知向量a=(2,sinx),b=(cos2x,2cosx),则函数f(x)=a·b的最小正周期是( )
A.
B.π
C.2π
D.4π
解析 ∵f(x)=a·b=2cos2x+2sinxcosx
=1+cos2x+sin2x
=1+sin,
∴f(x)=a·b的最小正周期是π.
答案 B
5.函数f(x)=sin2-sin2是( )
A.周期为π的偶函数
B.周期为π的奇函数
C.周期为2π的偶函数
D.周期为2π的奇函数
解析 f(x)=sin2-sin2
=cos2-sin2
=cos2-sin2
=cos
=sin2x.
∴f(x)为奇函数,且周期为π.
答案 B
6.若θ∈,sin2θ=,则sinθ=( )
A.
B.
C.
D.
解析 ∵θ∈,∴2θ∈,故2cos2θ≤0,∴cos2θ=-=-=-.
又cos2θ=1-2sin2θ,∴sin2θ===,∴sinθ=,故选D.
答案 D
二、填空题
7.已知tanα=,则sin2α+cos2α=__________.
解析 sin2α+cos2α==
==.
答案
8.若f(sinx)=3-cos2x,则f(cosx)=__________.
解析 f(sinx)=3-cos2x=3-(1-2sin2x)=2+2sin2x,f(cosx)=2+2cos2x=2+1+cos2x=3+cos2x.
答案 3+cos2x
9.若sin=-,0≤α≤π,则tanα的值是________.
解析 两边平方得sin2=2-2,
∴=2-2|cosα|.①
当0≤α≤时,①式为=2-2cosα,
∴cosα=1,∴α=0,∴tanα=0.
当<α≤π时,①式为=2+2cosα,
∴cosα=-,∴sinα=.
∴tanα=-
答案 0或-
三、解答题
10.已知cosθ=-,并且180°<θ<270°,求tan.
解 解法一:因为180°<θ<270°,所以90°<<135°,即是第二象限角,所以tan<0,
∴tan=-=-=-2.
解法二:因为180°<θ<270°,即θ是第三象限角,
∴sinθ=-=-=-,
∴tan===-2,
或tan===-2.
11.化简:
(180°<α<360°).
解 原式
=
∵180°<α<360°,∴90°<<180°,故cos<0,
∴上式=
=cos2-sin2=cosα.
12.已知函数f(x)=2acos2x+bsinxcosx-,且f(0)=,f=,
(1)求f(x)的解析式;
(2)写出f(x)的单调增区间.
解 (1)由题意得得
∴f(x)=cos2x+sinxcosx-
=·+sin2x-
=cos2x+sin2x=sin.
(2)由2kπ-≤2x+≤2kπ+(k∈Z),
得-π+kπ≤x≤kπ+(k∈Z).
∴f(x)的单调增区间为(k∈Z).
13.已知向量a=(1+sin2x,sinx-cosx),b=(1,sinx+cosx),函数f(x)=a·b.
(1)求f(x)的最大值及相应的x值;
(2)若f(θ)=,求cos2的值.
解 (1)因为a=(1+sin2x,sinx-cosx),
b=(1,sinx+cosx),
所以f(x)=1+sin2x+sin2x-cos2x=1+sin2x-cos2x=sin(2x-)+1.
因此,当2x-=2kπ+,即x=kπ+(k∈Z)时,f(x)取得最大值+1.
(2)由f(θ)=1+sin2θ-cos2θ及f(θ)=得sin2θ-cos2θ=,两边平方得1-sin4θ=,
即sin4θ=.
因此,cos2(-2θ)=cos(-4θ)=sin4θ=.
