1.4.3 单位圆与诱导公式 同步练习3(含答案)
文档属性
| 名称 | 1.4.3 单位圆与诱导公式 同步练习3(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 123.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 00:00:00 | ||
图片预览
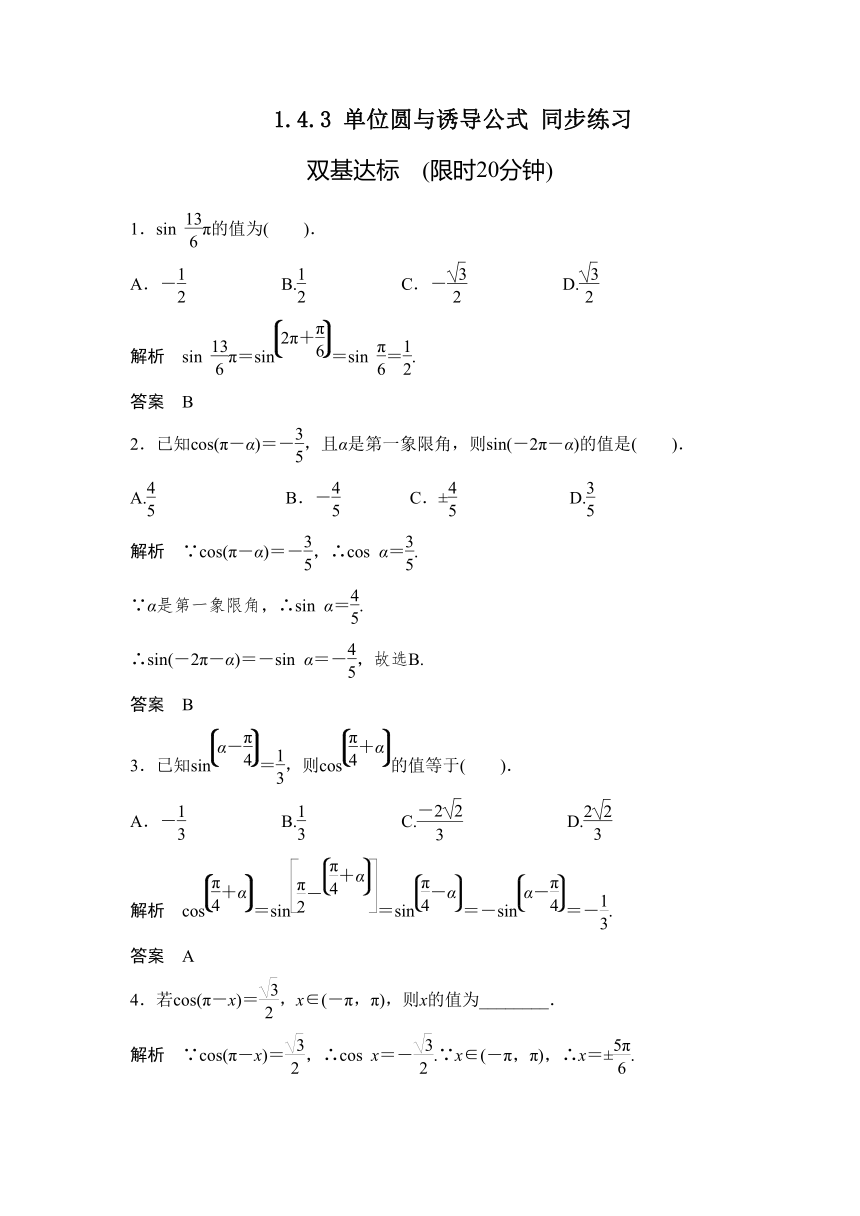

文档简介
1.4.3
单位圆与诱导公式
同步练习
双基达标 限时20分钟
1.sin
π的值为( ).
A.-
B.
C.-
D.
解析 sin
π=sin=sin
=.
答案 B
2.已知cos(π-α)=-,且α是第一象限角,则sin(-2π-α)的值是( ).
A.
B.-
C.±
D.
解析 ∵cos(π-α)=-,∴cos
α=.
∵α是第一象限角,∴sin
α=.
∴sin(-2π-α)=-sin
α=-,故选B.
答案 B
3.已知sin=,则cos的值等于( ).
A.-
B.
C.
D.
解析 cos=sin=sin=-sin=-.
答案 A
4.若cos(π-x)=,x∈(-π,π),则x的值为________.
解析 ∵cos(π-x)=,∴cos
x=-.∵x∈(-π,π),∴x=±.
答案 ±
5.若|sin
α|=sin(-π+α),则α的取值范围是________.
解析 ∵|sin
α|=sin(-π+α)=-sin
α,∴sinα≤0,
∴α的取值范围为[π+2kπ,2π+2kπ](k∈Z).
答案 [π+2kπ,2π+2kπ](k∈Z)
6.(1)求值:sin
1
200°cos
1
290°+cos(-1
020°)sin(-1
050°);
(2)已知cos=,求sin的值.
解 (1)原式=sin(3×360°+120°)·cos(3×360°+210°)+cos(-3×360°+60°)·sin(-3×360°+30°)
=sin
120°cos
210°+cos
60°sin
30°
=-sin
60°cos
30°+cos
60°sin
30°
=-×+×
=-.
(2)∵π-α=+
∴sin=sin
=cos=.
综合提高 限时25分钟
7.若sin(π+α)+cos=-m,则cos+2sin(2π-α)的值为( ).
A.-m
B.m
C.-m
D.m
解析 ∵sin(π+α)+cos=-sin
α-sin
α=-m,∴sin
α=,
∴cos+2sin
(2π-α)=-sin
α-2sin
α=-3sin
α=-3×=-m.
答案 C
8.α和β的终边关于y轴对称,下列各式中正确的是( ).
A.sin
α=sin
β
B.cos
α=cos
β
C.cos(π-α)=cos
β
D.sin(π-α)=-sin
β
解析 ∵α和β的终边关于y轴对称,
∴β与π-α终边相同,
∴β=2kπ+π-α,k∈Z,
∴sin
β=sin(2kπ+π-α)=sin(π-α)=sin
α.
答案 A
9.已知sin=,则cos=________.
解析 ∵+=,
∴cos=cos
=sin=,
∴应填.
答案
10.已知f(x)=则f+f=________.
解析 ∵f=sin=sin
=,f=f-1=f-2=sin-2=-,∴f+f=-=-2.
答案 -2
11.设f(n)=cos(n∈N
),求f(1)+f(2)+f(3)+…+f(2
011)的值.
解 f(1)+f(2)+f(3)+f(4)
=cos++cosπ++cos++cos2π+
=-sin
-cos
+sin
+cos
=0.
∴f(1)+f(2)+…+f(2
008)
=502[f(1)+f(2)+f(3)+f(4)]=0.
∴f(1)+f(2)+…+f(2
011)=f(2
009)+f(2
010)+f(2
011)
=cos+cos+cosπ+
=cos+cos+cos
=-sin
-cos
-cos
π
=--+=-.
12.(创新拓展)已知A、B、C为△ABC的三个内角,求证:
(1)cos(2A+B+C)=cos(B+C);
(2)sin=cos.
证明 (1)∵左式=cos(2A+B+C)=cos[A+(A+B+C)]=cos(π+A)=-cos
A,
右式=cos(B+C)=cos(π-A)=-cos
A,
左式=右式,∴cos(2A+B+C)=cos(B+C).
(2)右式=cos=cos
=cos=cos
=sin
=左式.
∴sin=cos.
单位圆与诱导公式
同步练习
双基达标 限时20分钟
1.sin
π的值为( ).
A.-
B.
C.-
D.
解析 sin
π=sin=sin
=.
答案 B
2.已知cos(π-α)=-,且α是第一象限角,则sin(-2π-α)的值是( ).
A.
B.-
C.±
D.
解析 ∵cos(π-α)=-,∴cos
α=.
∵α是第一象限角,∴sin
α=.
∴sin(-2π-α)=-sin
α=-,故选B.
答案 B
3.已知sin=,则cos的值等于( ).
A.-
B.
C.
D.
解析 cos=sin=sin=-sin=-.
答案 A
4.若cos(π-x)=,x∈(-π,π),则x的值为________.
解析 ∵cos(π-x)=,∴cos
x=-.∵x∈(-π,π),∴x=±.
答案 ±
5.若|sin
α|=sin(-π+α),则α的取值范围是________.
解析 ∵|sin
α|=sin(-π+α)=-sin
α,∴sinα≤0,
∴α的取值范围为[π+2kπ,2π+2kπ](k∈Z).
答案 [π+2kπ,2π+2kπ](k∈Z)
6.(1)求值:sin
1
200°cos
1
290°+cos(-1
020°)sin(-1
050°);
(2)已知cos=,求sin的值.
解 (1)原式=sin(3×360°+120°)·cos(3×360°+210°)+cos(-3×360°+60°)·sin(-3×360°+30°)
=sin
120°cos
210°+cos
60°sin
30°
=-sin
60°cos
30°+cos
60°sin
30°
=-×+×
=-.
(2)∵π-α=+
∴sin=sin
=cos=.
综合提高 限时25分钟
7.若sin(π+α)+cos=-m,则cos+2sin(2π-α)的值为( ).
A.-m
B.m
C.-m
D.m
解析 ∵sin(π+α)+cos=-sin
α-sin
α=-m,∴sin
α=,
∴cos+2sin
(2π-α)=-sin
α-2sin
α=-3sin
α=-3×=-m.
答案 C
8.α和β的终边关于y轴对称,下列各式中正确的是( ).
A.sin
α=sin
β
B.cos
α=cos
β
C.cos(π-α)=cos
β
D.sin(π-α)=-sin
β
解析 ∵α和β的终边关于y轴对称,
∴β与π-α终边相同,
∴β=2kπ+π-α,k∈Z,
∴sin
β=sin(2kπ+π-α)=sin(π-α)=sin
α.
答案 A
9.已知sin=,则cos=________.
解析 ∵+=,
∴cos=cos
=sin=,
∴应填.
答案
10.已知f(x)=则f+f=________.
解析 ∵f=sin=sin
=,f=f-1=f-2=sin-2=-,∴f+f=-=-2.
答案 -2
11.设f(n)=cos(n∈N
),求f(1)+f(2)+f(3)+…+f(2
011)的值.
解 f(1)+f(2)+f(3)+f(4)
=cos++cosπ++cos++cos2π+
=-sin
-cos
+sin
+cos
=0.
∴f(1)+f(2)+…+f(2
008)
=502[f(1)+f(2)+f(3)+f(4)]=0.
∴f(1)+f(2)+…+f(2
011)=f(2
009)+f(2
010)+f(2
011)
=cos+cos+cosπ+
=cos+cos+cos
=-sin
-cos
-cos
π
=--+=-.
12.(创新拓展)已知A、B、C为△ABC的三个内角,求证:
(1)cos(2A+B+C)=cos(B+C);
(2)sin=cos.
证明 (1)∵左式=cos(2A+B+C)=cos[A+(A+B+C)]=cos(π+A)=-cos
A,
右式=cos(B+C)=cos(π-A)=-cos
A,
左式=右式,∴cos(2A+B+C)=cos(B+C).
(2)右式=cos=cos
=cos=cos
=sin
=左式.
∴sin=cos.
