1.7.1-1.7.2 正切函数的定义、图像和性质 同步练习(含答案)
文档属性
| 名称 | 1.7.1-1.7.2 正切函数的定义、图像和性质 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 00:00:00 | ||
图片预览


文档简介
1.7.1-1.7.2
正切函数的定义、图像和性质
同步练习
一、选择题
1.若角α的终边上有一点P(2x-1,3),且tanα=,则x的值为( )
A.
7
B.
8
C.
15
D.
解析 由=,得x=8.
答案 B
2.函数y=的定义域为( )
A.
B.
C.
D.
解析 由logtanx≥0知0答案 C
3.以下三个描述不正确的有( )
①正切函数为定义域上的增函数;②正切函数存在闭区间[a,b],使y=tanx在其上是递增的;③正切函数存在闭区间[a,b],使y=tanx在其上是递减的.
A.0个
B.1个
C.2个
D.3个
解析 只有②正确.
答案 B
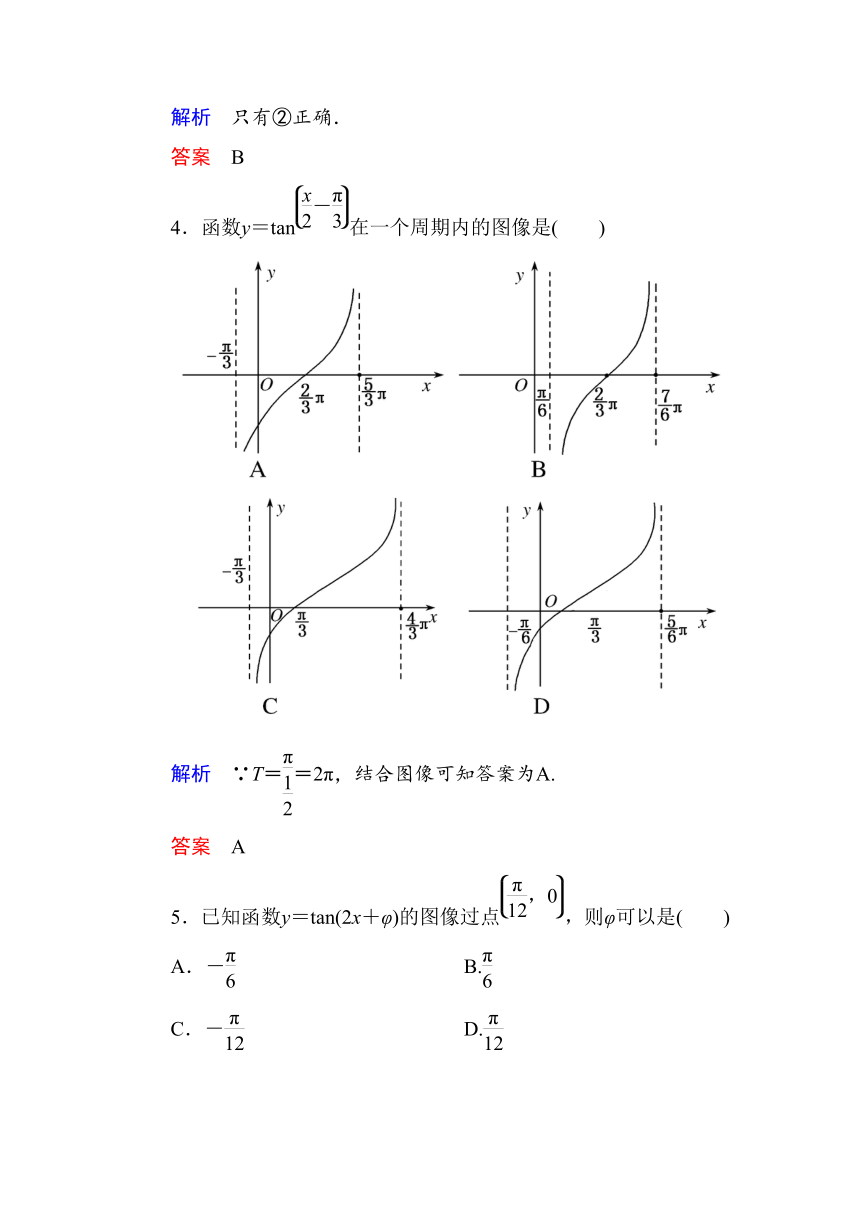
4.函数y=tan在一个周期内的图像是( )
解析 ∵T==2π,结合图像可知答案为A.
答案 A
5.已知函数y=tan(2x+φ)的图像过点,则φ可以是( )
A.-
B.
C.-
D.
解析 由题意得tan(+φ)=0,即tan(+φ)=0,且+φ=kπ,∴φ=kπ-,令k=0,则φ=-.
答案 A
6.在区间范围内,函数y=tanx与函数y=sinx的图像交点的个数为( )
A.1
B.2
C.3
D.4
解析 方法一:在同一坐标系中,首先作出y=sinx与y=tanx在内的图像,需明确x∈时,有sinx<x<tanx(利用单位圆中的正弦线、正切线就可以证明),然后利用对称性作出x∈的两函数的图像如图,由图像可知它们有3个交点.
∴应选C.
方法二:x∈,
即sinx=tanx=,sinx=0,sinx=0或cosx=1.
在x∈内x=-π、0、π满足sinx=0,
x=0满足cosx=1,所以交点个数为3.
∴应选C.
答案 C
7.已知函数f(x)=Atan(ωx+φ),y=f(x)的部分图像如图所示,则f=( )
A.
2+
B.
C.
D.
2-
解析 由图可知T==2=,
∴ω=2,由2×π+φ=kπ,k∈Z,|φ|<,知φ=,由Atan=1,知A=1,
∴f(x)=tan,∴f=tan=.
答案 B
二、填空题
8.已知θ∈,在单位圆中,角θ的正弦线、余弦线、正切线分别是a、b、c,则它们的大小关系是__________.
解析 由三角函数线知c>a>b.
答案 c>a>b
9.函数y=的值域为________.
解析 设u=tan2x-2tanx+2=(tanx-1)2+1,显然u≥1,由反比例函数的图像可知值域为(0,1].
答案 (0,1]
10.若y=tan(2x+θ)图像的一个对称中心为,其中-<θ<,则θ=________.
解析 由题意得2x+θ=(k∈Z),得x=-,
∵y=tan(2x+θ)的一个对称中心为,
∴-=,∴θ=-π.
又θ∈,∴θ=,或θ=-.
答案 或-
三、解答题
11.作出函数f(x)=tanx+|tanx|的图像,并求出其周期.
解析 f(x)=tanx+|tanx|=
(k∈Z).作出f(x)的图像如下图,易得函数f(x)的周期T=π.
12.已知f(x)=tan,
(1)求f(x)的定义域及值域;
(2)求f(x)的周期及单调增区间.
解 (1)由2x+≠kπ+(k∈Z),
得x≠+(k∈Z),
∴函数的定义域为,
由正切函数的图像可知值域为R.
(2)f(x)的周期T=,
由kπ-<2x+得-π故函数的单调增区间为(k∈Z).
13.确定函数f(x)=sinx+tanx,x∈的奇偶性、单调性,并求出它的值域.
解 显然f(x)的定义域关于原点对称,又f(-x)=sin(-x)+tan(-x)=-sinx-tanx=-f(x),
∴f(x)为奇函数,设-≤x1∵y=sinx和y=tanx在区间上都是增函数,
∴sinx1∴sinx1+tanx1即f(x1)∴f(x)在上是增函数.
∴f(x)在上的值域为.
正切函数的定义、图像和性质
同步练习
一、选择题
1.若角α的终边上有一点P(2x-1,3),且tanα=,则x的值为( )
A.
7
B.
8
C.
15
D.
解析 由=,得x=8.
答案 B
2.函数y=的定义域为( )
A.
B.
C.
D.
解析 由logtanx≥0知0
3.以下三个描述不正确的有( )
①正切函数为定义域上的增函数;②正切函数存在闭区间[a,b],使y=tanx在其上是递增的;③正切函数存在闭区间[a,b],使y=tanx在其上是递减的.
A.0个
B.1个
C.2个
D.3个
解析 只有②正确.
答案 B
4.函数y=tan在一个周期内的图像是( )
解析 ∵T==2π,结合图像可知答案为A.
答案 A
5.已知函数y=tan(2x+φ)的图像过点,则φ可以是( )
A.-
B.
C.-
D.
解析 由题意得tan(+φ)=0,即tan(+φ)=0,且+φ=kπ,∴φ=kπ-,令k=0,则φ=-.
答案 A
6.在区间范围内,函数y=tanx与函数y=sinx的图像交点的个数为( )
A.1
B.2
C.3
D.4
解析 方法一:在同一坐标系中,首先作出y=sinx与y=tanx在内的图像,需明确x∈时,有sinx<x<tanx(利用单位圆中的正弦线、正切线就可以证明),然后利用对称性作出x∈的两函数的图像如图,由图像可知它们有3个交点.
∴应选C.
方法二:x∈,
即sinx=tanx=,sinx=0,sinx=0或cosx=1.
在x∈内x=-π、0、π满足sinx=0,
x=0满足cosx=1,所以交点个数为3.
∴应选C.
答案 C
7.已知函数f(x)=Atan(ωx+φ),y=f(x)的部分图像如图所示,则f=( )
A.
2+
B.
C.
D.
2-
解析 由图可知T==2=,
∴ω=2,由2×π+φ=kπ,k∈Z,|φ|<,知φ=,由Atan=1,知A=1,
∴f(x)=tan,∴f=tan=.
答案 B
二、填空题
8.已知θ∈,在单位圆中,角θ的正弦线、余弦线、正切线分别是a、b、c,则它们的大小关系是__________.
解析 由三角函数线知c>a>b.
答案 c>a>b
9.函数y=的值域为________.
解析 设u=tan2x-2tanx+2=(tanx-1)2+1,显然u≥1,由反比例函数的图像可知值域为(0,1].
答案 (0,1]
10.若y=tan(2x+θ)图像的一个对称中心为,其中-<θ<,则θ=________.
解析 由题意得2x+θ=(k∈Z),得x=-,
∵y=tan(2x+θ)的一个对称中心为,
∴-=,∴θ=-π.
又θ∈,∴θ=,或θ=-.
答案 或-
三、解答题
11.作出函数f(x)=tanx+|tanx|的图像,并求出其周期.
解析 f(x)=tanx+|tanx|=
(k∈Z).作出f(x)的图像如下图,易得函数f(x)的周期T=π.
12.已知f(x)=tan,
(1)求f(x)的定义域及值域;
(2)求f(x)的周期及单调增区间.
解 (1)由2x+≠kπ+(k∈Z),
得x≠+(k∈Z),
∴函数的定义域为,
由正切函数的图像可知值域为R.
(2)f(x)的周期T=,
由kπ-<2x+
13.确定函数f(x)=sinx+tanx,x∈的奇偶性、单调性,并求出它的值域.
解 显然f(x)的定义域关于原点对称,又f(-x)=sin(-x)+tan(-x)=-sinx-tanx=-f(x),
∴f(x)为奇函数,设-≤x1
∴sinx1
∴f(x)在上的值域为.
