1.7.3 正切函数的诱导公式 同步练习2(含答案)
文档属性
| 名称 | 1.7.3 正切函数的诱导公式 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 123.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 00:00:00 | ||
图片预览


文档简介
1.7.3
正切函数的诱导公式
同步练习
一、选择题
1.若f(x)=tanx,则f(600°)的值为( )
A.
B.-
C.
D.-
解析 f(600°)=tan600°=tan60°=.
答案 C
2.tanπ+tan的值为( )
A.-
B.0
C.
D.-
解析 tanπ+tan=tan
-tan=tanπ-tan=-2tan
=-.
答案 D
3.若sin(π+α)=-,则sintan(π-α)的值为( )
A.
B.
-
C.
D.
-
解析 由sin(π+α)=-,知sinα=.
又sin·tan(π-α)=cosα
=-sinα=-.
答案 B
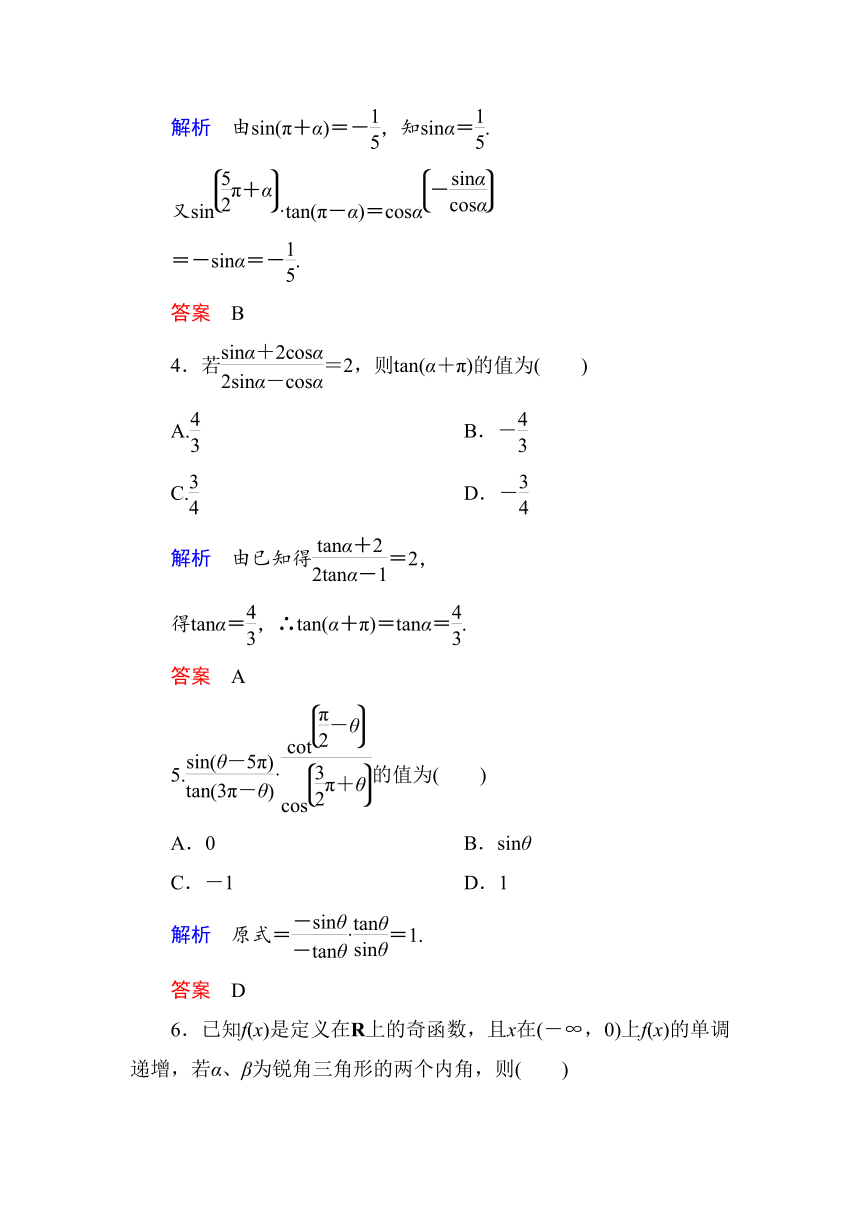
4.若=2,则tan(α+π)的值为( )
A.
B.-
C.
D.-
解析 由已知得=2,
得tanα=,∴tan(α+π)=tanα=.
答案 A
5.·的值为( )
A.0
B.sinθ
C.-1
D.1
解析 原式=·=1.
答案 D
6.已知f(x)是定义在R上的奇函数,且x在(-∞,0)上f(x)的单调递增,若α、β为锐角三角形的两个内角,则( )
A.f(tanα)>f(tanβ)
B.
f(tanα)<f(tanβ)
C.f(tanα)>f(cotβ)
D.f(tanα)>f(cotβ)
解析 ∵α、β为锐角三角形的两个内角,
∴α+β>,∴α>-β,又α、β∈
∴tanα>tan,即tanα>cotβ,
又f(x)为奇函数,且在(-∞,0)上单调递增,
∴f(x)在(0,+∞)上单调递增,
故f(tanα)>f(cotβ).
答案 C
二、填空题
7.已知tan=m(m≠0),则cot的值为________.
解析 ∵(-2α)+(2α+π)=π,
∴cot(2α+π)=-cot(-2α)=-.
答案 -
8.tan(27°-α)·tan(49°-β)·tan(63°+α)·tan(139°-β)=________.
解析 ∵(27°-α)+(63°+α)=90°,
∴tan(27°-α)·tan(63°+α)=1。
又(139°-β)-(49°-β)=90°,
∴tan(139°-β)·tan(49°-β)=-1,故原式=-1.
答案 -1
9.=________.
解析 原式=
==.
答案
三、解答题
10.已知sin(π+α)=-,0<α<,求:
sin·tan的值.
解:∵sin(π+α)=-,∴-sinα=-,
即sinα=.
即cosα=,tanα==,cotα=2.
∴sin·tan=-cosα·tan=cosα·cotα=·2=.
11.已知α为第二象限角,且tanα-=,
求的值.
解 由tanα-=,得4tan2α-15tanα-4=0,
得tanα=-或tanα=4.
又α为第二象限的角,∴tanα=-.
故==
=.
12.求tan2-tan2(n∈Z)的值.
解 ∵tan=tan,
tan=tan,
∴原式=tan2-tan2
=tan2-tan2=
cot2α-cot2α=0.
13.已知角α的终边经过点P(4,-3),
(1)求sinα,cosα,tanα的值;
(2)求·的值.
解 (1)∵r==5,
∴sinα==-,
cosα==,tanα==-.
(2)·
=·=-
=-=-.
正切函数的诱导公式
同步练习
一、选择题
1.若f(x)=tanx,则f(600°)的值为( )
A.
B.-
C.
D.-
解析 f(600°)=tan600°=tan60°=.
答案 C
2.tanπ+tan的值为( )
A.-
B.0
C.
D.-
解析 tanπ+tan=tan
-tan=tanπ-tan=-2tan
=-.
答案 D
3.若sin(π+α)=-,则sintan(π-α)的值为( )
A.
B.
-
C.
D.
-
解析 由sin(π+α)=-,知sinα=.
又sin·tan(π-α)=cosα
=-sinα=-.
答案 B
4.若=2,则tan(α+π)的值为( )
A.
B.-
C.
D.-
解析 由已知得=2,
得tanα=,∴tan(α+π)=tanα=.
答案 A
5.·的值为( )
A.0
B.sinθ
C.-1
D.1
解析 原式=·=1.
答案 D
6.已知f(x)是定义在R上的奇函数,且x在(-∞,0)上f(x)的单调递增,若α、β为锐角三角形的两个内角,则( )
A.f(tanα)>f(tanβ)
B.
f(tanα)<f(tanβ)
C.f(tanα)>f(cotβ)
D.f(tanα)>f(cotβ)
解析 ∵α、β为锐角三角形的两个内角,
∴α+β>,∴α>-β,又α、β∈
∴tanα>tan,即tanα>cotβ,
又f(x)为奇函数,且在(-∞,0)上单调递增,
∴f(x)在(0,+∞)上单调递增,
故f(tanα)>f(cotβ).
答案 C
二、填空题
7.已知tan=m(m≠0),则cot的值为________.
解析 ∵(-2α)+(2α+π)=π,
∴cot(2α+π)=-cot(-2α)=-.
答案 -
8.tan(27°-α)·tan(49°-β)·tan(63°+α)·tan(139°-β)=________.
解析 ∵(27°-α)+(63°+α)=90°,
∴tan(27°-α)·tan(63°+α)=1。
又(139°-β)-(49°-β)=90°,
∴tan(139°-β)·tan(49°-β)=-1,故原式=-1.
答案 -1
9.=________.
解析 原式=
==.
答案
三、解答题
10.已知sin(π+α)=-,0<α<,求:
sin·tan的值.
解:∵sin(π+α)=-,∴-sinα=-,
即sinα=.
即cosα=,tanα==,cotα=2.
∴sin·tan=-cosα·tan=cosα·cotα=·2=.
11.已知α为第二象限角,且tanα-=,
求的值.
解 由tanα-=,得4tan2α-15tanα-4=0,
得tanα=-或tanα=4.
又α为第二象限的角,∴tanα=-.
故==
=.
12.求tan2-tan2(n∈Z)的值.
解 ∵tan=tan,
tan=tan,
∴原式=tan2-tan2
=tan2-tan2=
cot2α-cot2α=0.
13.已知角α的终边经过点P(4,-3),
(1)求sinα,cosα,tanα的值;
(2)求·的值.
解 (1)∵r==5,
∴sinα==-,
cosα==,tanα==-.
(2)·
=·=-
=-=-.
