1.8 函数y=Asin(ωx+ψ)的图像 同步练习1(含答案)
文档属性
| 名称 | 1.8 函数y=Asin(ωx+ψ)的图像 同步练习1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 329.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 00:00:00 | ||
图片预览




文档简介
1.8
函数y=Asin(ωx+ψ)的图像
同步练习
基础巩固训练(30分钟
50分)
一、选择题(每小题4分,共16分)
1.函数y=sin的图像可由函数y=sinx的图像 ( )
A.向左平移个单位得到
B.向右平移个单位得到
C.向左平移个单位得到
D.向左平移个单位得到
【解析】选A.y=sin=sin,故应向左平移个单位.
2.由y=f(x)的图像向左平移个单位,再把所得图像上所有点的横坐标伸长到原来的2倍得到y=2sin的图像,则f(x)为
( )
A.2sin
B.2sin
C.2sin
D.2sin
【解析】选B.将y=2sin图像上所有点的横坐标缩短到原来的倍得到y=2sin,再将图像向右平移个单位,得到y=2sin.
【误区警示】本题容易出现将平移方向、倍数弄反的错误,应将图像逆向变换得到平移前的图像.
【变式训练】函数y=
f(x)的图像上每一点的纵坐标伸长为原来的3倍,再将横坐标缩小为原来的,再将图像向右平移个单位,可得y=cosx,则原来的函数为
( )
A.y=cos
B.y=cos
C.y=3cos
D.y=cos
【解析】选A.将y=cosx的图像向左平移个单位,得到y=cos,再将横坐标伸长为原来的2倍,得到y=cos,再将图像上每一点的纵坐标缩短为原来的倍,得到y=cos.
3.函数y=sinωx(ω>0)的部分图像如图所示,点A,B是最高点,点C是最低点.若△ABC是直角三角形,则ω的值为 ( )
A.
B.
C.
D.π
【解析】选A.函数的最大值为1,又△ABC是等腰直角三角形,故三角形AB边上的高为2,A与B的距离为4,即为最小正周期T,由=4得ω=.
【误区警示】读图错误,误认为|AB|=2,从而=2,ω=π,选D.
4.函数y=sin(ωx+φ)的部分图像如图,则 ( )
A.ω=,φ=
B.ω=,φ=
C.ω=,φ=
D.ω=,φ=
【解析】选C.由题意以及函数的图像,可知T=4×(3-1)=8,
因为T=,所以ω=;
因为函数的图像经过(3,0),
所以0=sin且0≤φ<π,
所以φ=.故选C.
二、填空题(每小题5分,共10分)
5.函数f
(x)=sin(ωx+φ)的图像如图所示,为了得到y=sinωx的图像,只需把y=f(x)的图像上所有的点向右平移
个单位长度.
【解析】T=4=π,故ω=2,
则f(x)=sin(2x+φ),代入点,
得到sin=0,
由+φ=π得φ=,
故f(x)=sin,
故需要向右平移个单位长度得到y=sin2x.
答案:
6.若将函数f(x)=sin的图像向右平移φ个单位,所得图像关于y轴对称,则φ的最小正值是 .
【解题指南】平移后的函数是余弦函数.
【解析】将函数f(x)=sin的图像向右平移φ个单位,
所得函数为f(x)=sin
=sin,
其图像关于y轴对称,则f(x)=±cos2x,
所以-2φ=+kπ(k∈Z),
当k=-1时,φ的最小正值是.
答案:
三、解答题(每小题12分,共24分)
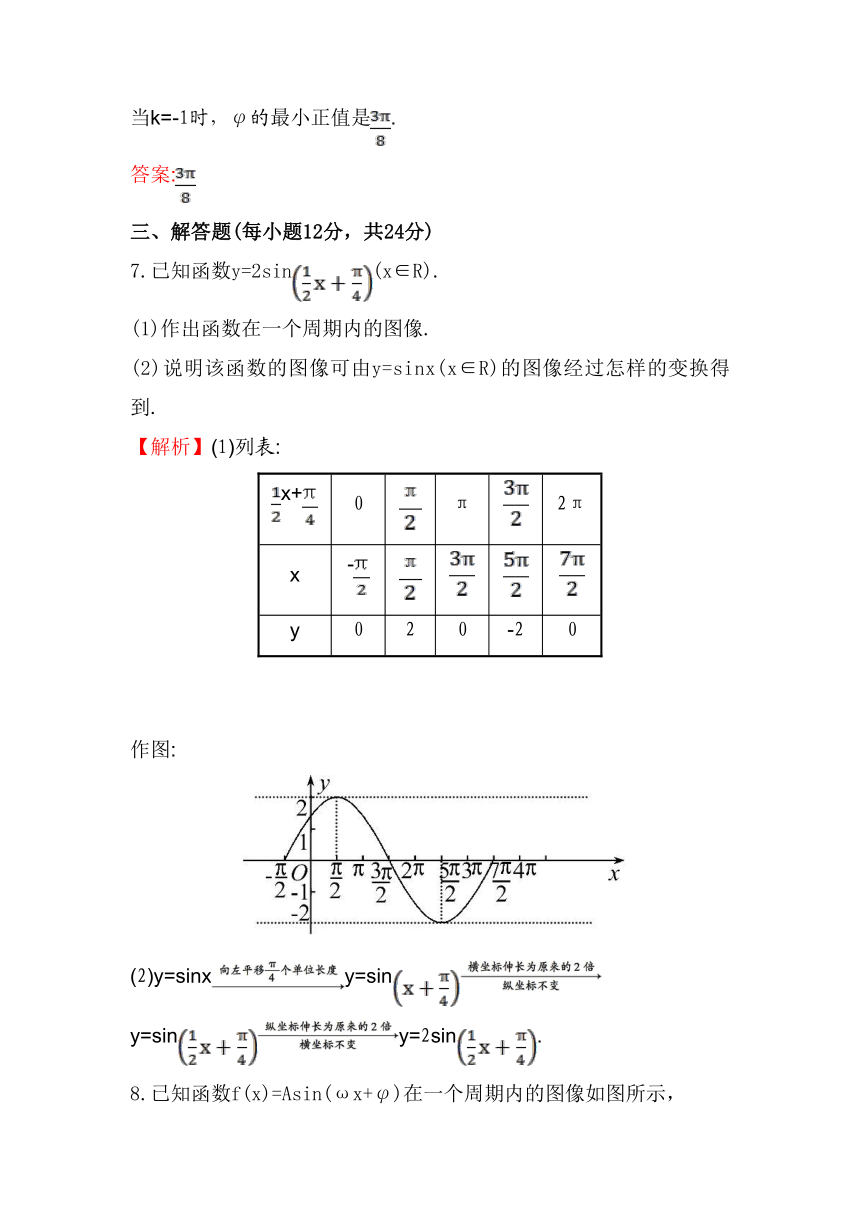
7.已知函数y=2sin(x∈R).
(1)作出函数在一个周期内的图像.
(2)说明该函数的图像可由y=sinx(x∈R)的图像经过怎样的变换得到.
【解析】(1)列表:
x+
0
π
2π
x
-
y
0
2
0
-2
0
作图:
(2)y=sinxy=sin
y=siny=2sin.
8.已知函数f(x)=Asin(ωx+φ)在一个周期内的图像如图所示,
(1)求f(x)的解析式.
(2)求f+f+f+…+f的值.
【解题指南】根据图示信息求出解析式,再根据函数在一个周期内的和的情况求和.
【解析】(1)由图像可知A=2,
周期T=2=π,
所以ω===2,
则f(x)=2sin(2x+φ),
由图像过点,
得2sin=2,
即sin=1,
取+φ=得φ=,
故f(x)=2sin.
(2)由(1)可知f(x)的周期为π,
因为f+f+f+f=1--1+=0,
所以f+f+f+…+f=0×503+f+f+f
=f+f+f=1--1=-.
能力提升训练(30分钟
50分)
一、选择题(每小题4分,共12分)
1.已知函数f(x)=Asin(ωx+φ)在一个周期内的图像如图所示,则y=f(x)的图像可由函数y=cosx的图像(纵坐标不变), 得到 ( )
A.先把各点的横坐标缩短到原来的倍,再向左平移个单位长度
B.先把各点的横坐标缩短到原来的倍,再向右平移个单位长度
C.先把各点的横坐标伸长到原来的2倍,再向左平移个单位长度
D.先把各点的横坐标伸长到原来的2倍,再向右平移个单位长度
【解析】选B.由图可知A=1,T=4×=π,
故ω=2,则f=sin,
又图像过,故sin=1,
故由+φ=,得φ=,
故f=sin,
又f=sin=cos
=cos,
故将函数y=cosx的图像先把各点的横坐标缩短到原来的倍,再向右平移个单位长度得到f=sin的图像.
2.要得到函数y=sin(3x-2)的图像,只要将函数y=sin3x的图像 ( )
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】选D.由y=sin3=sin,故应向右平移个单位长度.
【变式训练】要得到函数y=cos2x的图像,只需将y=cos的图像 ( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】选B.设将y=cos的图像向右平移A个单位长度后,得到函数y=cos2x的图像,则cos=cos2x,易得A=,故选B.
3.已知函数y=Asin(ωx+φ)+B的一部分图像如图所示,如果A>0,ω>0,|φ|<,则 ( )
A.A=4
B.ω=1
C.φ=
D.B=4
【解析】选C.根据函数的最大值和最小值得求得A=2,B=2,
函数的周期为×4=π,即π=,ω=2,
当x=时取最大值,即sin=1,
2×+φ=2kπ+,φ=2kπ+,
又|φ|<,所以φ=.
【拓展延伸】已知函数y=Asin+B的部分图像求解析式
观察图像的性质,确定函数的最大值M,最小值m,则
A=,B=,
ω:先求周期后求ω;
φ:代入图像上一个点的坐标求出φ的取值集合,根据φ的范围求φ.
二、填空题(每小题4分,共8分)
4.若y=Asin(ωx+φ)的最小值为-2,其图像相邻最高点与最低点横坐标之差为3π,又图像过点(0,1),则其解析式是 .
【解析】由最小值为-2可得A=2,
由题意T=6π=,故ω=,则y=2sin,
又sinφ=,|φ|<,故φ=,
所以y=2sin.
答案:y=2sin
5.将函数f(x)=sin(ωx+φ)图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图像,则f= .
【解题指南】先根据三角函数图像变换求出ω,φ的值,然后求出f的值.
【解析】函数f(x)=sin(ωx+φ)图像上每一点的横坐标缩短为原来的一半,纵坐标不变,则函数变为y=sin(2ωx+φ),再向右平移个单位长度得到的函数为y=sin=sin=sinx,
所以
又因为ω>0,-≤φ<,
可求得ω=,φ=,
所以f(x)=sin,
所以f=sin=sin=.
答案:
【变式训练】将函数y=sinωx(ω>0)的图像向左平移个单位,平移后的图像如图所示,则平移后的图像所对应函数的解析式是 .
【解题指南】先用ω表示出平移后的解析式,再利用图中已知的相位求出ω即可求出解析式.
【解析】函数y=sinωx(ω>0)的图像向左平移个单位得到y=sin,
则πω+=,解得ω=2,
故平移后的图像的解析式为y=sin.
答案:y=sin
三、解答题(每小题10分,共20分)
6.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的最小正周期为,最小值为-2,图像过,求该函数的解析式.
【解析】因为函数的最小正周期为,
所以T==,即ω=3.
又因为函数的最小值为-2,
所以A=2,
所以函数解析式可写为y=2sin,
又因为函数图像过点,
所以有:2sin=0,
解得φ=kπ-.
因为|φ|<π,
所以φ=或-,
所以,函数解析式为:y=2sin或y=2sin.
7.将函数y=lgx的图像向左平移一个单位长度,可得函数f(x)的图像;将函数y=cos的图像向左平移个单位长度,可得函数g(x)的图像.
(1)在同一直角坐标系中画出函数f(x)和g(x)的图像.
(2)判断方程f(x)=g(x)解的个数.
【解题指南】解答本题(1)利用平移变换法画出两个函数的图像.(2)根据弦函数的“有界性”及lg10=1确定两个函数图像的交点个数,即为方程f(x)=g(x)解的个数.
【解析】函数y=lgx的图像向左平移一个单位长度,可得函数f(x)=lg(x+1)的图像,即图像C1;函数y=cos的图像向左平移个单位长度,可得函数g(x)=cos=cos2x的图像,即图像C2.
(1)画出图像C1和C2如图.
(2)因为f(9)=lg10=1,
所以由图像可知:两个图像共有5个交点.
即方程f(x)=g(x)解的个数为5.
函数y=Asin(ωx+ψ)的图像
同步练习
基础巩固训练(30分钟
50分)
一、选择题(每小题4分,共16分)
1.函数y=sin的图像可由函数y=sinx的图像 ( )
A.向左平移个单位得到
B.向右平移个单位得到
C.向左平移个单位得到
D.向左平移个单位得到
【解析】选A.y=sin=sin,故应向左平移个单位.
2.由y=f(x)的图像向左平移个单位,再把所得图像上所有点的横坐标伸长到原来的2倍得到y=2sin的图像,则f(x)为
( )
A.2sin
B.2sin
C.2sin
D.2sin
【解析】选B.将y=2sin图像上所有点的横坐标缩短到原来的倍得到y=2sin,再将图像向右平移个单位,得到y=2sin.
【误区警示】本题容易出现将平移方向、倍数弄反的错误,应将图像逆向变换得到平移前的图像.
【变式训练】函数y=
f(x)的图像上每一点的纵坐标伸长为原来的3倍,再将横坐标缩小为原来的,再将图像向右平移个单位,可得y=cosx,则原来的函数为
( )
A.y=cos
B.y=cos
C.y=3cos
D.y=cos
【解析】选A.将y=cosx的图像向左平移个单位,得到y=cos,再将横坐标伸长为原来的2倍,得到y=cos,再将图像上每一点的纵坐标缩短为原来的倍,得到y=cos.
3.函数y=sinωx(ω>0)的部分图像如图所示,点A,B是最高点,点C是最低点.若△ABC是直角三角形,则ω的值为 ( )
A.
B.
C.
D.π
【解析】选A.函数的最大值为1,又△ABC是等腰直角三角形,故三角形AB边上的高为2,A与B的距离为4,即为最小正周期T,由=4得ω=.
【误区警示】读图错误,误认为|AB|=2,从而=2,ω=π,选D.
4.函数y=sin(ωx+φ)的部分图像如图,则 ( )
A.ω=,φ=
B.ω=,φ=
C.ω=,φ=
D.ω=,φ=
【解析】选C.由题意以及函数的图像,可知T=4×(3-1)=8,
因为T=,所以ω=;
因为函数的图像经过(3,0),
所以0=sin且0≤φ<π,
所以φ=.故选C.
二、填空题(每小题5分,共10分)
5.函数f
(x)=sin(ωx+φ)的图像如图所示,为了得到y=sinωx的图像,只需把y=f(x)的图像上所有的点向右平移
个单位长度.
【解析】T=4=π,故ω=2,
则f(x)=sin(2x+φ),代入点,
得到sin=0,
由+φ=π得φ=,
故f(x)=sin,
故需要向右平移个单位长度得到y=sin2x.
答案:
6.若将函数f(x)=sin的图像向右平移φ个单位,所得图像关于y轴对称,则φ的最小正值是 .
【解题指南】平移后的函数是余弦函数.
【解析】将函数f(x)=sin的图像向右平移φ个单位,
所得函数为f(x)=sin
=sin,
其图像关于y轴对称,则f(x)=±cos2x,
所以-2φ=+kπ(k∈Z),
当k=-1时,φ的最小正值是.
答案:
三、解答题(每小题12分,共24分)
7.已知函数y=2sin(x∈R).
(1)作出函数在一个周期内的图像.
(2)说明该函数的图像可由y=sinx(x∈R)的图像经过怎样的变换得到.
【解析】(1)列表:
x+
0
π
2π
x
-
y
0
2
0
-2
0
作图:
(2)y=sinxy=sin
y=siny=2sin.
8.已知函数f(x)=Asin(ωx+φ)在一个周期内的图像如图所示,
(1)求f(x)的解析式.
(2)求f+f+f+…+f的值.
【解题指南】根据图示信息求出解析式,再根据函数在一个周期内的和的情况求和.
【解析】(1)由图像可知A=2,
周期T=2=π,
所以ω===2,
则f(x)=2sin(2x+φ),
由图像过点,
得2sin=2,
即sin=1,
取+φ=得φ=,
故f(x)=2sin.
(2)由(1)可知f(x)的周期为π,
因为f+f+f+f=1--1+=0,
所以f+f+f+…+f=0×503+f+f+f
=f+f+f=1--1=-.
能力提升训练(30分钟
50分)
一、选择题(每小题4分,共12分)
1.已知函数f(x)=Asin(ωx+φ)在一个周期内的图像如图所示,则y=f(x)的图像可由函数y=cosx的图像(纵坐标不变), 得到 ( )
A.先把各点的横坐标缩短到原来的倍,再向左平移个单位长度
B.先把各点的横坐标缩短到原来的倍,再向右平移个单位长度
C.先把各点的横坐标伸长到原来的2倍,再向左平移个单位长度
D.先把各点的横坐标伸长到原来的2倍,再向右平移个单位长度
【解析】选B.由图可知A=1,T=4×=π,
故ω=2,则f=sin,
又图像过,故sin=1,
故由+φ=,得φ=,
故f=sin,
又f=sin=cos
=cos,
故将函数y=cosx的图像先把各点的横坐标缩短到原来的倍,再向右平移个单位长度得到f=sin的图像.
2.要得到函数y=sin(3x-2)的图像,只要将函数y=sin3x的图像 ( )
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】选D.由y=sin3=sin,故应向右平移个单位长度.
【变式训练】要得到函数y=cos2x的图像,只需将y=cos的图像 ( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】选B.设将y=cos的图像向右平移A个单位长度后,得到函数y=cos2x的图像,则cos=cos2x,易得A=,故选B.
3.已知函数y=Asin(ωx+φ)+B的一部分图像如图所示,如果A>0,ω>0,|φ|<,则 ( )
A.A=4
B.ω=1
C.φ=
D.B=4
【解析】选C.根据函数的最大值和最小值得求得A=2,B=2,
函数的周期为×4=π,即π=,ω=2,
当x=时取最大值,即sin=1,
2×+φ=2kπ+,φ=2kπ+,
又|φ|<,所以φ=.
【拓展延伸】已知函数y=Asin+B的部分图像求解析式
观察图像的性质,确定函数的最大值M,最小值m,则
A=,B=,
ω:先求周期后求ω;
φ:代入图像上一个点的坐标求出φ的取值集合,根据φ的范围求φ.
二、填空题(每小题4分,共8分)
4.若y=Asin(ωx+φ)的最小值为-2,其图像相邻最高点与最低点横坐标之差为3π,又图像过点(0,1),则其解析式是 .
【解析】由最小值为-2可得A=2,
由题意T=6π=,故ω=,则y=2sin,
又sinφ=,|φ|<,故φ=,
所以y=2sin.
答案:y=2sin
5.将函数f(x)=sin(ωx+φ)图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sinx的图像,则f= .
【解题指南】先根据三角函数图像变换求出ω,φ的值,然后求出f的值.
【解析】函数f(x)=sin(ωx+φ)图像上每一点的横坐标缩短为原来的一半,纵坐标不变,则函数变为y=sin(2ωx+φ),再向右平移个单位长度得到的函数为y=sin=sin=sinx,
所以
又因为ω>0,-≤φ<,
可求得ω=,φ=,
所以f(x)=sin,
所以f=sin=sin=.
答案:
【变式训练】将函数y=sinωx(ω>0)的图像向左平移个单位,平移后的图像如图所示,则平移后的图像所对应函数的解析式是 .
【解题指南】先用ω表示出平移后的解析式,再利用图中已知的相位求出ω即可求出解析式.
【解析】函数y=sinωx(ω>0)的图像向左平移个单位得到y=sin,
则πω+=,解得ω=2,
故平移后的图像的解析式为y=sin.
答案:y=sin
三、解答题(每小题10分,共20分)
6.已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的最小正周期为,最小值为-2,图像过,求该函数的解析式.
【解析】因为函数的最小正周期为,
所以T==,即ω=3.
又因为函数的最小值为-2,
所以A=2,
所以函数解析式可写为y=2sin,
又因为函数图像过点,
所以有:2sin=0,
解得φ=kπ-.
因为|φ|<π,
所以φ=或-,
所以,函数解析式为:y=2sin或y=2sin.
7.将函数y=lgx的图像向左平移一个单位长度,可得函数f(x)的图像;将函数y=cos的图像向左平移个单位长度,可得函数g(x)的图像.
(1)在同一直角坐标系中画出函数f(x)和g(x)的图像.
(2)判断方程f(x)=g(x)解的个数.
【解题指南】解答本题(1)利用平移变换法画出两个函数的图像.(2)根据弦函数的“有界性”及lg10=1确定两个函数图像的交点个数,即为方程f(x)=g(x)解的个数.
【解析】函数y=lgx的图像向左平移一个单位长度,可得函数f(x)=lg(x+1)的图像,即图像C1;函数y=cos的图像向左平移个单位长度,可得函数g(x)=cos=cos2x的图像,即图像C2.
(1)画出图像C1和C2如图.
(2)因为f(9)=lg10=1,
所以由图像可知:两个图像共有5个交点.
即方程f(x)=g(x)解的个数为5.
