1.8 函数y=Asin(ωx+ψ)的图像 同步练习2(含答案)
文档属性
| 名称 | 1.8 函数y=Asin(ωx+ψ)的图像 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 173.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-28 14:17:58 | ||
图片预览


文档简介
1.8
函数y=Asin(ωx+ψ)的图像
同步练习
双基达标 限时20分钟
1.要得到函数y=cos(2x+1)的图像,只要将y=cos
2x的图像
( ).
A.左移1个单位
B.右移1个单位
C.左移个单位
D.右移个单位
解析 y=cos(2x+1)=cos
2,∴应将y=cos
2x的图像向左平移个单位.
答案 C
2.函数y=Asin(ωx+φ)+k的图像如图,则它的振幅A与最小正周期T分别是
( ).
A.A=3,T=
B.A=3,T=
C.A=,T=
D.A=,T=
解析 由图像可知最大值为3,最小值为0,故振幅为,半个周期为-=,故周期为π.
答案 D
3.将函数f(x)=sin(ωx+φ)的图像向左平移个单位,若所得图像与原图像重合,则ω的值不可能等于( ).
A.4
B.6
C.8
D.12
解析 由题意得,sin[ω]=sin,则ω=2kπ,k∈Z,∴ω=4k,k∈Z,因为6不是4的整数倍,所以ω的值不可能是6.
答案 B
4.已知函数f(x)=sin(ωx+φ)(ω>0)的图像如图所示,则ω=________.
解析 由图可知,f(x)的周期T=4×,即T=,
故ω===.
答案
5.为得到函数y=cos
x的图像,可以把y=sin
x的图像向右平移φ个单位得到,那么φ的最小正值是________.
解析 y=sin
x=cos=cos向右平移φ个单位后得y=cos,
∴φ+=2kπ,k∈Z,∴φ=2kπ-,k∈Z.
∴φ的最小正值是π.
答案
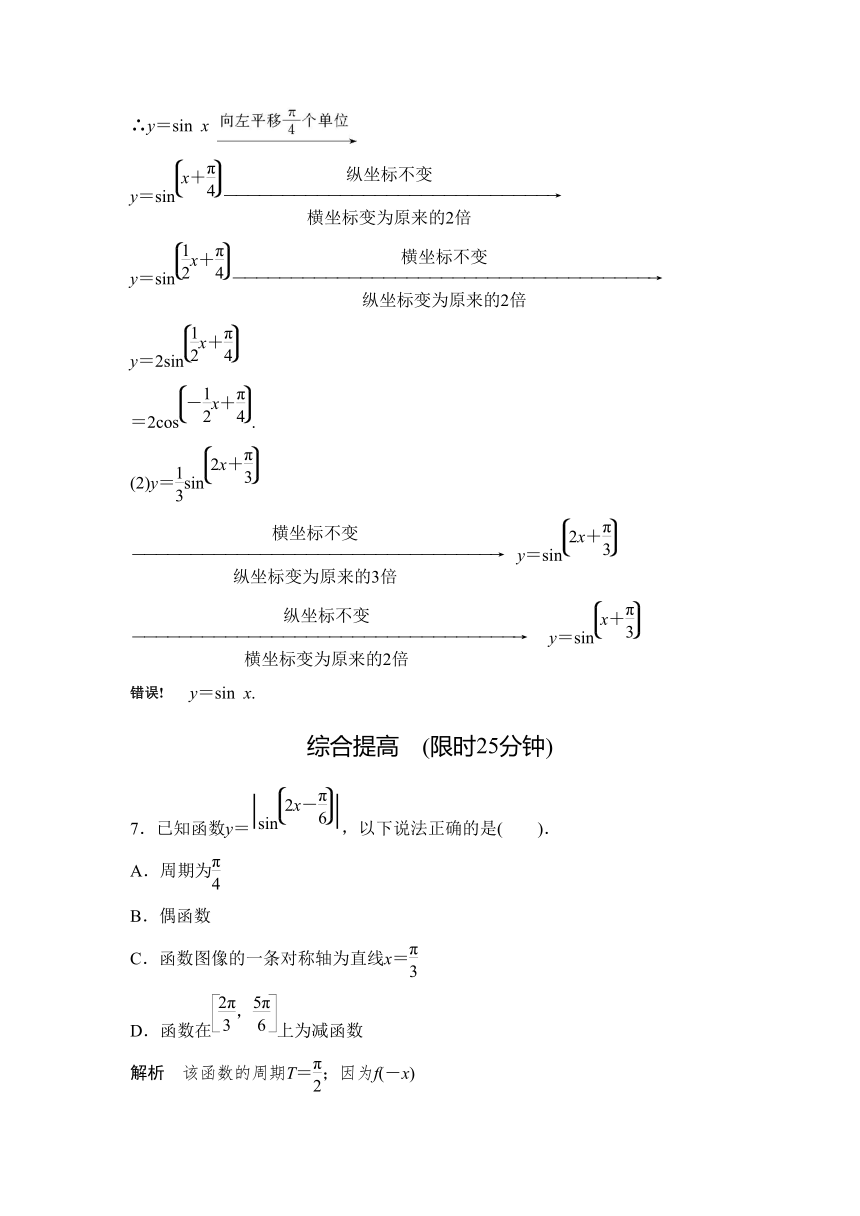
6.(1)如何由y=sin
x的图像得到y=2cos的图像?
(2)如何由y=sin的图像得到y=sin
x的图像
解 (1)∵y=2cos
=2cos
=2cos=2sin,
∴y=sin
x
y=sin
y=sin
y=2sin
=2cos.
(2)y=sin
y=sin
y=sin
y=sin
x.
综合提高 限时25分钟
7.已知函数y=,以下说法正确的是( ).
A.周期为
B.偶函数
C.函数图像的一条对称轴为直线x=
D.函数在上为减函数
解析 该函数的周期T=;因为f(-x)
=
=,
因此它是非奇非偶函数;
函数y=sin在上是减函数.
但y=在
上是增函数,因此只有C正确.
答案 C
8.为了得到函数y=sin,x∈R的图像,只需把函数y=sin
x,x∈R的图像上所有的点( ).
A.向左平移个单位,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
B.向右平移个单位,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
C.向左平移个单位,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移个单位,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
答案 C
9.函数y=-sin的图像与x轴的各个交点中,离原点最近的一点是________.
解析 令-sin=0,
则4x+=kπ,∴x=-,k∈Z
故取k=1时,x=.
∴离原点最近的一点是.
答案
10.已知f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图像如图所示,则f(0)的值是________.
解析 由题图知A=,=-=,T=π,
又T=,∴ω=2,
根据函数图像的对应关系,得2×+φ=2kπ+π
(k∈Z),
∴φ=2kπ+,k∈Z.
令k=0,取φ=,
∴函数解析式为f(x)=sin(2x+),
∴f(0)=sin=.
答案
11.y=Asin(ωx+φ)(A>0,ω>0,|φ|<,x∈R)的部分图像如图所示,求函数表达式.
解 由图像可知,A=4,
=·=6-(-2)=8,
∴ω=,
∴y=4sin.
又(-2,0)在此函数图像上,
∴4sin[×(-2)+φ]=0,
sin=0,∴φ-=kπ,k∈Z,
φ=kπ+,k∈Z,又|φ|<,
∴φ=,∴y=4sin.
12.(创新拓展)已知函数f(x)=Asin,x∈R,A>0,0<φ<,y=f(x)的部分图像,如图所示,P、Q分别为该图像的最高点和最低点,点P的坐标为(1,A).
(1)求f(x)的最小正周期及φ的值;
(2)若点R的坐标为(1,0),∠PRQ=,求A的值.
解 (1)T==6,∵点P(1,A)为函数图像的最高点,
∴×1+φ=+2kπ,k∈Z,∴φ=+2kπ,k∈Z.
又∵0<φ<,∴φ=.
(2)∵Q为函数图像的最低点,P(1,A),=3,
∴Q的坐标为(4,-A).
如图,过点Q作QS⊥OR,交x轴于点S,
则∠QRS=-=.
∵QS=A,RS=4-1=3,
∴tan∠QRS==.
∴tan=,∴A=.
函数y=Asin(ωx+ψ)的图像
同步练习
双基达标 限时20分钟
1.要得到函数y=cos(2x+1)的图像,只要将y=cos
2x的图像
( ).
A.左移1个单位
B.右移1个单位
C.左移个单位
D.右移个单位
解析 y=cos(2x+1)=cos
2,∴应将y=cos
2x的图像向左平移个单位.
答案 C
2.函数y=Asin(ωx+φ)+k的图像如图,则它的振幅A与最小正周期T分别是
( ).
A.A=3,T=
B.A=3,T=
C.A=,T=
D.A=,T=
解析 由图像可知最大值为3,最小值为0,故振幅为,半个周期为-=,故周期为π.
答案 D
3.将函数f(x)=sin(ωx+φ)的图像向左平移个单位,若所得图像与原图像重合,则ω的值不可能等于( ).
A.4
B.6
C.8
D.12
解析 由题意得,sin[ω]=sin,则ω=2kπ,k∈Z,∴ω=4k,k∈Z,因为6不是4的整数倍,所以ω的值不可能是6.
答案 B
4.已知函数f(x)=sin(ωx+φ)(ω>0)的图像如图所示,则ω=________.
解析 由图可知,f(x)的周期T=4×,即T=,
故ω===.
答案
5.为得到函数y=cos
x的图像,可以把y=sin
x的图像向右平移φ个单位得到,那么φ的最小正值是________.
解析 y=sin
x=cos=cos向右平移φ个单位后得y=cos,
∴φ+=2kπ,k∈Z,∴φ=2kπ-,k∈Z.
∴φ的最小正值是π.
答案
6.(1)如何由y=sin
x的图像得到y=2cos的图像?
(2)如何由y=sin的图像得到y=sin
x的图像
解 (1)∵y=2cos
=2cos
=2cos=2sin,
∴y=sin
x
y=sin
y=sin
y=2sin
=2cos.
(2)y=sin
y=sin
y=sin
y=sin
x.
综合提高 限时25分钟
7.已知函数y=,以下说法正确的是( ).
A.周期为
B.偶函数
C.函数图像的一条对称轴为直线x=
D.函数在上为减函数
解析 该函数的周期T=;因为f(-x)
=
=,
因此它是非奇非偶函数;
函数y=sin在上是减函数.
但y=在
上是增函数,因此只有C正确.
答案 C
8.为了得到函数y=sin,x∈R的图像,只需把函数y=sin
x,x∈R的图像上所有的点( ).
A.向左平移个单位,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
B.向右平移个单位,再把所得各点的横坐标缩短到原来的倍(纵坐标不变)
C.向左平移个单位,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移个单位,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
答案 C
9.函数y=-sin的图像与x轴的各个交点中,离原点最近的一点是________.
解析 令-sin=0,
则4x+=kπ,∴x=-,k∈Z
故取k=1时,x=.
∴离原点最近的一点是.
答案
10.已知f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图像如图所示,则f(0)的值是________.
解析 由题图知A=,=-=,T=π,
又T=,∴ω=2,
根据函数图像的对应关系,得2×+φ=2kπ+π
(k∈Z),
∴φ=2kπ+,k∈Z.
令k=0,取φ=,
∴函数解析式为f(x)=sin(2x+),
∴f(0)=sin=.
答案
11.y=Asin(ωx+φ)(A>0,ω>0,|φ|<,x∈R)的部分图像如图所示,求函数表达式.
解 由图像可知,A=4,
=·=6-(-2)=8,
∴ω=,
∴y=4sin.
又(-2,0)在此函数图像上,
∴4sin[×(-2)+φ]=0,
sin=0,∴φ-=kπ,k∈Z,
φ=kπ+,k∈Z,又|φ|<,
∴φ=,∴y=4sin.
12.(创新拓展)已知函数f(x)=Asin,x∈R,A>0,0<φ<,y=f(x)的部分图像,如图所示,P、Q分别为该图像的最高点和最低点,点P的坐标为(1,A).
(1)求f(x)的最小正周期及φ的值;
(2)若点R的坐标为(1,0),∠PRQ=,求A的值.
解 (1)T==6,∵点P(1,A)为函数图像的最高点,
∴×1+φ=+2kπ,k∈Z,∴φ=+2kπ,k∈Z.
又∵0<φ<,∴φ=.
(2)∵Q为函数图像的最低点,P(1,A),=3,
∴Q的坐标为(4,-A).
如图,过点Q作QS⊥OR,交x轴于点S,
则∠QRS=-=.
∵QS=A,RS=4-1=3,
∴tan∠QRS==.
∴tan=,∴A=.
