粤教版物理必修1同步测试:第2章章末复习课 探究匀变速直线运动规律
文档属性
| 名称 | 粤教版物理必修1同步测试:第2章章末复习课 探究匀变速直线运动规律 |

|
|
| 格式 | zip | ||
| 文件大小 | 465.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-12-29 00:00:00 | ||
图片预览



文档简介
第二章章末复习课
【知识体系】
[答案填写] ①静止 ②重力 ③均匀变化 ④大小和方向
主题1 匀变速直线运动规律
的理解和应用
1.公式中各量正负号的确定.
s、a、v0、vt均为矢量,在应用公式时,一般以初速度方向为正方向;凡是与v0方向相同的矢量为正值,相反的矢量为负值.
2.善用逆向思维法.
特别对于末速度为0的匀减速直线运动,倒过来可看成初速度为0的匀加速直线运动,这样公式可以简化(如vt=at,s=at2),初速度为0的比例式也可以应用.
3.注意.
(1)刹车类问题一般先求出刹车时间.
(2)对于有往返的匀变速直线运动(全过程加速度a恒定),可对全过程应用公式vt=v0+at、s=v0t+at2列式求解.
(3)分析题意时要养成画运动过程示意图的习惯.对于多过程问题,要注意前后过程的联系——前段过程的末速度是后一过程的初速度;也要注意寻找位移关系、时间关系.
【典例1】 如图所示,一小物块从静止沿斜面以恒定的加速度下滑,依次通过A、B、C三点,已知AB=12
m,AC=32
m,小物块通过AB、BC所用的时间均为2
s,求:
(1)小物块下滑时的加速度;
(2)小物块通过A、B、C三点时的速度.
解:解法一 (1)设物块下滑的加速度为a,则sBC-sAB=at2,所以a==
m/s2=2
m/s2.
(2)vB==
m/s=8
m/s.
解法二 由vt=v0+at得vA=vB-at=(8-2×2)
m/s=4
m/s,
vC=vB+at=(8+2×2)
m/s=12
m/s.
由s=v0t+at2知:
AB段:12=vA×2+a×22,①
AC段:32=vA×4+a×42,②
①②联立得vA=4
m/s,a=2
m/s2.
所以vB=vA+at=8
m/s,vC=vA+a·2t=12
m/s.
解法三 vB==8
m/s,由sBC=vBt+at2,
即20=8×2+a×22,得a=2
m/s2.
由vt=v0+at知vA=vB-at=4
m/s,vC=vB+at=
12
m/s.
答案:(1)2
m/s2 (2)vA=4
m/s vB=8
m/s
vC=12
m/s
针对训练
1.汽车以20
m/s的速度做匀减速直线运动,刹车时的加速度为5
m/s2,那么开始刹车后2
s与开始刹车后6
s汽车通过的位移之比为( )
A.1∶4
B.3∶5
C.3∶4
D.5∶9
解析:汽车的停车时间t0==4
s,
刹车后2
s的位移为s1=v0·t1-at=30
m.
刹车后6
s的位移等于4
s的位移,
刹车后4
s的位移可看作反向匀加速直线运动,
s2=at=40
m,另解:s2=eq
\f(v,2a)=40
m.
答案:C
主题2 运动图象问题
1.“六看”识图象.
首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”.
(1)“轴”:纵、横轴所表示的物理量,特别要注意纵轴是s,还是v.
(2)“线”:从线反映运动性质,如st图象为水平直线表示匀速运动,vt图象为水平直线表示匀速运动,vt图象为倾斜直线表示匀变速运动.
(3)“斜率”:st图象斜率表示速度;vt图象斜率表示加速度.
(4)“面”即“面积”:主要看纵、横轴量的乘积有无意义.如st图象面积无意义,vt图象与t轴所围面积表示位移.
(5)“截距”:初始条件、初始位置s0或初速度v0.
(6)“特殊值”:如交点,st图象交点表示相遇,vt图象交点表示速度相等(不表示相遇).
2.如下是s-t图象和v-t图象的比较.
s-t图
v-t图
①表示物体做匀速直线运动(斜率大小表示速度的大小)②表示物体静止③表示物体反向匀速直线运动(斜率大小表示速度的大小)④交点的纵坐标表示三个运动质点相遇时的位移⑤t1时刻物体的位移为s1
①表示物体做匀加速直线运动(斜率大小表示加速度的大小)
②表示物体做匀速直线运动③表示物体做匀减速直线运动(斜率大小表示加速度的大小)④交点的纵坐标表示三个运动质点在同一时刻的共同速度⑤t1时刻物体的速度为v1(阴影部分面积表示质点在t1时间内的位移)
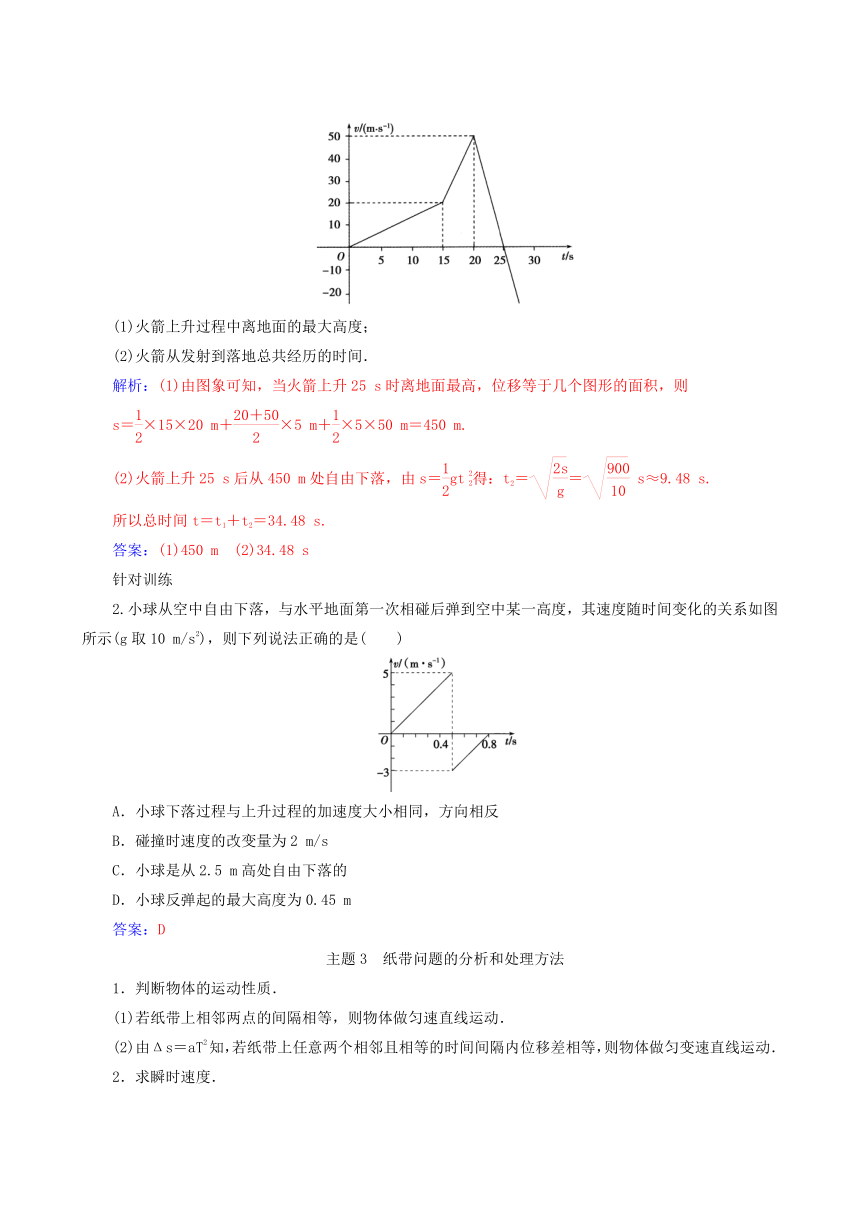
【典例2】 一枚火箭由地面竖直向上发射,但由于发动机故障而发射失败,其速度—时间图象如图所示,根据图象求(已知=3.16,g取10
m/s2):
(1)火箭上升过程中离地面的最大高度;
(2)火箭从发射到落地总共经历的时间.
解析:(1)由图象可知,当火箭上升25
s时离地面最高,位移等于几个图形的面积,则
s=×15×20
m+×5
m+×5×50
m=450
m.
(2)火箭上升25
s后从450
m处自由下落,由s=gt得:t2==
s≈9.48
s.
所以总时间t=t1+t2=34.48
s.
答案:(1)450
m (2)34.48
s
针对训练
2.小球从空中自由下落,与水平地面第一次相碰后弹到空中某一高度,其速度随时间变化的关系如图所示(g取10
m/s2),则下列说法正确的是( )
A.小球下落过程与上升过程的加速度大小相同,方向相反
B.碰撞时速度的改变量为2
m/s
C.小球是从2.5
m高处自由下落的
D.小球反弹起的最大高度为0.45
m
答案:D
主题3 纸带问题的分析和处理方法
1.判断物体的运动性质.
(1)若纸带上相邻两点的间隔相等,则物体做匀速直线运动.
(2)由Δs=aT2知,若纸带上任意两个相邻且相等的时间间隔内位移差相等,则物体做匀变速直线运动.
2.求瞬时速度.
在匀变速直线运动中,某段时间内的平均速度等于该段时间中间时刻的瞬时速度:vn=.
3.求加速度.
(1)逐差法.
如图所示,纸带上有六个连续相等的时间T内的位移s1、s2、s3、s4、s5、s6.
则a=
由此可以看出,各段位移都用上了,有效地减小了偶然误差,所以利用纸带计算加速度时,可采用逐差法.
(2)图象法.
先求出各时刻的瞬时速度v1、v2、v3、…、vn,然后作vt图象,求出该vt图线的斜率k,则k=a.这种方法的优点是可以舍掉一些偶然误差较大的测量值,因此求得值的偶然误差较小.
【典例3】 在测定匀变速直线运动的加速度的实验中,得到一条如图所示的纸带,按时间顺序取0、1、2、3、4、5、6共七个计数点,每相邻两个计数点间各有四个打点的点未画出,用刻度尺测得1、2、3、…、6各点到0点的距离分别为8.69
cm,15.99
cm,21.87
cm,26.35
cm,29.45
cm,31.17
cm,打点计时器每隔0.02
s打一次点.求:
(1)小车的加速度;
(2)打计数点3时小车的速度.
解析:(1)由纸带的数据可知,小车在连续相等的时间T=0.1
s内的位移分别为s1=8.69
cm,s2=7.30
cm,s3=5.88
cm,s4=4.48
cm,s5=3.10
cm,s6=1.72
cm.
由逐差法可得小车的加速度为:
a==
×10-2m/s2≈
-1.397
m/s2.
(2)打计数点3时小车的速度v3=,
代入数据解得v3=0.518
m/s.
答案:(1)-1.397
m/s2 (2)0.518
m/s
针对训练
3.如图所示是某同学在“研究匀变速直线运动”的实验中获得的一条纸带.
(1)已知打点计时器电源频率为50
Hz,则纸带上打相邻两点的时间间隔为________
s.
(2)A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图中求出C点对应的速度是________
m/s,运动的加速度是________
m/s2(计算结果保留三位有效数字).
答案:(1)0.02 (2)0.210 0.600
统揽考情
本章知识核心是物体的匀变速直线运动问题,高考对本章考查的内容主要有:①匀变速直线运动的规律及运动图象问题;②行车安全问题.
真题例析
(2015·广东卷)甲、乙两人同时同地出发骑自行车做直线运动,前1小时内的位移—时间图象如图所示.下列表述正确的是( )
A.0.2~0.5小时内,甲的加速度比乙的大
B.0.2~0.5小时内,甲的速度比乙的大
C.0.6~0.8小时内,甲的位移比乙的小
D.0.8小时内,甲、乙骑行的路程相等
解析:题图为s-t图象,图象的斜率表示速度.根据图象可知0.2~0.5小时内,甲、乙都做匀速直线运动,加速度都为0,甲的斜率比乙大,所以甲的速度大于乙的速度,A错误,B正确;0.6~0.8小时内,甲的位移是-5
m,乙的位移是-3
m,C错误;0.8小时内,甲、乙的位移相同,但是路程不一样,D错误.
答案:B
针对训练
竖直升空的火箭,其速度—时间图象如图所示,由图可知以下说法正确的是( )
A.火箭在40
s时速度方向发生变化
B.火箭上升的最大高度为48
000
m
C.火箭经过120
s落回地面
D.火箭经过40
s到达最高点
解析:由速度—时间图象知,火箭前40
s向上匀加速运动,40~120
s内向上做匀减速直线运动,所以A、C、D错.上升的最大高度h=×800×120
m=48
000
m,B对.
答案:B
1.(多选)物体运动的初速度为6
m/s,经过10
s速度的大小变为20
m/s,则加速度大小可能是( )
A.0.8
m/s2
B.1.4
m/s2
C.2.0
m/s2
D.2.6
m/s2
解析:经10
s后物体的速度大小变为20
m/s,速度的方向有两种可能,与初速度方向相同或相反,由加速度的定义式a=可知,B、D正确.
答案:BD
2.(多选)一个物体以v0=8
m/s的初速度沿光滑斜面向上滑,加速度的大小为2
m/s2,冲上最高点之后,又以相同的加速度往回运动.则( )
A.1
s末的速度大小为6
m/s
B.3
s末的速度为零
C.2
s内的位移大小是12
m
D.5
s内的位移是16
m
解析:由t上==4
s,即物体冲上最高点的时间为4
s,又根据vt=v0+at得物体1
s末的速度为6
m/s,A对,B错.根据s=v0t+at2,物体2
s内的位移是12
m,4
s内的位移是16
m,第5
s内,物体沿斜面返回,仍可用上述公式求得5
s的位移是15
m,亦可求第5
s内下滑1
m,得5
s内位移为15
m,所以C对,D错.
答案:AC
3.(多选)汽车B在平直公路上行驶,发现前方沿同方向行驶的汽车A速度较小,为了避免相撞,距A车25
m处B车制动,此后它们的v-t图象如图所示,则( )
A.汽车B的加速度大小为3.75
m/s2
B.汽车A、B在t=4
s时的速度相同
C.汽车A、B在0~4
s内的位移相同
D.汽车A、B两车不会相撞
解析:汽车B的加速度大小为a=
m/s2=2.5
m/s2,故A错误;根据图象知,t=4
s时汽车A、B的速度相同,故B正确;在速度—时间图象中,图线与时间轴围成的面积表示物体的位移,故C错误;当它们速度相等时,汽车A的位移sA=5×4
m=20
m,汽车B的位移sB=×(15+5)×4
m=40
m,因为sBm,故汽车B追不上汽车A,即不会相撞,D正确.
答案:BD
4.在“测定匀变速直线运动加速度”的实验中得到一条纸带,纸带上每相邻的两计数点间都有4个点未画出,按时间顺序取0、1、2、3、4、5、6共7个计数点,测出1、2、3、4、5、6点到0点的距离,如图所示(单位:cm).由纸带数据计算可得:(1)计数点4所代表时刻的瞬时速度大小v4=________
m/s;(2)小车的加速度大小为________
m/s2(保留2位有效数字).
解析:(1)相邻计数点之间都还有4个点未画出,说明相邻计数点之间的时间间隔是0.1
s.由全程的平均速度等于中间时刻的瞬时速度得:
v4=
m/s≈0.41
m/s.
(2)由Δs=aT2得:
a=×10-2
m/s2≈0.76
m/s2.
答案:(1)0.41 (2)0.76
5.一辆长途客车正在以v=16
m/s的速度匀速行驶,突然,司机看见车的正前方s=36
m处有一只小狗(如图甲),司机立即采取制动措施.从司机看见小狗到长途客车开始做匀减速直线运动的时间间隔Δt=0.5
s.若从司机看见小狗开始计时(t=0),该长途客车的速度—时间图象如图乙所示.求:
(1)长途客车在Δt时间内前进的距离;
(2)长途客车从司机发现小狗至停止运动的这段时间内前进的距离;
(3)根据你的计算结果,判断小狗是否安全.
解析:(1)长途客车在司机的反应时间内前进的距离:
s1=vΔt=16×0.5
m=8
m.
(2)从司机发现小狗至停止的时间内长途客车前进的距离:s2=s1+=40
m.
(3)因为s2>s,所以小狗不安全.
答案:(1)8
m (2)40
m (3)小狗不安全
【知识体系】
[答案填写] ①静止 ②重力 ③均匀变化 ④大小和方向
主题1 匀变速直线运动规律
的理解和应用
1.公式中各量正负号的确定.
s、a、v0、vt均为矢量,在应用公式时,一般以初速度方向为正方向;凡是与v0方向相同的矢量为正值,相反的矢量为负值.
2.善用逆向思维法.
特别对于末速度为0的匀减速直线运动,倒过来可看成初速度为0的匀加速直线运动,这样公式可以简化(如vt=at,s=at2),初速度为0的比例式也可以应用.
3.注意.
(1)刹车类问题一般先求出刹车时间.
(2)对于有往返的匀变速直线运动(全过程加速度a恒定),可对全过程应用公式vt=v0+at、s=v0t+at2列式求解.
(3)分析题意时要养成画运动过程示意图的习惯.对于多过程问题,要注意前后过程的联系——前段过程的末速度是后一过程的初速度;也要注意寻找位移关系、时间关系.
【典例1】 如图所示,一小物块从静止沿斜面以恒定的加速度下滑,依次通过A、B、C三点,已知AB=12
m,AC=32
m,小物块通过AB、BC所用的时间均为2
s,求:
(1)小物块下滑时的加速度;
(2)小物块通过A、B、C三点时的速度.
解:解法一 (1)设物块下滑的加速度为a,则sBC-sAB=at2,所以a==
m/s2=2
m/s2.
(2)vB==
m/s=8
m/s.
解法二 由vt=v0+at得vA=vB-at=(8-2×2)
m/s=4
m/s,
vC=vB+at=(8+2×2)
m/s=12
m/s.
由s=v0t+at2知:
AB段:12=vA×2+a×22,①
AC段:32=vA×4+a×42,②
①②联立得vA=4
m/s,a=2
m/s2.
所以vB=vA+at=8
m/s,vC=vA+a·2t=12
m/s.
解法三 vB==8
m/s,由sBC=vBt+at2,
即20=8×2+a×22,得a=2
m/s2.
由vt=v0+at知vA=vB-at=4
m/s,vC=vB+at=
12
m/s.
答案:(1)2
m/s2 (2)vA=4
m/s vB=8
m/s
vC=12
m/s
针对训练
1.汽车以20
m/s的速度做匀减速直线运动,刹车时的加速度为5
m/s2,那么开始刹车后2
s与开始刹车后6
s汽车通过的位移之比为( )
A.1∶4
B.3∶5
C.3∶4
D.5∶9
解析:汽车的停车时间t0==4
s,
刹车后2
s的位移为s1=v0·t1-at=30
m.
刹车后6
s的位移等于4
s的位移,
刹车后4
s的位移可看作反向匀加速直线运动,
s2=at=40
m,另解:s2=eq
\f(v,2a)=40
m.
答案:C
主题2 运动图象问题
1.“六看”识图象.
首先要学会识图.识图就是通过“看”寻找规律及解题的突破口.为方便记忆,这里总结为六看:一看“轴”,二看“线”,三看“斜率”,四看“面”,五看“截距”,六看“特殊值”.
(1)“轴”:纵、横轴所表示的物理量,特别要注意纵轴是s,还是v.
(2)“线”:从线反映运动性质,如st图象为水平直线表示匀速运动,vt图象为水平直线表示匀速运动,vt图象为倾斜直线表示匀变速运动.
(3)“斜率”:st图象斜率表示速度;vt图象斜率表示加速度.
(4)“面”即“面积”:主要看纵、横轴量的乘积有无意义.如st图象面积无意义,vt图象与t轴所围面积表示位移.
(5)“截距”:初始条件、初始位置s0或初速度v0.
(6)“特殊值”:如交点,st图象交点表示相遇,vt图象交点表示速度相等(不表示相遇).
2.如下是s-t图象和v-t图象的比较.
s-t图
v-t图
①表示物体做匀速直线运动(斜率大小表示速度的大小)②表示物体静止③表示物体反向匀速直线运动(斜率大小表示速度的大小)④交点的纵坐标表示三个运动质点相遇时的位移⑤t1时刻物体的位移为s1
①表示物体做匀加速直线运动(斜率大小表示加速度的大小)
②表示物体做匀速直线运动③表示物体做匀减速直线运动(斜率大小表示加速度的大小)④交点的纵坐标表示三个运动质点在同一时刻的共同速度⑤t1时刻物体的速度为v1(阴影部分面积表示质点在t1时间内的位移)
【典例2】 一枚火箭由地面竖直向上发射,但由于发动机故障而发射失败,其速度—时间图象如图所示,根据图象求(已知=3.16,g取10
m/s2):
(1)火箭上升过程中离地面的最大高度;
(2)火箭从发射到落地总共经历的时间.
解析:(1)由图象可知,当火箭上升25
s时离地面最高,位移等于几个图形的面积,则
s=×15×20
m+×5
m+×5×50
m=450
m.
(2)火箭上升25
s后从450
m处自由下落,由s=gt得:t2==
s≈9.48
s.
所以总时间t=t1+t2=34.48
s.
答案:(1)450
m (2)34.48
s
针对训练
2.小球从空中自由下落,与水平地面第一次相碰后弹到空中某一高度,其速度随时间变化的关系如图所示(g取10
m/s2),则下列说法正确的是( )
A.小球下落过程与上升过程的加速度大小相同,方向相反
B.碰撞时速度的改变量为2
m/s
C.小球是从2.5
m高处自由下落的
D.小球反弹起的最大高度为0.45
m
答案:D
主题3 纸带问题的分析和处理方法
1.判断物体的运动性质.
(1)若纸带上相邻两点的间隔相等,则物体做匀速直线运动.
(2)由Δs=aT2知,若纸带上任意两个相邻且相等的时间间隔内位移差相等,则物体做匀变速直线运动.
2.求瞬时速度.
在匀变速直线运动中,某段时间内的平均速度等于该段时间中间时刻的瞬时速度:vn=.
3.求加速度.
(1)逐差法.
如图所示,纸带上有六个连续相等的时间T内的位移s1、s2、s3、s4、s5、s6.
则a=
由此可以看出,各段位移都用上了,有效地减小了偶然误差,所以利用纸带计算加速度时,可采用逐差法.
(2)图象法.
先求出各时刻的瞬时速度v1、v2、v3、…、vn,然后作vt图象,求出该vt图线的斜率k,则k=a.这种方法的优点是可以舍掉一些偶然误差较大的测量值,因此求得值的偶然误差较小.
【典例3】 在测定匀变速直线运动的加速度的实验中,得到一条如图所示的纸带,按时间顺序取0、1、2、3、4、5、6共七个计数点,每相邻两个计数点间各有四个打点的点未画出,用刻度尺测得1、2、3、…、6各点到0点的距离分别为8.69
cm,15.99
cm,21.87
cm,26.35
cm,29.45
cm,31.17
cm,打点计时器每隔0.02
s打一次点.求:
(1)小车的加速度;
(2)打计数点3时小车的速度.
解析:(1)由纸带的数据可知,小车在连续相等的时间T=0.1
s内的位移分别为s1=8.69
cm,s2=7.30
cm,s3=5.88
cm,s4=4.48
cm,s5=3.10
cm,s6=1.72
cm.
由逐差法可得小车的加速度为:
a==
×10-2m/s2≈
-1.397
m/s2.
(2)打计数点3时小车的速度v3=,
代入数据解得v3=0.518
m/s.
答案:(1)-1.397
m/s2 (2)0.518
m/s
针对训练
3.如图所示是某同学在“研究匀变速直线运动”的实验中获得的一条纸带.
(1)已知打点计时器电源频率为50
Hz,则纸带上打相邻两点的时间间隔为________
s.
(2)A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图中求出C点对应的速度是________
m/s,运动的加速度是________
m/s2(计算结果保留三位有效数字).
答案:(1)0.02 (2)0.210 0.600
统揽考情
本章知识核心是物体的匀变速直线运动问题,高考对本章考查的内容主要有:①匀变速直线运动的规律及运动图象问题;②行车安全问题.
真题例析
(2015·广东卷)甲、乙两人同时同地出发骑自行车做直线运动,前1小时内的位移—时间图象如图所示.下列表述正确的是( )
A.0.2~0.5小时内,甲的加速度比乙的大
B.0.2~0.5小时内,甲的速度比乙的大
C.0.6~0.8小时内,甲的位移比乙的小
D.0.8小时内,甲、乙骑行的路程相等
解析:题图为s-t图象,图象的斜率表示速度.根据图象可知0.2~0.5小时内,甲、乙都做匀速直线运动,加速度都为0,甲的斜率比乙大,所以甲的速度大于乙的速度,A错误,B正确;0.6~0.8小时内,甲的位移是-5
m,乙的位移是-3
m,C错误;0.8小时内,甲、乙的位移相同,但是路程不一样,D错误.
答案:B
针对训练
竖直升空的火箭,其速度—时间图象如图所示,由图可知以下说法正确的是( )
A.火箭在40
s时速度方向发生变化
B.火箭上升的最大高度为48
000
m
C.火箭经过120
s落回地面
D.火箭经过40
s到达最高点
解析:由速度—时间图象知,火箭前40
s向上匀加速运动,40~120
s内向上做匀减速直线运动,所以A、C、D错.上升的最大高度h=×800×120
m=48
000
m,B对.
答案:B
1.(多选)物体运动的初速度为6
m/s,经过10
s速度的大小变为20
m/s,则加速度大小可能是( )
A.0.8
m/s2
B.1.4
m/s2
C.2.0
m/s2
D.2.6
m/s2
解析:经10
s后物体的速度大小变为20
m/s,速度的方向有两种可能,与初速度方向相同或相反,由加速度的定义式a=可知,B、D正确.
答案:BD
2.(多选)一个物体以v0=8
m/s的初速度沿光滑斜面向上滑,加速度的大小为2
m/s2,冲上最高点之后,又以相同的加速度往回运动.则( )
A.1
s末的速度大小为6
m/s
B.3
s末的速度为零
C.2
s内的位移大小是12
m
D.5
s内的位移是16
m
解析:由t上==4
s,即物体冲上最高点的时间为4
s,又根据vt=v0+at得物体1
s末的速度为6
m/s,A对,B错.根据s=v0t+at2,物体2
s内的位移是12
m,4
s内的位移是16
m,第5
s内,物体沿斜面返回,仍可用上述公式求得5
s的位移是15
m,亦可求第5
s内下滑1
m,得5
s内位移为15
m,所以C对,D错.
答案:AC
3.(多选)汽车B在平直公路上行驶,发现前方沿同方向行驶的汽车A速度较小,为了避免相撞,距A车25
m处B车制动,此后它们的v-t图象如图所示,则( )
A.汽车B的加速度大小为3.75
m/s2
B.汽车A、B在t=4
s时的速度相同
C.汽车A、B在0~4
s内的位移相同
D.汽车A、B两车不会相撞
解析:汽车B的加速度大小为a=
m/s2=2.5
m/s2,故A错误;根据图象知,t=4
s时汽车A、B的速度相同,故B正确;在速度—时间图象中,图线与时间轴围成的面积表示物体的位移,故C错误;当它们速度相等时,汽车A的位移sA=5×4
m=20
m,汽车B的位移sB=×(15+5)×4
m=40
m,因为sB
答案:BD
4.在“测定匀变速直线运动加速度”的实验中得到一条纸带,纸带上每相邻的两计数点间都有4个点未画出,按时间顺序取0、1、2、3、4、5、6共7个计数点,测出1、2、3、4、5、6点到0点的距离,如图所示(单位:cm).由纸带数据计算可得:(1)计数点4所代表时刻的瞬时速度大小v4=________
m/s;(2)小车的加速度大小为________
m/s2(保留2位有效数字).
解析:(1)相邻计数点之间都还有4个点未画出,说明相邻计数点之间的时间间隔是0.1
s.由全程的平均速度等于中间时刻的瞬时速度得:
v4=
m/s≈0.41
m/s.
(2)由Δs=aT2得:
a=×10-2
m/s2≈0.76
m/s2.
答案:(1)0.41 (2)0.76
5.一辆长途客车正在以v=16
m/s的速度匀速行驶,突然,司机看见车的正前方s=36
m处有一只小狗(如图甲),司机立即采取制动措施.从司机看见小狗到长途客车开始做匀减速直线运动的时间间隔Δt=0.5
s.若从司机看见小狗开始计时(t=0),该长途客车的速度—时间图象如图乙所示.求:
(1)长途客车在Δt时间内前进的距离;
(2)长途客车从司机发现小狗至停止运动的这段时间内前进的距离;
(3)根据你的计算结果,判断小狗是否安全.
解析:(1)长途客车在司机的反应时间内前进的距离:
s1=vΔt=16×0.5
m=8
m.
(2)从司机发现小狗至停止的时间内长途客车前进的距离:s2=s1+=40
m.
(3)因为s2>s,所以小狗不安全.
答案:(1)8
m (2)40
m (3)小狗不安全
同课章节目录
- 第一章 运动的描述
- 第一节 认识运动
- 第二节 时间 位移
- 第三节 记录物体的运动信息
- 第四节 物体运动的速度
- 第五节 速度变化的快慢 加速度
- 第六节 用图象描述直线运动
- 第二章 探究匀变速直线运动规律
- 第一节 探究自由落体运动
- 第二节 自由落体运动规律
- 第三节 从自由落体到匀变速直线运动
- 第四节 匀变速直线运动与汽车行驶安全
- 第三章 研究物体间的相互作用
- 第一节 探究形变与弹力的关系
- 第二节 研究摩擦力
- 第三节 力的等效和替代
- 第四节 力的合成与分解
- 第五节 共点力的平衡条件
- 第六节 作用力与反作用力
- 第四章 力与运动
- 第一节 伽利略的理想实验与牛顿第一定律
- 第二节 影响加速度的因素
- 第三节 探究物体运动与受力的关系
- 第四节 牛顿第二定律
- 第五节 牛顿第二定律的应用
- 第六节 超重和失重
- 第七节 力学单位
