山东省济宁市微山一中2016-2017学年高二(上)入学数学试卷(文科)(解析版)
文档属性
| 名称 | 山东省济宁市微山一中2016-2017学年高二(上)入学数学试卷(文科)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-30 00:00:00 | ||
图片预览




文档简介
2016-2017学年山东省济宁市微山一中高二(上)入学数学试卷(文科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.sin(﹣π)的值是( )
A.
B.
C.﹣
D.﹣
2.已知ABCD为平行四边形,若向量,,则向量为( )
A.﹣
B.
+
C.﹣
D.﹣﹣
3.函数y=sin2x是( )
A.周期为π的奇函数
B.周期为π的偶函数
C.周期为2π的奇函数
D.周期为2π的偶函数
4.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( )
A.
B.
C.
D.
5.已知sinα=,并且α是第二象限的角,那么tanα的值等于( )
A.﹣
B.﹣
C.
D.
6.如图所示,随机在图中撒一把豆子,则它落到阴影部分的概率是( )
A.
B.
C.
D.
7.函数y=cos(2x+)的图象的一条对称轴方程是( )
A.x=﹣
B.x=﹣
C.x=
D.x=π
8.直线4x+3y=40与圆x2+y2=100的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
9.一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是( )
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
10.某班学生在一次数学考试中各分数段以及人数的成绩分布为:[0,80),2人;[80,90),6人;[90,100),4人;[100,110),8人;[110,120),12人;[120,130),5人;[130,140),6人;[140,150),2人.那么分数在[100,130)中的频数以及频率分别为( )
A.25,0.56
B.20,0.56
C.25,0.50
D.13,0.29
11.要得到函数y=cosx的图象,只需将函数y=sin(2x+)的图象上所有的点的( )
A.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度
12.函数f(x)=若f(1)+f(a)=2,则a的所有可能值为( )
A.1
B.﹣
C.1,﹣
D.1,
二、填空题:本大题共4小题,每小题4分,共20分.
13.圆x2﹣4x+y2﹣21=0的半径为 .
14.已知向量,向量=(x,3),且,则x= .
15.某中学高一、高二、高三学生人数之比依次为2:3:5,现用分层抽样的方法抽出一个样本空量为n的样本,样本中高三学生有150人,那么n的值等于 .
16.如图给出的是计算+++…+的值的一个流程图,其中判断框内应填入的条件是
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤
17.已知向量,的坐标分别是(﹣1,2),(3,﹣5),求+,﹣,3,2+3的坐标.
18.已知||=4,||=,
=6,求
(1)(﹣) ;
(2)求|+|.
19.求经过直线2x+3y+1=0与x﹣3y+4=0的交点,且与直线3x+4y﹣7=0垂直的直线的方程.
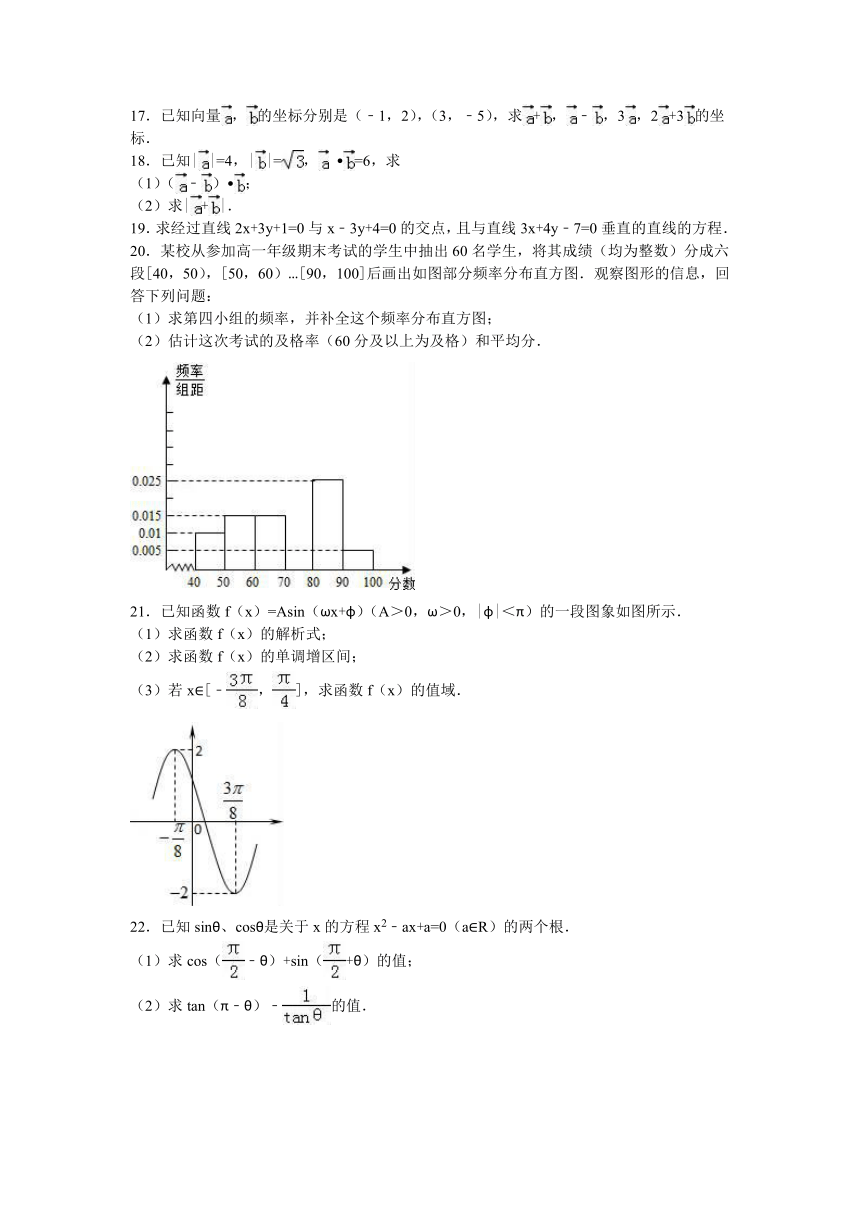
20.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[﹣,],求函数f(x)的值域.
22.已知sinθ、cosθ是关于x的方程x2﹣ax+a=0(a∈R)的两个根.
(1)求cos(﹣θ)+sin(+θ)的值;
(2)求tan(π﹣θ)﹣的值.?
2016-2017学年山东省济宁市微山一中高二(上)入学数学试卷(文科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.sin(﹣π)的值是( )
A.
B.
C.﹣
D.﹣
【考点】三角函数的化简求值.
【分析】利用诱导公式以及特殊角的三角函数化简求值即可.
【解答】解:sin(﹣π)=﹣sin=﹣.
故选:D.
2.已知ABCD为平行四边形,若向量,,则向量为( )
A.﹣
B.
+
C.﹣
D.﹣﹣
【考点】平面向量的基本定理及其意义.
【分析】如图所示,利用向量的减法法则即可得出.
【解答】解:如图所示,
由向量的减法法则可得:
==.
故选C.
3.函数y=sin2x是( )
A.周期为π的奇函数
B.周期为π的偶函数
C.周期为2π的奇函数
D.周期为2π的偶函数
【考点】三角函数的周期性及其求法.
【分析】利用正弦函数的奇偶性与周期性即可得到答案.
【解答】解:∵y=f(x)=sin2x,
∴T==π,
又f(﹣x)=sin2(﹣x)=﹣sin2x=﹣f(x),
∴y=sin2x是奇函数,
∴y=sin2x是周期为π的奇函数,
故选:A.
4.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】简化模型,只考虑第999次出现的结果,有两种结果,第999次出现正面朝上只有一种结果,即可求
【解答】解:抛掷一枚质地均匀的硬币,只考虑第999次,有两种结果:正面朝上,反面朝上,每中结果等可能出现,故所求概率为
故选D
5.已知sinα=,并且α是第二象限的角,那么tanα的值等于( )
A.﹣
B.﹣
C.
D.
【考点】同角三角函数基本关系的运用.
【分析】由角的正弦值和角所在的象限,求出角的余弦值,然后,正弦值除以余弦值得正切值.
【解答】解:∵sinα=且α是第二象限的角,
∴,
∴,
故选A
6.如图所示,随机在图中撒一把豆子,则它落到阴影部分的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】由题意知本题是一个几何概型,试验包含的所有事件对应的图形是整个圆.而满足条件的事件对应的是阴影部分,根据几何概型概率公式得到结果.
【解答】解:由题意知本题是一个几何概型,
试验包含的所有事件是对应的图形是整个圆,
而满足条件的事件是事件对应的是阴影部分,
由几何概型概率公式得到P==.
故选C.
7.函数y=cos(2x+)的图象的一条对称轴方程是( )
A.x=﹣
B.x=﹣
C.x=
D.x=π
【考点】余弦函数的对称性.
【分析】根据三角函数的图象,三角函数的函数值取最值时,对称轴的x取值.
【解答】解:此函数的对称轴方程为,当k=0时,.
故选B.
8.直线4x+3y=40与圆x2+y2=100的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
【考点】直线与圆的位置关系.
【分析】由圆的标准方程,求得圆心与半径,根据圆心到直线的距离与半径的大小关系,确定直线与圆的位置关系.
【解答】解:圆x2+y2=100的圆心为原点(0,0),半径r=10.
由圆心(0,0)到直线4x+3y=40的距离d==8,
由d<r,
∴直线4x+3y=40与圆x2+y2=100相交,
故选:A.
9.一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是( )
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
【考点】互斥事件与对立事件.
【分析】直接根据对立事件的定义,可得事件“至少有一次中靶”的对立事件,从而得出结论.
【解答】解:根据对立事件的定义可得,事件“至少有一次中靶”的对立事件是:两次都不中靶,
故选D.
10.某班学生在一次数学考试中各分数段以及人数的成绩分布为:[0,80),2人;[80,90),6人;[90,100),4人;[100,110),8人;[110,120),12人;[120,130),5人;[130,140),6人;[140,150),2人.那么分数在[100,130)中的频数以及频率分别为( )
A.25,0.56
B.20,0.56
C.25,0.50
D.13,0.29
【考点】频率分布表;频率分布直方图.
【分析】频数与总数的比为频率,由此能求出结果.
【解答】解:分数在[100,130)的频数为:8+12+5=25,
样本容量为2+6+4+8+12+5+6+2=45,
所求的频率值为:≈0.56.
故选:A.
11.要得到函数y=cosx的图象,只需将函数y=sin(2x+)的图象上所有的点的( )
A.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】根据题意,有y=sin(2x+)=cos(﹣2x﹣)=,再由变换规律可得答案.
【解答】解:∵y=sin(2x+)==
答案为C
故选C
12.函数f(x)=若f(1)+f(a)=2,则a的所有可能值为( )
A.1
B.﹣
C.1,﹣
D.1,
【考点】分段函数的解析式求法及其图象的作法.
【分析】由分段函数的解析式容易得出,f(1)=e1﹣1=1,∴f(a)=1,然后在每一段上求函数的值为1时对应的a的值即可.
【解答】解:由题意知,当﹣1<x<0时,f(x)=sin(πx2);
当x≥0时,f(x)=ex﹣1;
∴f(1)=e1﹣1=1.
若f(1)+f(a)=2,则f(a)=1;
当a≥0时,ea﹣1=1,∴a=1;
当﹣1<a<0时,sin(πx2)=1,
∴,x=(不满足条件,舍去),或x=.
所以a的所有可能值为:1,.
故答案为:C
二、填空题:本大题共4小题,每小题4分,共20分.
13.圆x2﹣4x+y2﹣21=0的半径为 5 .
【考点】圆的一般方程.
【分析】将一般方程化为标准方程,即可得到圆的半径.
【解答】解:圆x2﹣4x+y2﹣21=0化为标准方程为(x﹣2)2+y2=25
∴圆的半径为5
故答案为:5
14.已知向量,向量=(x,3),且,则x= 6 .
【考点】平面向量共线(平行)的坐标表示.
【分析】根据所给的两个向量的坐标和两个向量平行的充要条件,得到关于x的方程,解方程即可得到要求的x的值.
【解答】解:因为向量,向量=(x,3),且,根据向量共线的充要条件得4×3=2x,x=6
故答案为:6.
15.某中学高一、高二、高三学生人数之比依次为2:3:5,现用分层抽样的方法抽出一个样本空量为n的样本,样本中高三学生有150人,那么n的值等于 300 .
【考点】分层抽样方法.
【分析】令高三学生在所有学生中所占的比例等于抽到的高三学生与样本容量的比,列出方程,求出n的值.
【解答】解:∵高一、高二、高三学生人数之比依次为2:3:5
∴
解得n=300
故答案为:300
16.如图给出的是计算+++…+的值的一个流程图,其中判断框内应填入的条件是 “i≥11”或“i>10”
【考点】程序框图.
【分析】由本程序的功能是计算+++…+的值,由S=S+,故我们知道最后一次进行循环时的条件为i=10,当i≥11应退出循环输出S的值,由此不难得到判断框中的条件.
【解答】解:∵S=+++…+
并由流程图中S=S+
故循环的初值为1
终值为10、步长为1
故经过10次循环才能算出S=+++…+的值,
故i≤10,应不满足条件,继续循环
∴当i≥11,应满足条件,退出循环
填入“i≥11”或“i>10”.
故答案为:“i≥11”或“i>10”.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤
17.已知向量,的坐标分别是(﹣1,2),(3,﹣5),求+,﹣,3,2+3的坐标.
【考点】平面向量的坐标运算.
【分析】直接利用向量的坐标运算化简求解即可.
【解答】解:向量,的坐标分别是(﹣1,2),(3,﹣5),
+=(﹣1,2)+(3,﹣5)=(2,﹣3),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
﹣=(﹣1,2)﹣(3,﹣5)=(﹣4,7),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
3=3(﹣1,2)=(﹣3,6),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
2+3=2(﹣1,2)+3(3,﹣5)
=(﹣2,4)+(9,﹣15)
=(7,﹣11).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
18.已知||=4,||=,
=6,求
(1)(﹣) ;
(2)求|+|.
【考点】平面向量数量积的运算.
【分析】(1)由题意可知:||=4,||=,
=6,则(﹣) = +||2=3;
(2)由|+|===.
【解答】解:(1)由题意可知:||=4,||=,
=6,
则(﹣) = ﹣2= +||2=6﹣3=3,
∴(﹣) =3;
(2)由|+|====,
∴|+|=.
19.求经过直线2x+3y+1=0与x﹣3y+4=0的交点,且与直线3x+4y﹣7=0垂直的直线的方程.
【考点】直线的一般式方程与直线的垂直关系.
【分析】联立,解得x=﹣,y=,设与直线3x+4y﹣7=0垂直的直线的方程4x﹣3y+c=0把(﹣,)代入,能求出结果.
【解答】解:联立,解得x=﹣,y=,
设与直线3x+4y﹣7=0垂直的直线的方程4x﹣3y+c=0
把(﹣,)代入,得c=9
∴所求直线为4x﹣3y+9=0
20.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
【考点】频率分布直方图.
【分析】(1)在频率分直方图中,小矩形的面积等于这一组的频率,根据频率的和等于1建立等式解之即可;
(2)60及以上的分数所在的第三、四、五、六组,从而求出抽样学生成绩的合格率,再利用组中值估算抽样学生的平均分即可.
【解答】解:(Ⅰ)因为各组的频率和等于1,故第四组的频率:f4=1﹣(0.025+0.015
2+0.01+0.005)
10=0.3
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为(0.015+0.03+0.025+0.005)
10=0.75所以,抽样学生成绩的合格率是75%
利用组中值估算抽样学生的平均分45 f1+55 f2+65 f3+75 f4+85 f5+95 f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[﹣,],求函数f(x)的值域.
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】(1)利用函数的图象求出A和函数的周期,求出ω,即可求函数f(x)的解析式;
(2)利用正弦函数的单调增区间直接求解函数f(x)的单调增区间;
(3)通过x∈[﹣,],求出相位的范围,利用正弦函数的值域,求函数f(x)的值域.
【解答】解:(1)由题意知:A=2,T=,
∴ω=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
函数f(x)的解析式:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)由
得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
增区间为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(3)∵x∈[﹣,],
∴,
∴.
∴函数的值域为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
22.已知sinθ、cosθ是关于x的方程x2﹣ax+a=0(a∈R)的两个根.
(1)求cos(﹣θ)+sin(+θ)的值;
(2)求tan(π﹣θ)﹣的值.?
【考点】三角函数的化简求值.
【分析】由△≥0可得a的范围,由韦达定理和同角三角函数的基本关系可得a的方程,可得sin
θ+cos
θ=sin
θcos
θ=1﹣.
(1)由诱导公式可得cos()+sin()=sin
θ+cos
θ,
(2)化简可得原式=﹣,代入可得.
【解答】解:由已知原方程判别式△=(﹣a)2﹣4a≥0,
解得a≥4或a≤0.又
∴(sin
θ+cos
θ)2=1+2sin
θcos
θ,即a2﹣2a﹣1=0.
∴a=1﹣或a=1+(舍去).
∴sin
θ+cos
θ=sin
θcos
θ=1﹣.
(1)由诱导公式可得cos()+sin()=sin
θ+cos
θ=1﹣.
(2)tan(π﹣θ)﹣=﹣tan
θ﹣
=﹣(tanθ+)=﹣(+)
=﹣=﹣=+1.
2016年12月28日
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.sin(﹣π)的值是( )
A.
B.
C.﹣
D.﹣
2.已知ABCD为平行四边形,若向量,,则向量为( )
A.﹣
B.
+
C.﹣
D.﹣﹣
3.函数y=sin2x是( )
A.周期为π的奇函数
B.周期为π的偶函数
C.周期为2π的奇函数
D.周期为2π的偶函数
4.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( )
A.
B.
C.
D.
5.已知sinα=,并且α是第二象限的角,那么tanα的值等于( )
A.﹣
B.﹣
C.
D.
6.如图所示,随机在图中撒一把豆子,则它落到阴影部分的概率是( )
A.
B.
C.
D.
7.函数y=cos(2x+)的图象的一条对称轴方程是( )
A.x=﹣
B.x=﹣
C.x=
D.x=π
8.直线4x+3y=40与圆x2+y2=100的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
9.一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是( )
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
10.某班学生在一次数学考试中各分数段以及人数的成绩分布为:[0,80),2人;[80,90),6人;[90,100),4人;[100,110),8人;[110,120),12人;[120,130),5人;[130,140),6人;[140,150),2人.那么分数在[100,130)中的频数以及频率分别为( )
A.25,0.56
B.20,0.56
C.25,0.50
D.13,0.29
11.要得到函数y=cosx的图象,只需将函数y=sin(2x+)的图象上所有的点的( )
A.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度
12.函数f(x)=若f(1)+f(a)=2,则a的所有可能值为( )
A.1
B.﹣
C.1,﹣
D.1,
二、填空题:本大题共4小题,每小题4分,共20分.
13.圆x2﹣4x+y2﹣21=0的半径为 .
14.已知向量,向量=(x,3),且,则x= .
15.某中学高一、高二、高三学生人数之比依次为2:3:5,现用分层抽样的方法抽出一个样本空量为n的样本,样本中高三学生有150人,那么n的值等于 .
16.如图给出的是计算+++…+的值的一个流程图,其中判断框内应填入的条件是
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤
17.已知向量,的坐标分别是(﹣1,2),(3,﹣5),求+,﹣,3,2+3的坐标.
18.已知||=4,||=,
=6,求
(1)(﹣) ;
(2)求|+|.
19.求经过直线2x+3y+1=0与x﹣3y+4=0的交点,且与直线3x+4y﹣7=0垂直的直线的方程.
20.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[﹣,],求函数f(x)的值域.
22.已知sinθ、cosθ是关于x的方程x2﹣ax+a=0(a∈R)的两个根.
(1)求cos(﹣θ)+sin(+θ)的值;
(2)求tan(π﹣θ)﹣的值.?
2016-2017学年山东省济宁市微山一中高二(上)入学数学试卷(文科)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.sin(﹣π)的值是( )
A.
B.
C.﹣
D.﹣
【考点】三角函数的化简求值.
【分析】利用诱导公式以及特殊角的三角函数化简求值即可.
【解答】解:sin(﹣π)=﹣sin=﹣.
故选:D.
2.已知ABCD为平行四边形,若向量,,则向量为( )
A.﹣
B.
+
C.﹣
D.﹣﹣
【考点】平面向量的基本定理及其意义.
【分析】如图所示,利用向量的减法法则即可得出.
【解答】解:如图所示,
由向量的减法法则可得:
==.
故选C.
3.函数y=sin2x是( )
A.周期为π的奇函数
B.周期为π的偶函数
C.周期为2π的奇函数
D.周期为2π的偶函数
【考点】三角函数的周期性及其求法.
【分析】利用正弦函数的奇偶性与周期性即可得到答案.
【解答】解:∵y=f(x)=sin2x,
∴T==π,
又f(﹣x)=sin2(﹣x)=﹣sin2x=﹣f(x),
∴y=sin2x是奇函数,
∴y=sin2x是周期为π的奇函数,
故选:A.
4.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是( )
A.
B.
C.
D.
【考点】等可能事件的概率.
【分析】简化模型,只考虑第999次出现的结果,有两种结果,第999次出现正面朝上只有一种结果,即可求
【解答】解:抛掷一枚质地均匀的硬币,只考虑第999次,有两种结果:正面朝上,反面朝上,每中结果等可能出现,故所求概率为
故选D
5.已知sinα=,并且α是第二象限的角,那么tanα的值等于( )
A.﹣
B.﹣
C.
D.
【考点】同角三角函数基本关系的运用.
【分析】由角的正弦值和角所在的象限,求出角的余弦值,然后,正弦值除以余弦值得正切值.
【解答】解:∵sinα=且α是第二象限的角,
∴,
∴,
故选A
6.如图所示,随机在图中撒一把豆子,则它落到阴影部分的概率是( )
A.
B.
C.
D.
【考点】几何概型.
【分析】由题意知本题是一个几何概型,试验包含的所有事件对应的图形是整个圆.而满足条件的事件对应的是阴影部分,根据几何概型概率公式得到结果.
【解答】解:由题意知本题是一个几何概型,
试验包含的所有事件是对应的图形是整个圆,
而满足条件的事件是事件对应的是阴影部分,
由几何概型概率公式得到P==.
故选C.
7.函数y=cos(2x+)的图象的一条对称轴方程是( )
A.x=﹣
B.x=﹣
C.x=
D.x=π
【考点】余弦函数的对称性.
【分析】根据三角函数的图象,三角函数的函数值取最值时,对称轴的x取值.
【解答】解:此函数的对称轴方程为,当k=0时,.
故选B.
8.直线4x+3y=40与圆x2+y2=100的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
【考点】直线与圆的位置关系.
【分析】由圆的标准方程,求得圆心与半径,根据圆心到直线的距离与半径的大小关系,确定直线与圆的位置关系.
【解答】解:圆x2+y2=100的圆心为原点(0,0),半径r=10.
由圆心(0,0)到直线4x+3y=40的距离d==8,
由d<r,
∴直线4x+3y=40与圆x2+y2=100相交,
故选:A.
9.一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是( )
A.至多有一次中靶
B.两次都中靶
C.只有一次中靶
D.两次都不中靶
【考点】互斥事件与对立事件.
【分析】直接根据对立事件的定义,可得事件“至少有一次中靶”的对立事件,从而得出结论.
【解答】解:根据对立事件的定义可得,事件“至少有一次中靶”的对立事件是:两次都不中靶,
故选D.
10.某班学生在一次数学考试中各分数段以及人数的成绩分布为:[0,80),2人;[80,90),6人;[90,100),4人;[100,110),8人;[110,120),12人;[120,130),5人;[130,140),6人;[140,150),2人.那么分数在[100,130)中的频数以及频率分别为( )
A.25,0.56
B.20,0.56
C.25,0.50
D.13,0.29
【考点】频率分布表;频率分布直方图.
【分析】频数与总数的比为频率,由此能求出结果.
【解答】解:分数在[100,130)的频数为:8+12+5=25,
样本容量为2+6+4+8+12+5+6+2=45,
所求的频率值为:≈0.56.
故选:A.
11.要得到函数y=cosx的图象,只需将函数y=sin(2x+)的图象上所有的点的( )
A.横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度
B.横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】根据题意,有y=sin(2x+)=cos(﹣2x﹣)=,再由变换规律可得答案.
【解答】解:∵y=sin(2x+)==
答案为C
故选C
12.函数f(x)=若f(1)+f(a)=2,则a的所有可能值为( )
A.1
B.﹣
C.1,﹣
D.1,
【考点】分段函数的解析式求法及其图象的作法.
【分析】由分段函数的解析式容易得出,f(1)=e1﹣1=1,∴f(a)=1,然后在每一段上求函数的值为1时对应的a的值即可.
【解答】解:由题意知,当﹣1<x<0时,f(x)=sin(πx2);
当x≥0时,f(x)=ex﹣1;
∴f(1)=e1﹣1=1.
若f(1)+f(a)=2,则f(a)=1;
当a≥0时,ea﹣1=1,∴a=1;
当﹣1<a<0时,sin(πx2)=1,
∴,x=(不满足条件,舍去),或x=.
所以a的所有可能值为:1,.
故答案为:C
二、填空题:本大题共4小题,每小题4分,共20分.
13.圆x2﹣4x+y2﹣21=0的半径为 5 .
【考点】圆的一般方程.
【分析】将一般方程化为标准方程,即可得到圆的半径.
【解答】解:圆x2﹣4x+y2﹣21=0化为标准方程为(x﹣2)2+y2=25
∴圆的半径为5
故答案为:5
14.已知向量,向量=(x,3),且,则x= 6 .
【考点】平面向量共线(平行)的坐标表示.
【分析】根据所给的两个向量的坐标和两个向量平行的充要条件,得到关于x的方程,解方程即可得到要求的x的值.
【解答】解:因为向量,向量=(x,3),且,根据向量共线的充要条件得4×3=2x,x=6
故答案为:6.
15.某中学高一、高二、高三学生人数之比依次为2:3:5,现用分层抽样的方法抽出一个样本空量为n的样本,样本中高三学生有150人,那么n的值等于 300 .
【考点】分层抽样方法.
【分析】令高三学生在所有学生中所占的比例等于抽到的高三学生与样本容量的比,列出方程,求出n的值.
【解答】解:∵高一、高二、高三学生人数之比依次为2:3:5
∴
解得n=300
故答案为:300
16.如图给出的是计算+++…+的值的一个流程图,其中判断框内应填入的条件是 “i≥11”或“i>10”
【考点】程序框图.
【分析】由本程序的功能是计算+++…+的值,由S=S+,故我们知道最后一次进行循环时的条件为i=10,当i≥11应退出循环输出S的值,由此不难得到判断框中的条件.
【解答】解:∵S=+++…+
并由流程图中S=S+
故循环的初值为1
终值为10、步长为1
故经过10次循环才能算出S=+++…+的值,
故i≤10,应不满足条件,继续循环
∴当i≥11,应满足条件,退出循环
填入“i≥11”或“i>10”.
故答案为:“i≥11”或“i>10”.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤
17.已知向量,的坐标分别是(﹣1,2),(3,﹣5),求+,﹣,3,2+3的坐标.
【考点】平面向量的坐标运算.
【分析】直接利用向量的坐标运算化简求解即可.
【解答】解:向量,的坐标分别是(﹣1,2),(3,﹣5),
+=(﹣1,2)+(3,﹣5)=(2,﹣3),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
﹣=(﹣1,2)﹣(3,﹣5)=(﹣4,7),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
3=3(﹣1,2)=(﹣3,6),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
2+3=2(﹣1,2)+3(3,﹣5)
=(﹣2,4)+(9,﹣15)
=(7,﹣11).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
18.已知||=4,||=,
=6,求
(1)(﹣) ;
(2)求|+|.
【考点】平面向量数量积的运算.
【分析】(1)由题意可知:||=4,||=,
=6,则(﹣) = +||2=3;
(2)由|+|===.
【解答】解:(1)由题意可知:||=4,||=,
=6,
则(﹣) = ﹣2= +||2=6﹣3=3,
∴(﹣) =3;
(2)由|+|====,
∴|+|=.
19.求经过直线2x+3y+1=0与x﹣3y+4=0的交点,且与直线3x+4y﹣7=0垂直的直线的方程.
【考点】直线的一般式方程与直线的垂直关系.
【分析】联立,解得x=﹣,y=,设与直线3x+4y﹣7=0垂直的直线的方程4x﹣3y+c=0把(﹣,)代入,能求出结果.
【解答】解:联立,解得x=﹣,y=,
设与直线3x+4y﹣7=0垂直的直线的方程4x﹣3y+c=0
把(﹣,)代入,得c=9
∴所求直线为4x﹣3y+9=0
20.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
【考点】频率分布直方图.
【分析】(1)在频率分直方图中,小矩形的面积等于这一组的频率,根据频率的和等于1建立等式解之即可;
(2)60及以上的分数所在的第三、四、五、六组,从而求出抽样学生成绩的合格率,再利用组中值估算抽样学生的平均分即可.
【解答】解:(Ⅰ)因为各组的频率和等于1,故第四组的频率:f4=1﹣(0.025+0.015
2+0.01+0.005)
10=0.3
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为(0.015+0.03+0.025+0.005)
10=0.75所以,抽样学生成绩的合格率是75%
利用组中值估算抽样学生的平均分45 f1+55 f2+65 f3+75 f4+85 f5+95 f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71.
21.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[﹣,],求函数f(x)的值域.
【考点】函数y=Asin(ωx+φ)的图象变换.
【分析】(1)利用函数的图象求出A和函数的周期,求出ω,即可求函数f(x)的解析式;
(2)利用正弦函数的单调增区间直接求解函数f(x)的单调增区间;
(3)通过x∈[﹣,],求出相位的范围,利用正弦函数的值域,求函数f(x)的值域.
【解答】解:(1)由题意知:A=2,T=,
∴ω=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
函数f(x)的解析式:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)由
得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
增区间为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(3)∵x∈[﹣,],
∴,
∴.
∴函数的值域为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
22.已知sinθ、cosθ是关于x的方程x2﹣ax+a=0(a∈R)的两个根.
(1)求cos(﹣θ)+sin(+θ)的值;
(2)求tan(π﹣θ)﹣的值.?
【考点】三角函数的化简求值.
【分析】由△≥0可得a的范围,由韦达定理和同角三角函数的基本关系可得a的方程,可得sin
θ+cos
θ=sin
θcos
θ=1﹣.
(1)由诱导公式可得cos()+sin()=sin
θ+cos
θ,
(2)化简可得原式=﹣,代入可得.
【解答】解:由已知原方程判别式△=(﹣a)2﹣4a≥0,
解得a≥4或a≤0.又
∴(sin
θ+cos
θ)2=1+2sin
θcos
θ,即a2﹣2a﹣1=0.
∴a=1﹣或a=1+(舍去).
∴sin
θ+cos
θ=sin
θcos
θ=1﹣.
(1)由诱导公式可得cos()+sin()=sin
θ+cos
θ=1﹣.
(2)tan(π﹣θ)﹣=﹣tan
θ﹣
=﹣(tanθ+)=﹣(+)
=﹣=﹣=+1.
2016年12月28日
同课章节目录
