四川省成都经济技术开发区实验中学校2017届高三上学期期末模拟考试数学(理)试题
文档属性
| 名称 | 四川省成都经济技术开发区实验中学校2017届高三上学期期末模拟考试数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 359.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-30 00:00:00 | ||
图片预览


文档简介
成都经开区实验中学2014级高三上期期末考试模拟试卷
数
学(理工类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
注意事项:
1.必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.
2.考试结束后,将本试题卷和答题卡一并交回。
选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则集合等于
A.
B.
C.
D.
2.已知i为虚数单位,(1﹣2i) z=i3.则复数z在复平面内对应的点在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.一个几何体的三视图及其尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为
( http: / / www.21cnjy.com )
A.
B.
C.
D.
4.设,函数,则使的的取值范围是
A.
B.
C.
D.
5.
已知函数,则的最大值为
A.
B.
C.
D.
6、已知点在经过两点的直线上,则的最小值为
A.
B.
C.
D.不存在
7.
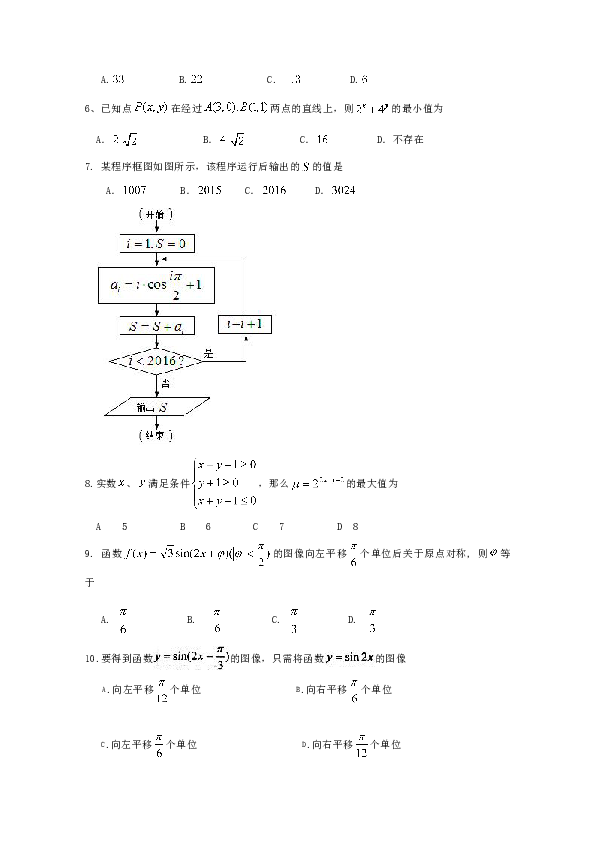
某程序框图如图所示,该程序运行后输出的的值是
A.
B.
C.
D.
( http: / / www.21cnjy.com )
8.实数、满足条件,那么的最大值为
A 5
B 6
C 7
D 8
9.
函数的图像向左平移个单位后关于原点对称,
则等于
A.
B.
C.
D.
10.要得到函数的图像,只需将函数的图像
A.向左平移个单位
B.向右平移个单位
C.向左平移个单位
D.向右平移个单位
11.已知甲盒中仅有1个球且为红球,乙盒中有个红球和个篮球,从乙盒中随机抽取个球放入甲盒中.
(a)放入个球后,甲盒中含有红球的个数记为;
(b)放入个球后,从甲盒中取1个球是红球的概率记为.则
A.
B.
C.
D.
12.
已知函数满足:,那么下列不等式成立的是
A.
B.
C.
D.
第Ⅱ卷(非选择题,共90分)
二、填空题(每小题4分,共20分)
13.二项式(﹣)6展开式中常数项为
.
14.已知,则=
.
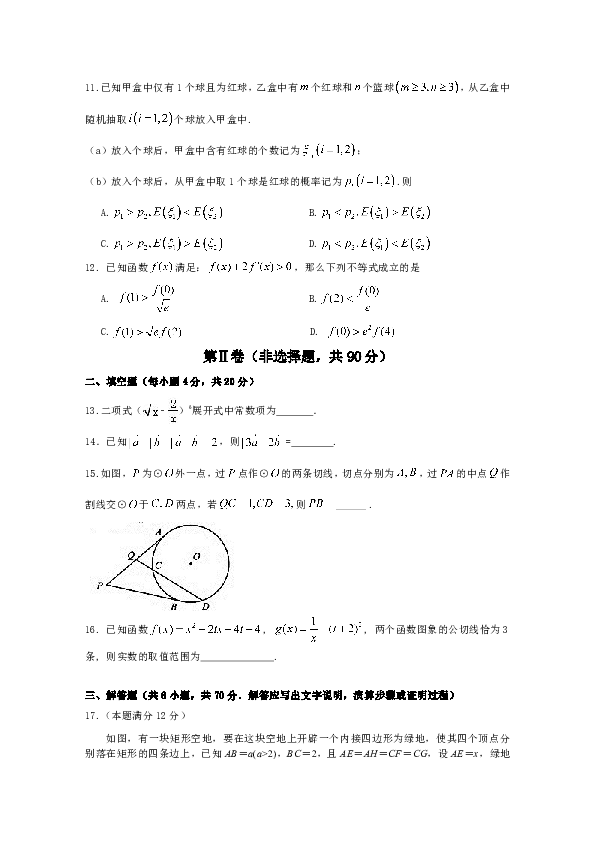
15.如图,为⊙外一点,过点作⊙的两条切线,切点分别为,过的中点作割线交⊙于两点,若则.
( http: / / www.21cnjy.com )
16.
已知函数,
,
两个函数图象的公切线恰为3条,
则实数的取值范围为
.
三、解答题(共6小题,共70分.解答应写出文字说明,演算步骤或证明过程)
17.(本题满分12分)
如图,有一块矩形空地,要在这块空
( http: / / www.21cnjy.com )地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,并指出这个函数的定义域.
(2)当AE为何值时,绿地面积y最大?
18.(本题满分12分)
已知向量,,函数.
(1)求函数的解析式;
(2)当时,求的单调递增区间;
19.(本小题满分12分)
已知函数的最大值为2.
(Ⅰ)求函数在上的单调递减区间;
(Ⅱ)△ABC中,,角A、B、C所对的边分别是a、b、c,且,c=3,求△ABC的面积..
20.(本小题满分12分)
已知函数,,
(1)当时,函数f(x)为递减函数,求的取值范围;
(2)设是函数的导函数,是函数的两个零点,且,求证
(3)证明当时,
患有颈椎疾病
没有患颈椎疾病
合计
白领
5
蓝领
10
合计
50
21.为了了解某工业园中员工的颈椎疾病与工
( http: / / www.21cnjy.com )作性质是否有关,在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查,得到如右的列联表.
已知在全部50人中随机抽取1人,抽到患有颈椎疾病的人的概率为.
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为患颈椎疾病与工作性质有关?说明你的理由;
(2)已知在患有颈椎疾病的10名蓝领中,有3为工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为,求的分布列及数学期望.
参考公式:,其中.
下面的临界值表仅供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分。作答时请写清题号,本小题满分10分。
22.选修4
-
4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点,极轴与轴的正半轴重合,曲线的极坐标方程为,直线的参数方程为(为参数,),
(1)求曲线与直线在直角坐标系中的普通方程;
(2)试在曲线上求一点,使它到直线的距离最大,并求出点的极坐标.
23.(本题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-
2|-|2x+l|.
(I)求不等式f(x)≤x的解集;
(II
)若不等式f(x)≥t2一t在x∈[-2,-1]时恒成立,求实数t的取值范围.
成都经开区实验中学2014级高三上期期末考试模拟试卷
数学(理工类)参考答案
1—5
CDBCC
6—10
BDDDB
11—12
AA
13.60
14.
15.
4
16.
17.解 (1)S△AEH=S△CFG=x2,
S△BEF=S△DGH=(a-x)(2-x).
∴y=S矩形ABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)
=-2x2+(a+2)
x.
4分
由,得0∴y=-2x2+(a+2)x,定义域为(0,2].
6分
(2)当<2,即a<6时,则x=时,y取最大值;
8分
当≥2,即a≥6时,y=-2x2+(a+2)x,
在(0,2]上是增函数,则x=2时,ymax=2a-4.
11分
综上所述:当a<6,AE=时,绿地面积取最大值;
当a≥6,AE=2时,绿地面积取最大值2a-4.
12分
18.【解】(1)∵
∴
∴
(2)由,
解得,
∵取和且,得和,
∴的单调递增区间为和
法二:∵,∴,
∴由和,
解得和,
∴的单调递增区间为和
19.【解析】(1)由题意,的最大值为,所以.
而,于是,.
为递减函数,则满足
,
即.
所以在上的单调递减区间为.
……………….5分
(2)设△ABC的外接圆半径为,由题意,得.
化简,得
.
由正弦定理,
得,.
①…………………….8分
由余弦定理,得,即.
②……………….10分
将①式代入②,得.
解得,或
(舍去)..
……………….12分
20.试题解析:(1)
(2)由于是函数的两个零点,且
所以,
两式相减得:,
( http: / / www.21cnjy.com )
要证明,只需证,即只需证
( http: / / www.21cnjy.com )
设,构造函数
在单调递增,
( http: / / www.21cnjy.com ),
(3)由(1)可知,a=1时,x>1,
,
21.【答案】(1)我们有99.5%的把握认为患颈椎疾病是与工作性质有关系的;(2)
【解析】解:(Ⅰ)根据在全部50人中随机抽取1人患颈椎疾病的概率为,
患有颈椎疾病
没有患颈椎疾病
合计
白领
20
5
25
蓝领
10
15
25
合计
30
20
50
可得患颈椎疾病的为30人,故可得列联表如右:
因为,
即,
所以,
又,
所以,我们有99.5%的把握认为患颈椎疾病是与工作性质有关系的.
(Ⅱ)现在从患颈椎疾病的10名蓝领中,选出3名进行工龄的调查,
记选出工龄在15年以上的人数为,则.
故,,,,
则的分布列为:
0
1
2
3
P
则.
22.解:
(Ⅰ)曲线C的普通方程是,直线的普通方程是。
(Ⅱ)设点M的直角坐标是,则点M到直线的距离是
因为,所以当,即即时,取得最大值。此时
综上,点M的极坐标为时,该点到直线的距离最大。
23.解析:
.
( http: / / www.21cnjy.com )
数
学(理工类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
注意事项:
1.必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.
2.考试结束后,将本试题卷和答题卡一并交回。
选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,则集合等于
A.
B.
C.
D.
2.已知i为虚数单位,(1﹣2i) z=i3.则复数z在复平面内对应的点在
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.一个几何体的三视图及其尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,则这个几何体的表面积为
( http: / / www.21cnjy.com )
A.
B.
C.
D.
4.设,函数,则使的的取值范围是
A.
B.
C.
D.
5.
已知函数,则的最大值为
A.
B.
C.
D.
6、已知点在经过两点的直线上,则的最小值为
A.
B.
C.
D.不存在
7.
某程序框图如图所示,该程序运行后输出的的值是
A.
B.
C.
D.
( http: / / www.21cnjy.com )
8.实数、满足条件,那么的最大值为
A 5
B 6
C 7
D 8
9.
函数的图像向左平移个单位后关于原点对称,
则等于
A.
B.
C.
D.
10.要得到函数的图像,只需将函数的图像
A.向左平移个单位
B.向右平移个单位
C.向左平移个单位
D.向右平移个单位
11.已知甲盒中仅有1个球且为红球,乙盒中有个红球和个篮球,从乙盒中随机抽取个球放入甲盒中.
(a)放入个球后,甲盒中含有红球的个数记为;
(b)放入个球后,从甲盒中取1个球是红球的概率记为.则
A.
B.
C.
D.
12.
已知函数满足:,那么下列不等式成立的是
A.
B.
C.
D.
第Ⅱ卷(非选择题,共90分)
二、填空题(每小题4分,共20分)
13.二项式(﹣)6展开式中常数项为
.
14.已知,则=
.
15.如图,为⊙外一点,过点作⊙的两条切线,切点分别为,过的中点作割线交⊙于两点,若则.
( http: / / www.21cnjy.com )
16.
已知函数,
,
两个函数图象的公切线恰为3条,
则实数的取值范围为
.
三、解答题(共6小题,共70分.解答应写出文字说明,演算步骤或证明过程)
17.(本题满分12分)
如图,有一块矩形空地,要在这块空
( http: / / www.21cnjy.com )地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,并指出这个函数的定义域.
(2)当AE为何值时,绿地面积y最大?
18.(本题满分12分)
已知向量,,函数.
(1)求函数的解析式;
(2)当时,求的单调递增区间;
19.(本小题满分12分)
已知函数的最大值为2.
(Ⅰ)求函数在上的单调递减区间;
(Ⅱ)△ABC中,,角A、B、C所对的边分别是a、b、c,且,c=3,求△ABC的面积..
20.(本小题满分12分)
已知函数,,
(1)当时,函数f(x)为递减函数,求的取值范围;
(2)设是函数的导函数,是函数的两个零点,且,求证
(3)证明当时,
患有颈椎疾病
没有患颈椎疾病
合计
白领
5
蓝领
10
合计
50
21.为了了解某工业园中员工的颈椎疾病与工
( http: / / www.21cnjy.com )作性质是否有关,在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查,得到如右的列联表.
已知在全部50人中随机抽取1人,抽到患有颈椎疾病的人的概率为.
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为患颈椎疾病与工作性质有关?说明你的理由;
(2)已知在患有颈椎疾病的10名蓝领中,有3为工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为,求的分布列及数学期望.
参考公式:,其中.
下面的临界值表仅供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分。作答时请写清题号,本小题满分10分。
22.选修4
-
4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点,极轴与轴的正半轴重合,曲线的极坐标方程为,直线的参数方程为(为参数,),
(1)求曲线与直线在直角坐标系中的普通方程;
(2)试在曲线上求一点,使它到直线的距离最大,并求出点的极坐标.
23.(本题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-
2|-|2x+l|.
(I)求不等式f(x)≤x的解集;
(II
)若不等式f(x)≥t2一t在x∈[-2,-1]时恒成立,求实数t的取值范围.
成都经开区实验中学2014级高三上期期末考试模拟试卷
数学(理工类)参考答案
1—5
CDBCC
6—10
BDDDB
11—12
AA
13.60
14.
15.
4
16.
17.解 (1)S△AEH=S△CFG=x2,
S△BEF=S△DGH=(a-x)(2-x).
∴y=S矩形ABCD-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)
=-2x2+(a+2)
x.
4分
由,得0
6分
(2)当<2,即a<6时,则x=时,y取最大值;
8分
当≥2,即a≥6时,y=-2x2+(a+2)x,
在(0,2]上是增函数,则x=2时,ymax=2a-4.
11分
综上所述:当a<6,AE=时,绿地面积取最大值;
当a≥6,AE=2时,绿地面积取最大值2a-4.
12分
18.【解】(1)∵
∴
∴
(2)由,
解得,
∵取和且,得和,
∴的单调递增区间为和
法二:∵,∴,
∴由和,
解得和,
∴的单调递增区间为和
19.【解析】(1)由题意,的最大值为,所以.
而,于是,.
为递减函数,则满足
,
即.
所以在上的单调递减区间为.
……………….5分
(2)设△ABC的外接圆半径为,由题意,得.
化简,得
.
由正弦定理,
得,.
①…………………….8分
由余弦定理,得,即.
②……………….10分
将①式代入②,得.
解得,或
(舍去)..
……………….12分
20.试题解析:(1)
(2)由于是函数的两个零点,且
所以,
两式相减得:,
( http: / / www.21cnjy.com )
要证明,只需证,即只需证
( http: / / www.21cnjy.com )
设,构造函数
在单调递增,
( http: / / www.21cnjy.com ),
(3)由(1)可知,a=1时,x>1,
,
21.【答案】(1)我们有99.5%的把握认为患颈椎疾病是与工作性质有关系的;(2)
【解析】解:(Ⅰ)根据在全部50人中随机抽取1人患颈椎疾病的概率为,
患有颈椎疾病
没有患颈椎疾病
合计
白领
20
5
25
蓝领
10
15
25
合计
30
20
50
可得患颈椎疾病的为30人,故可得列联表如右:
因为,
即,
所以,
又,
所以,我们有99.5%的把握认为患颈椎疾病是与工作性质有关系的.
(Ⅱ)现在从患颈椎疾病的10名蓝领中,选出3名进行工龄的调查,
记选出工龄在15年以上的人数为,则.
故,,,,
则的分布列为:
0
1
2
3
P
则.
22.解:
(Ⅰ)曲线C的普通方程是,直线的普通方程是。
(Ⅱ)设点M的直角坐标是,则点M到直线的距离是
因为,所以当,即即时,取得最大值。此时
综上,点M的极坐标为时,该点到直线的距离最大。
23.解析:
.
( http: / / www.21cnjy.com )
同课章节目录
