2.5一元二次方程的应用图形面积问题专题检测题(含答案)
文档属性
| 名称 | 2.5一元二次方程的应用图形面积问题专题检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-30 00:00:00 | ||
图片预览

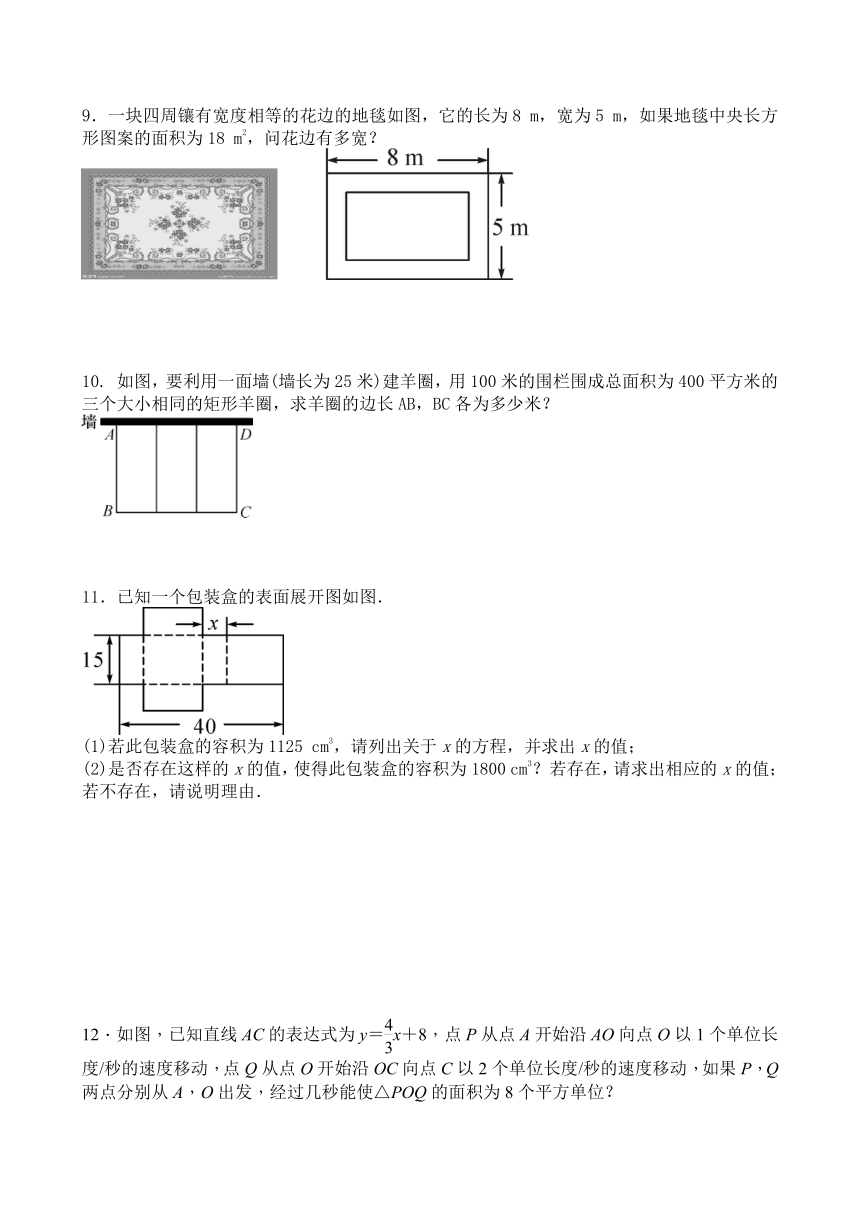
文档简介
湘教版数学九年级上册
第2章
一元二次方程
2.5 一元二次方程的应用
图形面积问题
专题检测题
1.一根长为22
m的铁丝,恰好折成一个面积为30
m2的矩形,则这个矩形的长是(
)
A.5
m
B.6
m
C.7
m
D.10
m
2.一边靠6
m长的墙,其他三边用长为13
m的篱笆围成的长方形鸭舍的面积为20
m2,那么这个长方形鸭舍与墙垂直的一边的长是(
)
A.4
m
B.2.5
m
C.2
m
D.4
m或2.5
m
3.(易错题)某杂技团用68
m长的幕布围成一个面积为300
m2的矩形临时场地,并留出2
m作为出入口,则矩形场地的长为(
)
A.15
m
B.20
m
C.25
m
D.30
m
4.如图,在△ABC中,∠ABC=90°,AB=8
cm,BC=6
cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1
cm/秒,点Q的速度为2
cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间中,能使△PBQ的面积为15
cm2的是(
)
A.2秒钟
B.3秒钟
C.4秒钟
D.5秒钟
5.如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米,若设道路宽为x米,则根据题意可列出方程为_______________________.
6.如图是一张长9
cm、宽5
cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12
cm2的一个无盖长方体纸盒,设剪去的正方形边长为x
cm.则可列出关于x的方程为_______________________________.
7.
如图,某小区规划在一个长30
m、宽20
m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,要使每一块花草的面积都为78
m2,那么通道的宽应设计成多少m?设通道的宽为x
m,由题意列方程为____________________________.
8.要用一根长为24
cm的铁丝围成一个斜边为10
m的直角三角形,则两直角边的长分别为____________________.
9.一块四周镶有宽度相等的花边的地毯如图,它的长为8
m,宽为5
m,如果地毯中央长方形图案的面积为18
m2,问花边有多宽?
10.
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
11.已知一个包装盒的表面展开图如图.
(1)若此包装盒的容积为1125
cm3,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得此包装盒的容积为1800
cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
12.如图,已知直线AC的表达式为y=x+8,点P从点A开始沿AO向点O以1个单位长度/秒的速度移动,点Q从点O开始沿OC向点C以2个单位长度/秒的速度移动,如果P,Q两点分别从A,O出发,经过几秒能使△POQ的面积为8个平方单位?
13.如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5
m,墙外可用宽度为3.25
m.现有长为21
m的篱笆,计划靠着院墙围成一个中间有一道隔栏的矩形花圃.
(1)若要围成总面积为36
m2的花圃,边AB的长应是多少?
(2)花圃的面积能否达到36.75
m2?若能,求出边AB的长;若不能,请说明理由.
答案:
1---4
BABB
5.
(17-x)(22-x)=300
6.
(9-2x)(5-2x)=12
7.
(30-2x)(20-x)=78×6
8.
6cm和8cm
9.
解:设花边宽为x
m,则有(8-2x)(5-2x)=18,解得x1=1,x2=5.5.当x=5.5时,8-2x=-3(舍去),∴x=1,即花边宽1
m
10.
解:设AB长x米,则BC长为(100-4x)米,则有x(100-4x)=400,解得x1=20,x2=5,当x=20时,100-4x=20<25.当x=5时,100-4x=80>25(舍去),∴AB长20米,BC长20米
11.
解:(1)根据题意,得15x(20-x)=1125,整理,得x2-20x+75=0.解得x=15(舍去)或x=5.答:包装盒的高为5
cm
(2)根据题意,得15x(20-x)=1800,即x2-20x+120=0.∵Δ=(-20)2-4×1×120=-80<0,∴此方程无解,即不存在这样的x的值,使得包装盒的体积为1800
cm3
12.
解:根据题意,有A(-6,0),C(0,8),OA=6,OC=8,设经过x秒后,△POQ面积为8个平方单位,则有(6-x)·2x÷2=8,解得x1=2,x2=4,当x=2时,OP=6-x=4,OQ=4,符合题意,当x=4时,OP=6-x=2,OQ=8,符合题意.∴经过2秒或4秒后,△POQ的面积为8个平方单位
13.
解:(1)
设AB的长为x米,则长为(21-3x)米,根据题意,得x(21-3x)=36.解得x=3或x=4.∵墙外可用宽度为3.25
m,∴x只能取3.答:边AB的长为3
m
(2)不能.理由:花圃的面积为(21-3x)x=-3(x-3.5)2+36.75,∴当AB长为3.5
m时,有最大面积,为36.75平方米,但由于墙外可用宽度为3.25
m<3.5
m.即花圃的面积不能达到36.75
m2
第2章
一元二次方程
2.5 一元二次方程的应用
图形面积问题
专题检测题
1.一根长为22
m的铁丝,恰好折成一个面积为30
m2的矩形,则这个矩形的长是(
)
A.5
m
B.6
m
C.7
m
D.10
m
2.一边靠6
m长的墙,其他三边用长为13
m的篱笆围成的长方形鸭舍的面积为20
m2,那么这个长方形鸭舍与墙垂直的一边的长是(
)
A.4
m
B.2.5
m
C.2
m
D.4
m或2.5
m
3.(易错题)某杂技团用68
m长的幕布围成一个面积为300
m2的矩形临时场地,并留出2
m作为出入口,则矩形场地的长为(
)
A.15
m
B.20
m
C.25
m
D.30
m
4.如图,在△ABC中,∠ABC=90°,AB=8
cm,BC=6
cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1
cm/秒,点Q的速度为2
cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间中,能使△PBQ的面积为15
cm2的是(
)
A.2秒钟
B.3秒钟
C.4秒钟
D.5秒钟
5.如图,在一块长为22米、宽为17米的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300平方米,若设道路宽为x米,则根据题意可列出方程为_______________________.
6.如图是一张长9
cm、宽5
cm的矩形纸板,将纸板四个角各剪去一个同样的正方形,可制成底面积是12
cm2的一个无盖长方体纸盒,设剪去的正方形边长为x
cm.则可列出关于x的方程为_______________________________.
7.
如图,某小区规划在一个长30
m、宽20
m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,要使每一块花草的面积都为78
m2,那么通道的宽应设计成多少m?设通道的宽为x
m,由题意列方程为____________________________.
8.要用一根长为24
cm的铁丝围成一个斜边为10
m的直角三角形,则两直角边的长分别为____________________.
9.一块四周镶有宽度相等的花边的地毯如图,它的长为8
m,宽为5
m,如果地毯中央长方形图案的面积为18
m2,问花边有多宽?
10.
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
11.已知一个包装盒的表面展开图如图.
(1)若此包装盒的容积为1125
cm3,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得此包装盒的容积为1800
cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
12.如图,已知直线AC的表达式为y=x+8,点P从点A开始沿AO向点O以1个单位长度/秒的速度移动,点Q从点O开始沿OC向点C以2个单位长度/秒的速度移动,如果P,Q两点分别从A,O出发,经过几秒能使△POQ的面积为8个平方单位?
13.如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5
m,墙外可用宽度为3.25
m.现有长为21
m的篱笆,计划靠着院墙围成一个中间有一道隔栏的矩形花圃.
(1)若要围成总面积为36
m2的花圃,边AB的长应是多少?
(2)花圃的面积能否达到36.75
m2?若能,求出边AB的长;若不能,请说明理由.
答案:
1---4
BABB
5.
(17-x)(22-x)=300
6.
(9-2x)(5-2x)=12
7.
(30-2x)(20-x)=78×6
8.
6cm和8cm
9.
解:设花边宽为x
m,则有(8-2x)(5-2x)=18,解得x1=1,x2=5.5.当x=5.5时,8-2x=-3(舍去),∴x=1,即花边宽1
m
10.
解:设AB长x米,则BC长为(100-4x)米,则有x(100-4x)=400,解得x1=20,x2=5,当x=20时,100-4x=20<25.当x=5时,100-4x=80>25(舍去),∴AB长20米,BC长20米
11.
解:(1)根据题意,得15x(20-x)=1125,整理,得x2-20x+75=0.解得x=15(舍去)或x=5.答:包装盒的高为5
cm
(2)根据题意,得15x(20-x)=1800,即x2-20x+120=0.∵Δ=(-20)2-4×1×120=-80<0,∴此方程无解,即不存在这样的x的值,使得包装盒的体积为1800
cm3
12.
解:根据题意,有A(-6,0),C(0,8),OA=6,OC=8,设经过x秒后,△POQ面积为8个平方单位,则有(6-x)·2x÷2=8,解得x1=2,x2=4,当x=2时,OP=6-x=4,OQ=4,符合题意,当x=4时,OP=6-x=2,OQ=8,符合题意.∴经过2秒或4秒后,△POQ的面积为8个平方单位
13.
解:(1)
设AB的长为x米,则长为(21-3x)米,根据题意,得x(21-3x)=36.解得x=3或x=4.∵墙外可用宽度为3.25
m,∴x只能取3.答:边AB的长为3
m
(2)不能.理由:花圃的面积为(21-3x)x=-3(x-3.5)2+36.75,∴当AB长为3.5
m时,有最大面积,为36.75平方米,但由于墙外可用宽度为3.25
m<3.5
m.即花圃的面积不能达到36.75
m2
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
