2017河北中考数学5.2锐角三角函数及解直角三角形的应用教材知识梳理
文档属性
| 名称 | 2017河北中考数学5.2锐角三角函数及解直角三角形的应用教材知识梳理 |
|
|
| 格式 | zip | ||
| 文件大小 | 870.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-01 00:00:00 | ||
图片预览


文档简介
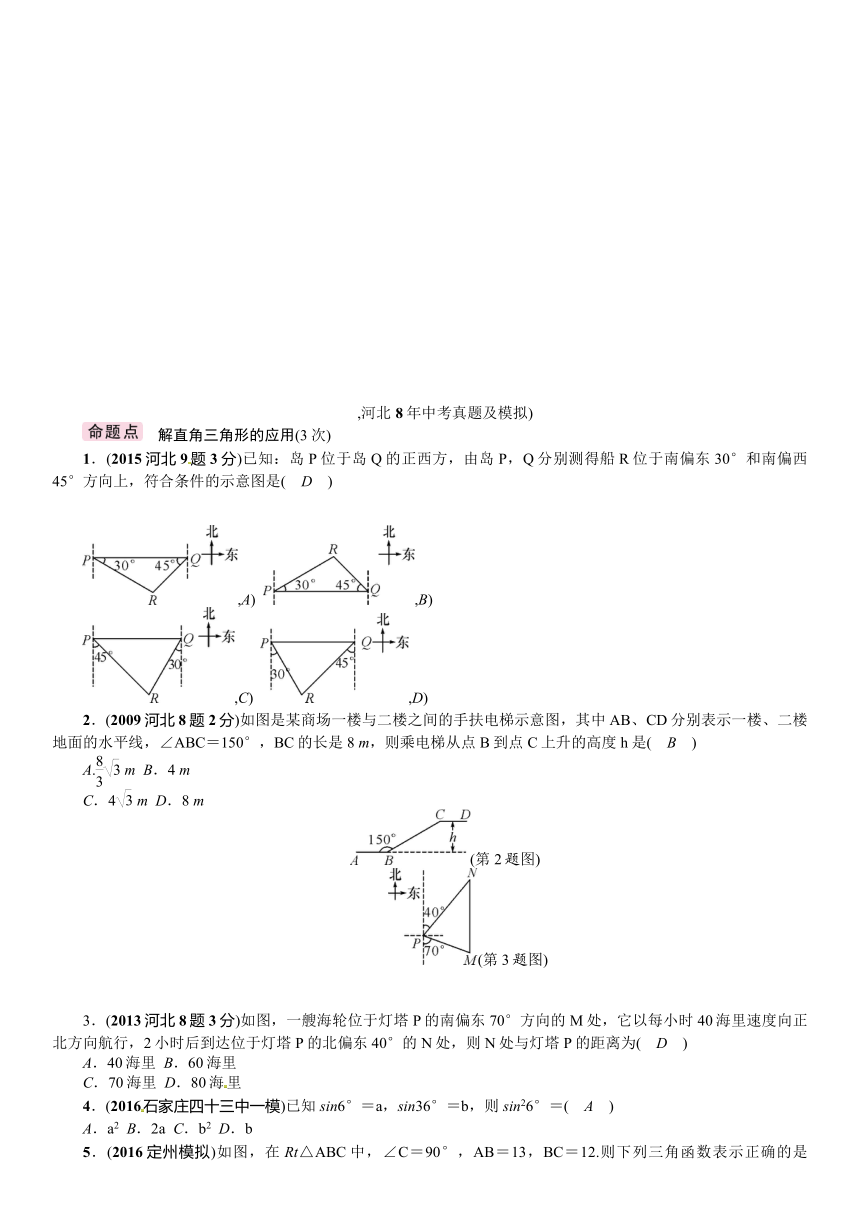
第二节 锐角三角函数及解直角三角形的应用
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2015
9
认识方位角
考查方式依题意画出方位角
3
3
2014
22(3)
解直角三角形的应用
以三个垃圾存放点为背景,(3)通过解直角三角形求垃圾运送费用
4
4
2013
8
解直角三角形的应用
以航行、方向角为背景,利用解直角三角形求距离
3
3
2009
8
解直角三角形的应用
以手扶电梯为背景,利用解直角三角形求高度
2
2
2010、2011、2012、2016四年未考查
命题规律
纵观河北8年中考,锐角三角函数及解直角三角形,在中考中只出一题,题型多为选择和解答题,分值2~9分,难度中等,主要考查解直角三角形的应用的选择题和解答题形式各考查了2次,2015年考查了对方位角的认识,其中2010~2012年都未考查,2016年也没独立考查.
命题预测
预计2017年河北中考,仍然会考此知识点,命选择题可能性较大,也有可能出解答题,应强化训练不留死角
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
解直角三角形的应用(3次)
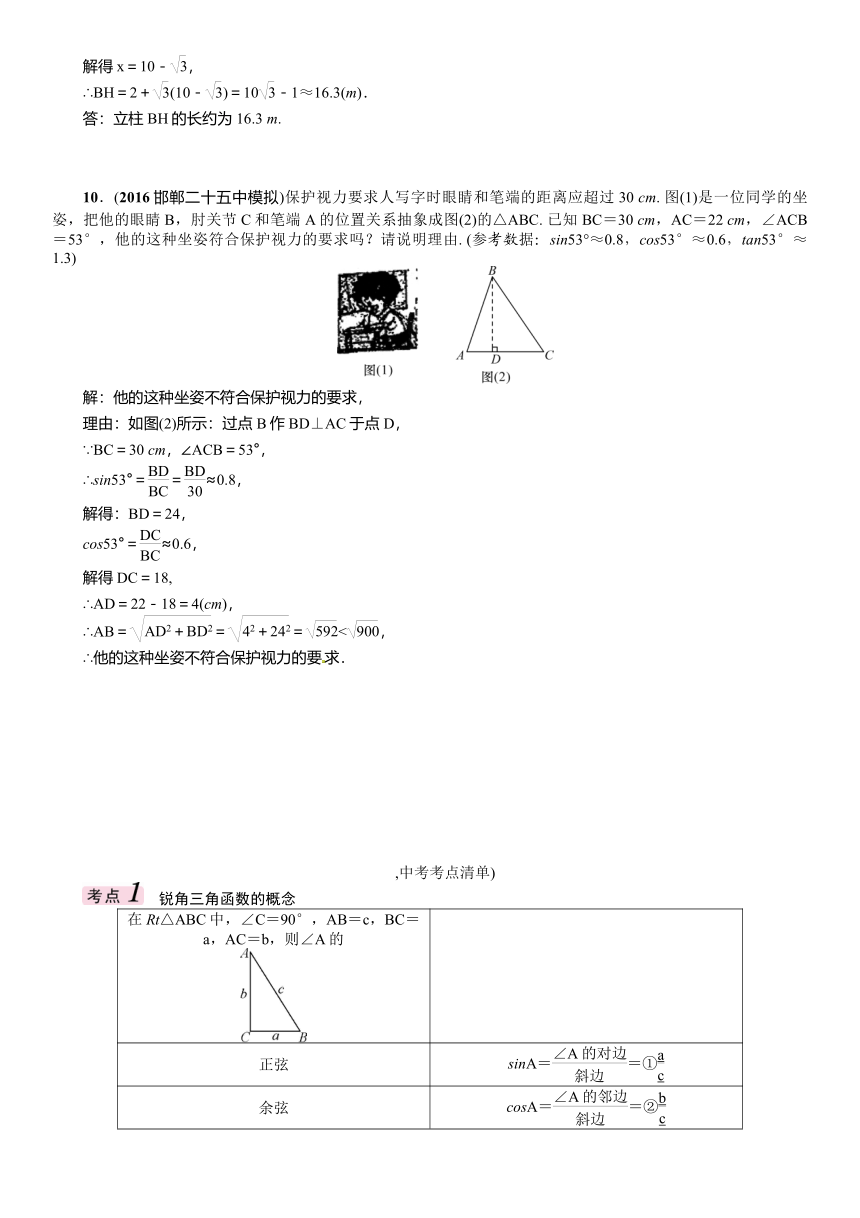
1.(2015河北9题3分)已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( D )
,A)
,B)
,C)
,D)
2.(2009河北8题2分)如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8
m,则乘电梯从点B到点C上升的高度h是( B )
A.
m
B.4
m
C.4
m
D.8
m
(第2题图)
(第3题图)
3.(2013河北8题3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( D )
A.40海里
B.60海里
C.70海里
D.80海里
4.(2016石家庄四十三中一模)已知sin6°=a,sin36°=b,则sin26°=( A )
A.a2
B.2a
C.b2
D.b
5.(2016定州模拟)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12.则下列三角函数表示正确的是( A )
A.sinA=
B.cosA=
C.tanA=
D.tanB=
(第5题图)
(第6题图)
6.(2016唐山二模)如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( B )
A.
B.
C.
D.
(第7题图)
(第8题图)
7.(2016张家口一模)河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( A )
A.5
m
B.10
m
C.15
m
D.10
m
8.(2016保定十三中二模)如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为__2__.
9.(2016张家口九中二模)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引伸出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2
m,两拉索底端距离AD为20
m,请求出立柱BH的长.(结果精确到0.1
m,≈1.732)
解:设DH=x
m,
∵∠CDH=60°,∠H=90°,
∴CH=DH·sin60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,
解得x=10-,
∴BH=2+(10-)=10-1≈16.3(m).
答:立柱BH的长约为16.3
m.
10.(2016邯郸二十五中模拟)保护视力要求人写字时眼睛和笔端的距离应超过30
cm.
图(1)是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图(2)的△ABC.
已知BC=30
cm,AC=22
cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
解:他的这种坐姿不符合保护视力的要求,
理由:如图(2)所示:过点B作BD⊥AC于点D,
∵BC=30
cm,∠ACB=53°,
∴sin53°==≈0.8,
解得:BD=24,
cos53°=≈0.6,
解得DC=18,
∴AD=22-18=4(cm),
∴AB===<,
∴他的这种坐姿不符合保护视力的要求.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
锐角三角函数的概念
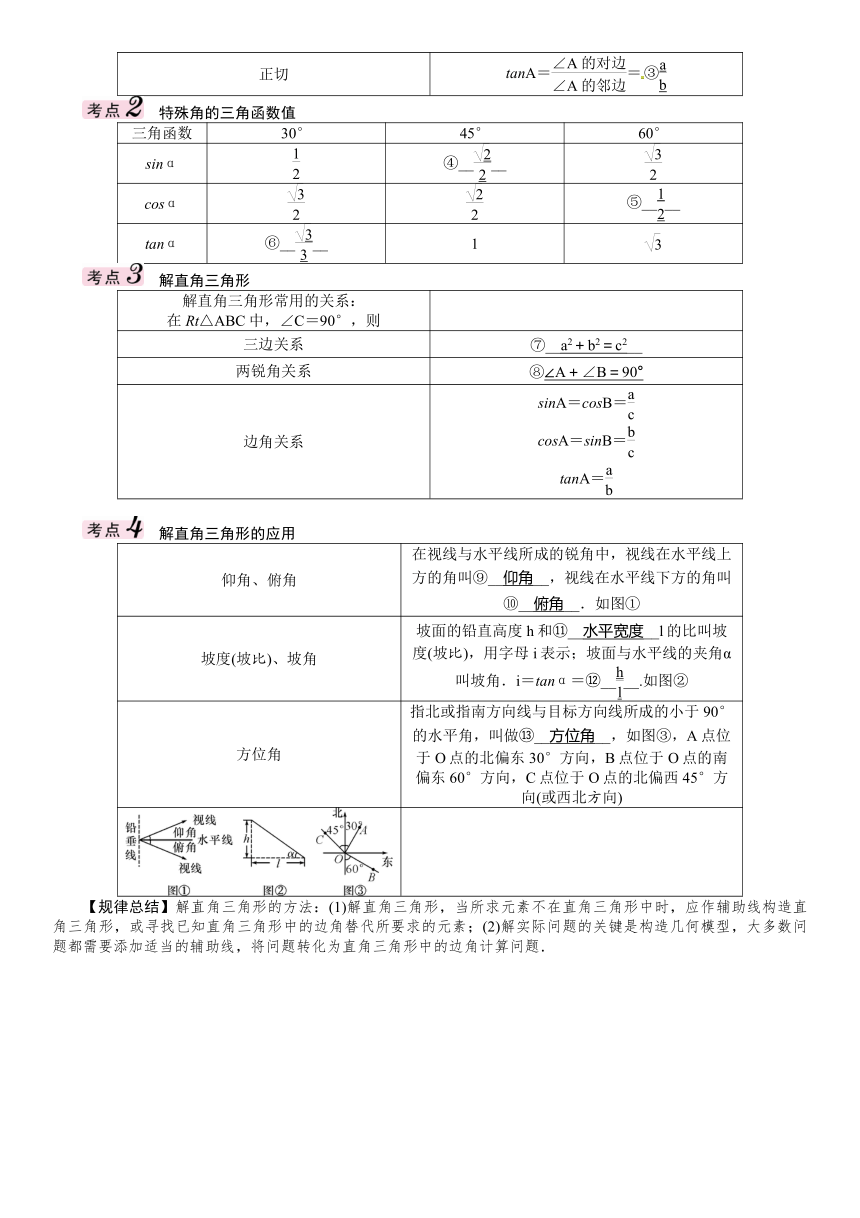
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则∠A的
正弦
sinA==①
余弦
cosA==②
正切
tanA==③
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
特殊角的三角函数值
三角函数
30°
45°
60°
sinα
④____
cosα
⑤____
tanα
⑥____
1
INCLUDEPICTURE"考点3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点3.TIF"
\
MERGEFORMAT
解直角三角形
解直角三角形常用的关系:在Rt△ABC中,∠C=90°,则
三边关系
⑦__a2+b2=c2__
两锐角关系
⑧∠A+∠B=90°
边角关系
sinA=cosB=cosA=sinB=tanA=
INCLUDEPICTURE"考点4.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点4.TIF"
\
MERGEFORMAT
解直角三角形的应用
仰角、俯角
在视线与水平线所成的锐角中,视线在水平线上方的角叫⑨__仰角__,视线在水平线下方的角叫⑩__俯角__.如图①
坡度(坡比)、坡角
坡面的铅直高度h和 __水平宽度__l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角.i=tanα= ____.如图②
方位角
指北或指南方向线与目标方向线所成的小于90°的水平角,叫做 __方位角__,如图③,A点位于O点的北偏东30°方向,B点位于O点的南偏东60°方向,C点位于O点的北偏西45°方向(或西北方向)
【规律总结】解直角三角形的方法:(1)解直角三角形,当所求元素不在直角三角形中时,应作辅助线构造直角三角形,或寻找已知直角三角形中的边角替代所要求的元素;(2)解实际问题的关键是构造几何模型,大多数问题都需要添加适当的辅助线,将问题转化为直角三角形中的边角计算问题.
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
锐角三角函数及特殊角三角函数值
【例1】(2016攀枝花中考)在△ABC中,如果∠A,∠B满足|tanA-1|+=0,那么∠C=________.
【解析】先根据非负性,得tanA=1,cosB=,求出∠A及∠B的度数,进而可得出结论.
∵在△ABC中,tanA=1,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=180°-∠A-∠B=75°.
【学生解答】75°
【点拨】熟记各特殊角度的三角函数值是解答此题的关键.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016唐山九中一模)在△ABC中,若+=0,则∠C的度数是( D )
A.30°
B.45°
C.60°
D.90°
2.(2016温州中考)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( D )
A.
B.
C.
D.
3.(2016无锡中考)sin30°的值为( A )
A.
B.
C.
D.
4.(2016孝感中考)式子2cos30°-tan45°-的值是( B )
A.2-2
B.0
C.2
D.2
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
解直角三角形的实际应用
【例2】(2016钦州中考)如图,在电线杆CD上的C处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6
m的B处安置高为1.5
m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
【解析】由题意可先过点A作AH⊥CD于点H,在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
【学生解答】解:如图,过点A作AH⊥CD,垂足为H,
由题意,可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6.
在Rt△ACH中,tan∠CAH=,
∴CH=AH·tan∠CAH=6tan30°=6×=2(m).
∵DH=1.5,∴CD=2+1.5,
在Rt△CDE中,∠CED=60°,sin∠CED=,
∴CE==4+≈5.7(m),
∴拉线CE的长约为5.7
m.
【方法总结】解此类题的一般方法:(1)作出辅助线,构造直角三角形;(2)利用锐角三角函数将各边之间的关系表示出来;(3)根据已知条件求值.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016石家庄十一中二模)如图,某公园入口处原有三级台阶,每级台阶高为18
cm,宽为30
cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是__210__cm.
(第5题图)
(第6题图)
6.(2016河北石家庄二十八中一模)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20
n
mile到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于__10__n
mile.
7.(2016保定十七中二模)如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2
cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为__2.7__cm.(结果精确到0.1
cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
8.(2016邢台中学二模)如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2km.有一艘小船在点P处,从A处测得小船的北偏西60°的方向,从B处测得小船的北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B处测得小船在北偏西15°的方向,求点C与点B这间的距离.(上述2小题的结果都保留根号)
解:(1)如图,过点P作PD⊥AB于点D.设PD=x
km.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x.在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,∴AD=PD=x.
∵BD+AD=AB,∴x+x=2,x=-1.∴点P到海岸线l的距离为(-1)km;
(2)如图,过点B作BF⊥AC于点F.根据题意,得∠ABC=105°,在Rt△ABF中,∠AFB=90°,∠BAF=30°,∴BF=AB=1.在△ABC中,∠C=180°-∠BAC-∠ABC=45°.在Rt△BCF中,∠BFC=90°,∠C=45°,∴BC=BF=,∴点C与点B之间的距离为
km.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016山西中考)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( D )
A.2
B.
C.
D.
(第1题图)
(第2题图)
2.(2016济宁中考)如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=3
m,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10
m,则旗杆BC的高度为( A )
A.5
m
B.6
m
C.8
m
D.(3+)m
3.(2016乐山中考)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( C )
A.sinB=
B.sinB=
C.sinB=
D.sinB=
4.(2016永州中考)下列式子错误的是( D )
A.cos40°=sin50°
B.tan15°·tan75°=1
C.sin225°+cos225°=1
D.sin60°=2sin30°
5.(2016福州中考)如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( C )
A.(sinα,sinα)
B.(cosα,cosα)
C.(cosα,sinα)
D.(sinα,cosα)
6.(2016益阳中考)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等,小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( A )
A.
m
B.
m
C.
m
D.
m
(第6题图)
(第7题图)
7.(2016金华中考)一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4
m,楼梯宽度1
m,则地毯的面积至少需要( D )
A.
m2
B.
m2
C.m2
D.(4+4tanθ)m2
8.(2016重庆中考)如图所示,某办公大楼正前方有一根高度是15
m的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20
m,梯坎坡长BC是12
m,梯坎坡度i=1∶,则大楼AB的高度约为(精确到0.1
m,参考数据:≈1.41,≈1.73,≈2.45)( D )
A.30.6
m
B.32.1
m
C.37.9
m
D.39.4
m
(第8题图)
(第9题图)
9.(2016巴中中考)一个公共房门前的台阶高出地面1.2
m,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( B )
A.斜坡AB的坡度是10°
B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°
m
D.AB=
m
10.(2016绍兴中考)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6
m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果精确到1m,备用数据:≈1.7,≈1.4)
解:延长PQ交直线AB于点E.(1)∠BPQ=90°-60°=30°;(2)设PE=x
m.在直角△APE中,∠A=45°,则AE=PE=x
m;∵∠PBE=60°,∴∠BPE=30°;在直角△BPE中,BE=PE=x
m,∵AB=AE-BE=6
m,则x-x=6,解得x=9+3.则BE=(3+3)m,在直角△BEQ中,QE=BE=(3+3)=(3+)m.∴PQ=PE,QE=9+3-(3+)=6+2≈9(m).答:电线杆PQ的高度约为9
m.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
11.(2016长沙中考)如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120
m,则这栋楼的高度为( A )
A.160
m
B.120
m
C.300
m
D.160
m
(第11题图)
(第12题图)
12.(2016廊坊二模)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.927
2,sin46°≈0.719
3,sin22°≈0.374
6,sin44°≈0.694
7)( B )
A.22.48海里
B.41.68海里
C.43.16海里
D.55.63海里
13.(2016十堰中考)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位地东北方向,在后沿河岸走了30
m,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10
m.请根据这些数据求出河的宽度为__(30+10)__m.(结果保留根号)
14.(2016潍坊中考)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6
m,CD=4
m,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度.(结果保留根号)
解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,∴∠DCF=30°,又CD=4,
∴DF=2,CF==2,
由题意得∠E=30°,∴EF==2,
∴BE=BC+CF+EF=6+4,
∴AB=BE×tanE=(6+4)×=(2+4)m.
答:电线杆的高度为(2+4)m.
15.(2016广安中考)如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5
m,为了安全现要作一个不锈钢扶手AB及两根与FG垂直且长为1
m的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
(1)求点D与点C的高度DH;
(2)求所有不锈钢材料的总长度.(即AD+AB+BC的长,结果精确到0.1
m)
解:(1)DH=1.5×=1.2
m;
(2)过B作BM⊥AD于M,
在矩形BCHM中,MH=BC=1
m,
AM=AD+DH-MH=1
m+1.2
m-1
m=1.2
(m),
在Rt△AMB中,AB=≈3.0
m,
所以有不锈钢材料的总长度为1
m+3.0
m+1
m=5.0
(m).
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2015
9
认识方位角
考查方式依题意画出方位角
3
3
2014
22(3)
解直角三角形的应用
以三个垃圾存放点为背景,(3)通过解直角三角形求垃圾运送费用
4
4
2013
8
解直角三角形的应用
以航行、方向角为背景,利用解直角三角形求距离
3
3
2009
8
解直角三角形的应用
以手扶电梯为背景,利用解直角三角形求高度
2
2
2010、2011、2012、2016四年未考查
命题规律
纵观河北8年中考,锐角三角函数及解直角三角形,在中考中只出一题,题型多为选择和解答题,分值2~9分,难度中等,主要考查解直角三角形的应用的选择题和解答题形式各考查了2次,2015年考查了对方位角的认识,其中2010~2012年都未考查,2016年也没独立考查.
命题预测
预计2017年河北中考,仍然会考此知识点,命选择题可能性较大,也有可能出解答题,应强化训练不留死角
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点.TIF"
\
MERGEFORMAT
解直角三角形的应用(3次)
1.(2015河北9题3分)已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( D )
,A)
,B)
,C)
,D)
2.(2009河北8题2分)如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8
m,则乘电梯从点B到点C上升的高度h是( B )
A.
m
B.4
m
C.4
m
D.8
m
(第2题图)
(第3题图)
3.(2013河北8题3分)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( D )
A.40海里
B.60海里
C.70海里
D.80海里
4.(2016石家庄四十三中一模)已知sin6°=a,sin36°=b,则sin26°=( A )
A.a2
B.2a
C.b2
D.b
5.(2016定州模拟)如图,在Rt△ABC中,∠C=90°,AB=13,BC=12.则下列三角函数表示正确的是( A )
A.sinA=
B.cosA=
C.tanA=
D.tanB=
(第5题图)
(第6题图)
6.(2016唐山二模)如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( B )
A.
B.
C.
D.
(第7题图)
(第8题图)
7.(2016张家口一模)河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1∶(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( A )
A.5
m
B.10
m
C.15
m
D.10
m
8.(2016保定十三中二模)如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为__2__.
9.(2016张家口九中二模)芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引伸出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2
m,两拉索底端距离AD为20
m,请求出立柱BH的长.(结果精确到0.1
m,≈1.732)
解:设DH=x
m,
∵∠CDH=60°,∠H=90°,
∴CH=DH·sin60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,
解得x=10-,
∴BH=2+(10-)=10-1≈16.3(m).
答:立柱BH的长约为16.3
m.
10.(2016邯郸二十五中模拟)保护视力要求人写字时眼睛和笔端的距离应超过30
cm.
图(1)是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图(2)的△ABC.
已知BC=30
cm,AC=22
cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
解:他的这种坐姿不符合保护视力的要求,
理由:如图(2)所示:过点B作BD⊥AC于点D,
∵BC=30
cm,∠ACB=53°,
∴sin53°==≈0.8,
解得:BD=24,
cos53°=≈0.6,
解得DC=18,
∴AD=22-18=4(cm),
∴AB===<,
∴他的这种坐姿不符合保护视力的要求.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
锐角三角函数的概念
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b,则∠A的
正弦
sinA==①
余弦
cosA==②
正切
tanA==③
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
特殊角的三角函数值
三角函数
30°
45°
60°
sinα
④____
cosα
⑤____
tanα
⑥____
1
INCLUDEPICTURE"考点3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点3.TIF"
\
MERGEFORMAT
解直角三角形
解直角三角形常用的关系:在Rt△ABC中,∠C=90°,则
三边关系
⑦__a2+b2=c2__
两锐角关系
⑧∠A+∠B=90°
边角关系
sinA=cosB=cosA=sinB=tanA=
INCLUDEPICTURE"考点4.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点4.TIF"
\
MERGEFORMAT
解直角三角形的应用
仰角、俯角
在视线与水平线所成的锐角中,视线在水平线上方的角叫⑨__仰角__,视线在水平线下方的角叫⑩__俯角__.如图①
坡度(坡比)、坡角
坡面的铅直高度h和 __水平宽度__l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角.i=tanα= ____.如图②
方位角
指北或指南方向线与目标方向线所成的小于90°的水平角,叫做 __方位角__,如图③,A点位于O点的北偏东30°方向,B点位于O点的南偏东60°方向,C点位于O点的北偏西45°方向(或西北方向)
【规律总结】解直角三角形的方法:(1)解直角三角形,当所求元素不在直角三角形中时,应作辅助线构造直角三角形,或寻找已知直角三角形中的边角替代所要求的元素;(2)解实际问题的关键是构造几何模型,大多数问题都需要添加适当的辅助线,将问题转化为直角三角形中的边角计算问题.
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
锐角三角函数及特殊角三角函数值
【例1】(2016攀枝花中考)在△ABC中,如果∠A,∠B满足|tanA-1|+=0,那么∠C=________.
【解析】先根据非负性,得tanA=1,cosB=,求出∠A及∠B的度数,进而可得出结论.
∵在△ABC中,tanA=1,cosB=,
∴∠A=45°,∠B=60°,
∴∠C=180°-∠A-∠B=75°.
【学生解答】75°
【点拨】熟记各特殊角度的三角函数值是解答此题的关键.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016唐山九中一模)在△ABC中,若+=0,则∠C的度数是( D )
A.30°
B.45°
C.60°
D.90°
2.(2016温州中考)如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( D )
A.
B.
C.
D.
3.(2016无锡中考)sin30°的值为( A )
A.
B.
C.
D.
4.(2016孝感中考)式子2cos30°-tan45°-的值是( B )
A.2-2
B.0
C.2
D.2
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
解直角三角形的实际应用
【例2】(2016钦州中考)如图,在电线杆CD上的C处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6
m的B处安置高为1.5
m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
【解析】由题意可先过点A作AH⊥CD于点H,在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
【学生解答】解:如图,过点A作AH⊥CD,垂足为H,
由题意,可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6.
在Rt△ACH中,tan∠CAH=,
∴CH=AH·tan∠CAH=6tan30°=6×=2(m).
∵DH=1.5,∴CD=2+1.5,
在Rt△CDE中,∠CED=60°,sin∠CED=,
∴CE==4+≈5.7(m),
∴拉线CE的长约为5.7
m.
【方法总结】解此类题的一般方法:(1)作出辅助线,构造直角三角形;(2)利用锐角三角函数将各边之间的关系表示出来;(3)根据已知条件求值.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016石家庄十一中二模)如图,某公园入口处原有三级台阶,每级台阶高为18
cm,宽为30
cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是__210__cm.
(第5题图)
(第6题图)
6.(2016河北石家庄二十八中一模)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20
n
mile到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于__10__n
mile.
7.(2016保定十七中二模)如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2
cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为__2.7__cm.(结果精确到0.1
cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
8.(2016邢台中学二模)如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2km.有一艘小船在点P处,从A处测得小船的北偏西60°的方向,从B处测得小船的北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B处测得小船在北偏西15°的方向,求点C与点B这间的距离.(上述2小题的结果都保留根号)
解:(1)如图,过点P作PD⊥AB于点D.设PD=x
km.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=x.在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,∴AD=PD=x.
∵BD+AD=AB,∴x+x=2,x=-1.∴点P到海岸线l的距离为(-1)km;
(2)如图,过点B作BF⊥AC于点F.根据题意,得∠ABC=105°,在Rt△ABF中,∠AFB=90°,∠BAF=30°,∴BF=AB=1.在△ABC中,∠C=180°-∠BAC-∠ABC=45°.在Rt△BCF中,∠BFC=90°,∠C=45°,∴BC=BF=,∴点C与点B之间的距离为
km.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016山西中考)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( D )
A.2
B.
C.
D.
(第1题图)
(第2题图)
2.(2016济宁中考)如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=3
m,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10
m,则旗杆BC的高度为( A )
A.5
m
B.6
m
C.8
m
D.(3+)m
3.(2016乐山中考)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( C )
A.sinB=
B.sinB=
C.sinB=
D.sinB=
4.(2016永州中考)下列式子错误的是( D )
A.cos40°=sin50°
B.tan15°·tan75°=1
C.sin225°+cos225°=1
D.sin60°=2sin30°
5.(2016福州中考)如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( C )
A.(sinα,sinα)
B.(cosα,cosα)
C.(cosα,sinα)
D.(sinα,cosα)
6.(2016益阳中考)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等,小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( A )
A.
m
B.
m
C.
m
D.
m
(第6题图)
(第7题图)
7.(2016金华中考)一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4
m,楼梯宽度1
m,则地毯的面积至少需要( D )
A.
m2
B.
m2
C.m2
D.(4+4tanθ)m2
8.(2016重庆中考)如图所示,某办公大楼正前方有一根高度是15
m的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20
m,梯坎坡长BC是12
m,梯坎坡度i=1∶,则大楼AB的高度约为(精确到0.1
m,参考数据:≈1.41,≈1.73,≈2.45)( D )
A.30.6
m
B.32.1
m
C.37.9
m
D.39.4
m
(第8题图)
(第9题图)
9.(2016巴中中考)一个公共房门前的台阶高出地面1.2
m,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( B )
A.斜坡AB的坡度是10°
B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°
m
D.AB=
m
10.(2016绍兴中考)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6
m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果精确到1m,备用数据:≈1.7,≈1.4)
解:延长PQ交直线AB于点E.(1)∠BPQ=90°-60°=30°;(2)设PE=x
m.在直角△APE中,∠A=45°,则AE=PE=x
m;∵∠PBE=60°,∴∠BPE=30°;在直角△BPE中,BE=PE=x
m,∵AB=AE-BE=6
m,则x-x=6,解得x=9+3.则BE=(3+3)m,在直角△BEQ中,QE=BE=(3+3)=(3+)m.∴PQ=PE,QE=9+3-(3+)=6+2≈9(m).答:电线杆PQ的高度约为9
m.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
11.(2016长沙中考)如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120
m,则这栋楼的高度为( A )
A.160
m
B.120
m
C.300
m
D.160
m
(第11题图)
(第12题图)
12.(2016廊坊二模)如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.927
2,sin46°≈0.719
3,sin22°≈0.374
6,sin44°≈0.694
7)( B )
A.22.48海里
B.41.68海里
C.43.16海里
D.55.63海里
13.(2016十堰中考)在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位地东北方向,在后沿河岸走了30
m,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10
m.请根据这些数据求出河的宽度为__(30+10)__m.(结果保留根号)
14.(2016潍坊中考)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6
m,CD=4
m,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度.(结果保留根号)
解:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,∴∠DCF=30°,又CD=4,
∴DF=2,CF==2,
由题意得∠E=30°,∴EF==2,
∴BE=BC+CF+EF=6+4,
∴AB=BE×tanE=(6+4)×=(2+4)m.
答:电线杆的高度为(2+4)m.
15.(2016广安中考)如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5
m,为了安全现要作一个不锈钢扶手AB及两根与FG垂直且长为1
m的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
(1)求点D与点C的高度DH;
(2)求所有不锈钢材料的总长度.(即AD+AB+BC的长,结果精确到0.1
m)
解:(1)DH=1.5×=1.2
m;
(2)过B作BM⊥AD于M,
在矩形BCHM中,MH=BC=1
m,
AM=AD+DH-MH=1
m+1.2
m-1
m=1.2
(m),
在Rt△AMB中,AB=≈3.0
m,
所以有不锈钢材料的总长度为1
m+3.0
m+1
m=5.0
(m).
同课章节目录
