2017河北中考数学4.3等腰三角形与直角三角形教材知识梳理
文档属性
| 名称 | 2017河北中考数学4.3等腰三角形与直角三角形教材知识梳理 | 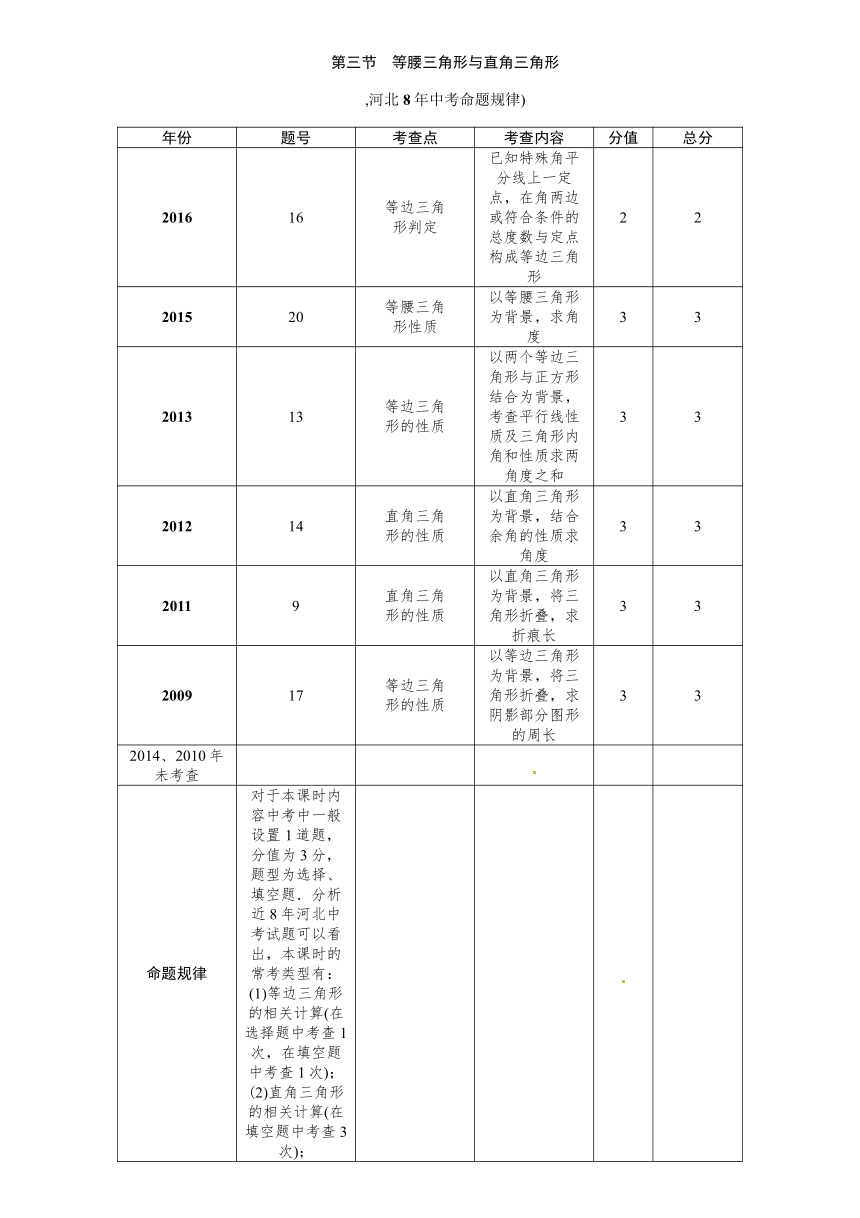 | |
| 格式 | zip | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-01 13:46:56 | ||
图片预览




文档简介
第三节 等腰三角形与直角三角形
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
16
等边三角形判定
已知特殊角平分线上一定点,在角两边或符合条件的总度数与定点构成等边三角形
2
2
2015
20
等腰三角形性质
以等腰三角形为背景,求角度
3
3
2013
13
等边三角形的性质
以两个等边三角形与正方形结合为背景,考查平行线性质及三角形内角和性质求两角度之和
3
3
2012
14
直角三角形的性质
以直角三角形为背景,结合余角的性质求角度
3
3
2011
9
直角三角形的性质
以直角三角形为背景,将三角形折叠,求折痕长
3
3
2009
17
等边三角形的性质
以等边三角形为背景,将三角形折叠,求阴影部分图形的周长
3
3
2014、2010年未考查
命题规律
对于本课时内容中考中一般设置1道题,分值为3分,题型为选择、填空题.分析近8年河北中考试题可以看出,本课时的常考类型有:(1)等边三角形的相关计算(在选择题中考查1次,在填空题中考查1次);(2)直角三角形的相关计算(在填空题中考查3次);(3)找符合条件的等边三角形(考查1次).
命题预测
纵观河北8年中考,2017年本节重点考查内容为直角三角形的相关计算,题型以填空题为主.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点1.TIF"
\
MERGEFORMAT
等边三角形判定和的相关计算
1.(2016河北16题2分)如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( D )
A.1个 B.2个
C.3个
D.3个以上
2.(2013河北13题3分)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( B )
A.90°
B.100°
C.130°
D.180°
(第2题图)
(第3题图)
3.(2009河北17题3分)如图,等边△ABC的边长为1
cm,D,E分别是AB,AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为__3__cm.
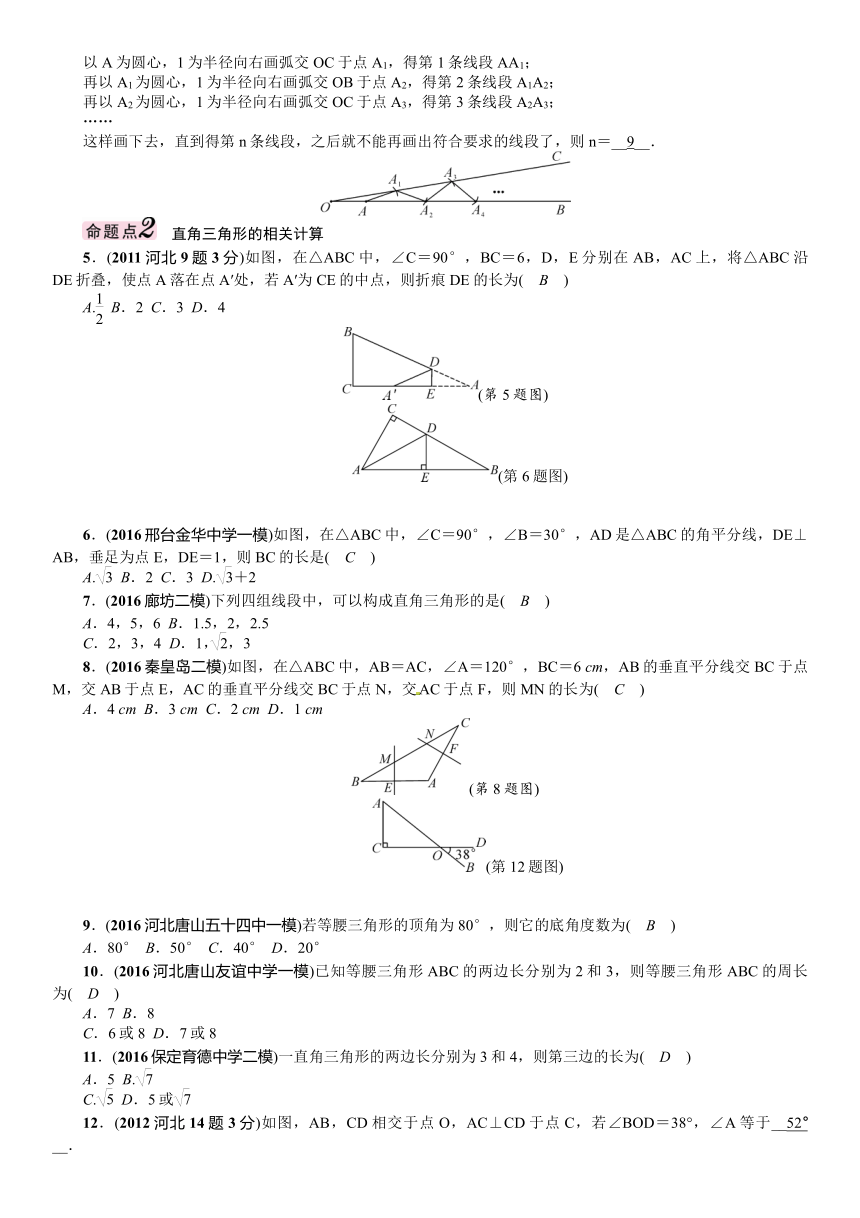
4.(2015河北20题3分)如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;
……
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=__9__.
INCLUDEPICTURE"命点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点2.TIF"
\
MERGEFORMAT
直角三角形的相关计算
5.(2011河北9题3分)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( B )
A.
B.2
C.3
D.4
(第5题图)
(第6题图)
6.(2016邢台金华中学一模)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC的长是( C )
A.
B.2
C.3
D.+2
7.(2016廊坊二模)下列四组线段中,可以构成直角三角形的是( B )
A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.1,,3
8.(2016秦皇岛二模)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( C )
A.4
cm
B.3
cm
C.2
cm
D.1
cm
(第8题图)
(第12题图)
9.(2016河北唐山五十四中一模)若等腰三角形的顶角为80°,则它的底角度数为( B )
A.80°
B.50°
C.40°
D.20°
10.(2016河北唐山友谊中学一模)已知等腰三角形ABC的两边长分别为2和3,则等腰三角形ABC的周长为( D )
A.7
B.8
C.6或8
D.7或8
11.(2016保定育德中学二模)一直角三角形的两边长分别为3和4,则第三边的长为( D )
A.5
B.
C.
D.5或
12.(2012河北14题3分)如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,∠A等于__52°__.
13.(2016唐山路北区二模)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
解:(1)∵△ABC是等边三角形,
∴∠B=60°,∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴ED=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
等腰三角形的性质与判定
1.等腰三角形
定义
有两边相等的三角形是等腰三角形,相等的两边叫腰,第三边为底
性质
(1)等腰三角形两腰相等(即AB=AC);(2)等腰三角形的两底角__相等__(即∠B=__∠C__);(3)等腰三角形是轴对称图形,有一条对称轴;(4)等腰三角形顶角的平分线、底边上的高和底边的中线互相重合;(5)面积:
S△ABC=BC·AD
判定
如果一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的角所对的边相等(简称“__等角对等边__”)
2.等边三角形
定义
三边相等的三角形是等边三角形
性质
(1)等边三角形三边相等(即AB=BC=AC);(2)等边三角形三角相等,且每一个角都等于__60°__(即∠A=∠B=∠C=__60°__);(3)等边三角形内、外心重合;(4)等边三角形是轴对称图形,有三条对称轴;(5)面积:S△ABC=BC·AD
判定
(1)三边都相等的三角形是等边三角形;(2)三个角相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
直角三角形的性质与判定(高频考点)
直角三角形的性质与判定近8年考查3次,题型均为填空题,设问方式为:1.求角度;2.求线段长度;3.求周长.结合的背景有:1.与三角形折叠结合;2.以赵爽弦图为背景;3.利用三角形余角的性质求角度.
3.直角三角形
定义
有一个角等于90°的三角形叫做直角三角形
性质
(1)直角三角形的两个锐角之和等于__90°__;(2)直角三角形斜边上的__中线__等于斜边的一半(即BD=AC);(3)直角三角形中__30°__角所对应的直角边等于斜边的一半(即AB=AC);(4)勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2;(5)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°
判定
(1)有一个角为90°的三角形是直角三角形;(2)一条边的中线等于这条边的一半的三角形是直角三角形;(3)有两个角互余的三角形是直角三角形
4.等腰直角三角形
定义
顶角为90°的等腰三角形是等腰直角三角形
性质
等腰直角三角形的顶角是直角,两底角为45°
判定
(1)用定义判定;(2)有两个角为45°的三角形
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
等腰三角形的相关计算
【例1】在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为50°,则底角∠B=________.
【学生解答】70°或20°
【点拨】在等腰三角形中,只要知道其中一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,必须分成两种情况来讨论.此题的两种情况如图所示:
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016湘西中考)一个等腰三角形一边长为4
cm,另一边长为5
cm,那么这个等腰三角形的周长是( C )
A.13
cm
B.14
cm
C.13
cm或14
cm
D.以上都不对
2.如图,在等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,且∠DBC=15°,则∠A=__50°__.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
等腰三角形、等边三角形的判定与性质
【例2】如图,在△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6
cm,DE=2
cm,则BC=________cm.
【解析】如图,延长AD交BC于点M,由AB=AC,AD是∠BAC的平分线可得AM⊥BC,BM=MC=BC,延长ED交BC于点N,则△BEN是等边三角形,从而求出DN的长,利用在直角三角形中,30°的角所对的直角边等于斜边的一半,求出MN的长,进而求BM,BC的值.
【学生解答】8
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
3.(2016沧州八中二模)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( D )
A.2个
B.3个
C.4个
D.5个
(第3题图)
(第4题图)
4.(2016漳州中考)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( C )
A.5个
B.4个
C.3个
D.2个
INCLUDEPICTURE"类型3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型3.TIF"
\
MERGEFORMAT
直角三角形的性质判定和勾股定理
【例3】如图,在Rt△ABC中,AB=AC,∠A=90°,D为BC上任意一点,DF⊥AB于点F,DE⊥AC于点E,M为BC的中点,连接EM,FM,给出以下五个结论:①AF=CE;②AE=BF;③△EFM是等腰直角三角形;④S四边形AEMF=S△ABC;⑤EF=BM=MC.当点D在BC上运动时(点D不与B,C重合),上述结论中始终正确的有( )
A.2个
B.3个
C.4个
D.5个
【解析】连接AM,易证AE=DF=BF,AF=DE=CE,△AME≌△BMF,∴ME=MF,∠AME=∠BMF,∴△EMF是等腰直角三角形.S四边形AEMF=S△AFM+S△AEM=S△AFM+S△BFM=S△ABM=S△ABC,但是EF与BM不一定相等,只有四边形AFME为矩形时,EF=BM.
【学生解答】C
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016株洲中考)如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四各情况的面积关系满足S1+S2=S3图形个数有( D )
A.1个
B.2个
C.3个
D.4个
6.(2016苏州中考)如图,长4
m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( B )
A.2
m
B.2
m
C.(2-2)m
D.(2-2)m
7.如图,在四边形ABCD中,AB⊥BC,AB=5,BC=12,AD=9,CD=5,求四边形ABCD的面积.
解:连接AC,∵AB⊥BC,∴∠B=90°,∴AC===13,
∵在△ACD中,AC2+AD2=132+92=169+81=250,CD2=(5)2=250,
∴AC2+AD2=CD2,∴∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ACD
=BC·AB+AD·AC
=×12×5+×9×13
=.
中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016秦皇岛二模)若实数x,y满足|x-4|+=0,则以x,y的值为两边长的等腰三角形的周长是( D )
A.12 B.16 C.16或20 D.20
2.(2016益阳中考)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( A )
A.
m
B.
m
C.
m
D.
m
3.(2016泰安中考)如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( D )
A.44°
B.66°
C.88°
D.92°
(第3题图)
(第4题图)
4.(2016沧州八中模拟)如图,在锐角三角形ABC中,AD,CE分别是边BC,AB上的高,垂足分别是D,E,AD,CE相交于点O,若∠B=60°,则∠AOE的度数是( A )
A.60°
B.50°
C.70°
D.80°
5.(2016保定十七中模拟)在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( D )
A.32
B.42
C.40或42
D.32或42
6.(2016宜昌中考)任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示,若连接EH,HF,FG,GE,则下列结论中,不一定正确的是( B )
A.△EGH为等腰三角形
B.△EGF为等边三角形
C.四边形EGFH为菱形
D.△EHF为等腰三角形
7.具备下列条件的△ABC中,不是直角三角形的是( D )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=∠B=3∠C
8.(2016深圳中考)如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( D )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
9.(2016杭州中考)已知直角三角形纸片的两条直角边分别为m和n(mA.m2+2mn+n2=0
B.m2-2mn+n2=0
C.m2+2mn-n2=0
D.m2-2mn-n2=0
10.(2016东营中考)在△ABC中,AB=10,AC=2,BC边上的高AD=6,则另一边BC等于( C )
A.10
B.8
C.6或10
D.8或10
11.(2016齐齐哈尔中考)有一面积为5的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为__20或20__.
12.在等边△ABC中,点E是AB上的动点,点E与点A,B不重合,点D在CB的延长线上,且EC=ED.
(1)当BE=AE时,求证:BD=AE;
(2)当BE≠AE时,“BD=AE”还成立吗?若你认为不成立,请直接写出BD与AE数量关系式,若你认为成立,请给予证明.
证明:(1)如图(1),在等边△ABC中,
∠ABC=∠ACB=60°.
∵BE=AE,∴∠ACE=∠ECB=30°.
又∵CE=DE,∴∠D=∠ECD=30°.
∴∠DEB=30°,∴BE=BD,∴BD=AE;
(2)BD=AE还成立.
理由如下:如图(2),过点E作EF∥AC交BC于点F.易证△EFB为等边三角形.
∴EF=FB=BE.∴∠EFB=∠EBF.
∴∠CFE=∠EBD.
∵CE=DE,∴∠ECD=∠D.∴△EBD≌△EFC(AAS),∴CF=BD.∵AB=BC,∴AB-BE=BF-CF,即AE=CF,∴BD=AE.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
13.(2016威海中考)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( B )
A.68°
B.88°
C.90°
D.112°
,(第13题图)) ,(第15题图))
14.(2016内江中考)已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( B )
A.
B.
C.
D.不能确定
15.(2016连云港中考)如图①,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图②,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( C )
A.86
B.64
C.54
D.48
16.(2016随州中考)如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN=__3__.
(第16题图)
(第18题图)
17.(2016潍坊中考)已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是__2__.
18.(2016武汉中考)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5,则BD的长为__2__.
19.(2016邯郸十一中一模)如图,∠ABC=90°,D,E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
证明:(1)∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF.
又∵∠ABC=90°,
∴∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
又∵∠DFC=∠AFM=90°,
∴△DFC≌△AFM,∴CF=MF.
∴∠FMC=∠FCM;
(2)AD⊥MC.理由:
由(1)知∠MFC=90°,FD=FE,FM=FC.
∴∠FDE=∠FMC=45°.
∴DE∥CM,由题意得AD⊥DE,∴AD⊥MC.
20.(2016北京中考)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
解:(1)在△ACD中,∵M,N分别是AC,CD的中点,∴MN∥AD且MN=AD.
在Rt△ABC中,∵M是AC的中点.
∴BM=AC.又∵AC=AD,∴MN=BM;
(2)∵∠BAD=60°且AC平分∠BAD.
∴∠BAC=∠DAC=30°.
由(1)知,BM=AC=AM=MC.
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.
∵MN∥AD,∴∠NMC=∠DAC=30°.
∴∠BMN=∠BMC+∠NMC=90°.
∴BN2=BM2+MN2.而由(1)知,
MN=BM=AC=×2=1,BN=.
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
16
等边三角形判定
已知特殊角平分线上一定点,在角两边或符合条件的总度数与定点构成等边三角形
2
2
2015
20
等腰三角形性质
以等腰三角形为背景,求角度
3
3
2013
13
等边三角形的性质
以两个等边三角形与正方形结合为背景,考查平行线性质及三角形内角和性质求两角度之和
3
3
2012
14
直角三角形的性质
以直角三角形为背景,结合余角的性质求角度
3
3
2011
9
直角三角形的性质
以直角三角形为背景,将三角形折叠,求折痕长
3
3
2009
17
等边三角形的性质
以等边三角形为背景,将三角形折叠,求阴影部分图形的周长
3
3
2014、2010年未考查
命题规律
对于本课时内容中考中一般设置1道题,分值为3分,题型为选择、填空题.分析近8年河北中考试题可以看出,本课时的常考类型有:(1)等边三角形的相关计算(在选择题中考查1次,在填空题中考查1次);(2)直角三角形的相关计算(在填空题中考查3次);(3)找符合条件的等边三角形(考查1次).
命题预测
纵观河北8年中考,2017年本节重点考查内容为直角三角形的相关计算,题型以填空题为主.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点1.TIF"
\
MERGEFORMAT
等边三角形判定和的相关计算
1.(2016河北16题2分)如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( D )
A.1个 B.2个
C.3个
D.3个以上
2.(2013河北13题3分)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( B )
A.90°
B.100°
C.130°
D.180°
(第2题图)
(第3题图)
3.(2009河北17题3分)如图,等边△ABC的边长为1
cm,D,E分别是AB,AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为__3__cm.
4.(2015河北20题3分)如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;
……
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=__9__.
INCLUDEPICTURE"命点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点2.TIF"
\
MERGEFORMAT
直角三角形的相关计算
5.(2011河北9题3分)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( B )
A.
B.2
C.3
D.4
(第5题图)
(第6题图)
6.(2016邢台金华中学一模)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC的长是( C )
A.
B.2
C.3
D.+2
7.(2016廊坊二模)下列四组线段中,可以构成直角三角形的是( B )
A.4,5,6
B.1.5,2,2.5
C.2,3,4
D.1,,3
8.(2016秦皇岛二模)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( C )
A.4
cm
B.3
cm
C.2
cm
D.1
cm
(第8题图)
(第12题图)
9.(2016河北唐山五十四中一模)若等腰三角形的顶角为80°,则它的底角度数为( B )
A.80°
B.50°
C.40°
D.20°
10.(2016河北唐山友谊中学一模)已知等腰三角形ABC的两边长分别为2和3,则等腰三角形ABC的周长为( D )
A.7
B.8
C.6或8
D.7或8
11.(2016保定育德中学二模)一直角三角形的两边长分别为3和4,则第三边的长为( D )
A.5
B.
C.
D.5或
12.(2012河北14题3分)如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,∠A等于__52°__.
13.(2016唐山路北区二模)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.
解:(1)∵△ABC是等边三角形,
∴∠B=60°,∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴ED=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
等腰三角形的性质与判定
1.等腰三角形
定义
有两边相等的三角形是等腰三角形,相等的两边叫腰,第三边为底
性质
(1)等腰三角形两腰相等(即AB=AC);(2)等腰三角形的两底角__相等__(即∠B=__∠C__);(3)等腰三角形是轴对称图形,有一条对称轴;(4)等腰三角形顶角的平分线、底边上的高和底边的中线互相重合;(5)面积:
S△ABC=BC·AD
判定
如果一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的角所对的边相等(简称“__等角对等边__”)
2.等边三角形
定义
三边相等的三角形是等边三角形
性质
(1)等边三角形三边相等(即AB=BC=AC);(2)等边三角形三角相等,且每一个角都等于__60°__(即∠A=∠B=∠C=__60°__);(3)等边三角形内、外心重合;(4)等边三角形是轴对称图形,有三条对称轴;(5)面积:S△ABC=BC·AD
判定
(1)三边都相等的三角形是等边三角形;(2)三个角相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
直角三角形的性质与判定(高频考点)
直角三角形的性质与判定近8年考查3次,题型均为填空题,设问方式为:1.求角度;2.求线段长度;3.求周长.结合的背景有:1.与三角形折叠结合;2.以赵爽弦图为背景;3.利用三角形余角的性质求角度.
3.直角三角形
定义
有一个角等于90°的三角形叫做直角三角形
性质
(1)直角三角形的两个锐角之和等于__90°__;(2)直角三角形斜边上的__中线__等于斜边的一半(即BD=AC);(3)直角三角形中__30°__角所对应的直角边等于斜边的一半(即AB=AC);(4)勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2;(5)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°
判定
(1)有一个角为90°的三角形是直角三角形;(2)一条边的中线等于这条边的一半的三角形是直角三角形;(3)有两个角互余的三角形是直角三角形
4.等腰直角三角形
定义
顶角为90°的等腰三角形是等腰直角三角形
性质
等腰直角三角形的顶角是直角,两底角为45°
判定
(1)用定义判定;(2)有两个角为45°的三角形
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
等腰三角形的相关计算
【例1】在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为50°,则底角∠B=________.
【学生解答】70°或20°
【点拨】在等腰三角形中,只要知道其中一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,必须分成两种情况来讨论.此题的两种情况如图所示:
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016湘西中考)一个等腰三角形一边长为4
cm,另一边长为5
cm,那么这个等腰三角形的周长是( C )
A.13
cm
B.14
cm
C.13
cm或14
cm
D.以上都不对
2.如图,在等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,且∠DBC=15°,则∠A=__50°__.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
等腰三角形、等边三角形的判定与性质
【例2】如图,在△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6
cm,DE=2
cm,则BC=________cm.
【解析】如图,延长AD交BC于点M,由AB=AC,AD是∠BAC的平分线可得AM⊥BC,BM=MC=BC,延长ED交BC于点N,则△BEN是等边三角形,从而求出DN的长,利用在直角三角形中,30°的角所对的直角边等于斜边的一半,求出MN的长,进而求BM,BC的值.
【学生解答】8
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
3.(2016沧州八中二模)如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( D )
A.2个
B.3个
C.4个
D.5个
(第3题图)
(第4题图)
4.(2016漳州中考)如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( C )
A.5个
B.4个
C.3个
D.2个
INCLUDEPICTURE"类型3.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型3.TIF"
\
MERGEFORMAT
直角三角形的性质判定和勾股定理
【例3】如图,在Rt△ABC中,AB=AC,∠A=90°,D为BC上任意一点,DF⊥AB于点F,DE⊥AC于点E,M为BC的中点,连接EM,FM,给出以下五个结论:①AF=CE;②AE=BF;③△EFM是等腰直角三角形;④S四边形AEMF=S△ABC;⑤EF=BM=MC.当点D在BC上运动时(点D不与B,C重合),上述结论中始终正确的有( )
A.2个
B.3个
C.4个
D.5个
【解析】连接AM,易证AE=DF=BF,AF=DE=CE,△AME≌△BMF,∴ME=MF,∠AME=∠BMF,∴△EMF是等腰直角三角形.S四边形AEMF=S△AFM+S△AEM=S△AFM+S△BFM=S△ABM=S△ABC,但是EF与BM不一定相等,只有四边形AFME为矩形时,EF=BM.
【学生解答】C
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
5.(2016株洲中考)如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四各情况的面积关系满足S1+S2=S3图形个数有( D )
A.1个
B.2个
C.3个
D.4个
6.(2016苏州中考)如图,长4
m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( B )
A.2
m
B.2
m
C.(2-2)m
D.(2-2)m
7.如图,在四边形ABCD中,AB⊥BC,AB=5,BC=12,AD=9,CD=5,求四边形ABCD的面积.
解:连接AC,∵AB⊥BC,∴∠B=90°,∴AC===13,
∵在△ACD中,AC2+AD2=132+92=169+81=250,CD2=(5)2=250,
∴AC2+AD2=CD2,∴∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ACD
=BC·AB+AD·AC
=×12×5+×9×13
=.
中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016秦皇岛二模)若实数x,y满足|x-4|+=0,则以x,y的值为两边长的等腰三角形的周长是( D )
A.12 B.16 C.16或20 D.20
2.(2016益阳中考)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1
m,则旗杆PA的高度为( A )
A.
m
B.
m
C.
m
D.
m
3.(2016泰安中考)如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( D )
A.44°
B.66°
C.88°
D.92°
(第3题图)
(第4题图)
4.(2016沧州八中模拟)如图,在锐角三角形ABC中,AD,CE分别是边BC,AB上的高,垂足分别是D,E,AD,CE相交于点O,若∠B=60°,则∠AOE的度数是( A )
A.60°
B.50°
C.70°
D.80°
5.(2016保定十七中模拟)在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( D )
A.32
B.42
C.40或42
D.32或42
6.(2016宜昌中考)任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示,若连接EH,HF,FG,GE,则下列结论中,不一定正确的是( B )
A.△EGH为等腰三角形
B.△EGF为等边三角形
C.四边形EGFH为菱形
D.△EHF为等腰三角形
7.具备下列条件的△ABC中,不是直角三角形的是( D )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=∠B=3∠C
8.(2016深圳中考)如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( D )
A.∠2=60°
B.∠3=60°
C.∠4=120°
D.∠5=40°
9.(2016杭州中考)已知直角三角形纸片的两条直角边分别为m和n(m
B.m2-2mn+n2=0
C.m2+2mn-n2=0
D.m2-2mn-n2=0
10.(2016东营中考)在△ABC中,AB=10,AC=2,BC边上的高AD=6,则另一边BC等于( C )
A.10
B.8
C.6或10
D.8或10
11.(2016齐齐哈尔中考)有一面积为5的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为__20或20__.
12.在等边△ABC中,点E是AB上的动点,点E与点A,B不重合,点D在CB的延长线上,且EC=ED.
(1)当BE=AE时,求证:BD=AE;
(2)当BE≠AE时,“BD=AE”还成立吗?若你认为不成立,请直接写出BD与AE数量关系式,若你认为成立,请给予证明.
证明:(1)如图(1),在等边△ABC中,
∠ABC=∠ACB=60°.
∵BE=AE,∴∠ACE=∠ECB=30°.
又∵CE=DE,∴∠D=∠ECD=30°.
∴∠DEB=30°,∴BE=BD,∴BD=AE;
(2)BD=AE还成立.
理由如下:如图(2),过点E作EF∥AC交BC于点F.易证△EFB为等边三角形.
∴EF=FB=BE.∴∠EFB=∠EBF.
∴∠CFE=∠EBD.
∵CE=DE,∴∠ECD=∠D.∴△EBD≌△EFC(AAS),∴CF=BD.∵AB=BC,∴AB-BE=BF-CF,即AE=CF,∴BD=AE.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
13.(2016威海中考)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( B )
A.68°
B.88°
C.90°
D.112°
,(第13题图)) ,(第15题图))
14.(2016内江中考)已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( B )
A.
B.
C.
D.不能确定
15.(2016连云港中考)如图①,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图②,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( C )
A.86
B.64
C.54
D.48
16.(2016随州中考)如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD=BD,连接DM,DN,MN.若AB=6,则DN=__3__.
(第16题图)
(第18题图)
17.(2016潍坊中考)已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是__2__.
18.(2016武汉中考)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5,则BD的长为__2__.
19.(2016邯郸十一中一模)如图,∠ABC=90°,D,E分别在BC,AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
证明:(1)∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF.
又∵∠ABC=90°,
∴∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
又∵∠DFC=∠AFM=90°,
∴△DFC≌△AFM,∴CF=MF.
∴∠FMC=∠FCM;
(2)AD⊥MC.理由:
由(1)知∠MFC=90°,FD=FE,FM=FC.
∴∠FDE=∠FMC=45°.
∴DE∥CM,由题意得AD⊥DE,∴AD⊥MC.
20.(2016北京中考)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
解:(1)在△ACD中,∵M,N分别是AC,CD的中点,∴MN∥AD且MN=AD.
在Rt△ABC中,∵M是AC的中点.
∴BM=AC.又∵AC=AD,∴MN=BM;
(2)∵∠BAD=60°且AC平分∠BAD.
∴∠BAC=∠DAC=30°.
由(1)知,BM=AC=AM=MC.
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.
∵MN∥AD,∴∠NMC=∠DAC=30°.
∴∠BMN=∠BMC+∠NMC=90°.
∴BN2=BM2+MN2.而由(1)知,
MN=BM=AC=×2=1,BN=.
同课章节目录
