2017河北中考数学4.5多边形与平行四边形教材知识梳理
文档属性
| 名称 | 2017河北中考数学4.5多边形与平行四边形教材知识梳理 |
|
|
| 格式 | zip | ||
| 文件大小 | 318.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-01 00:00:00 | ||
图片预览




文档简介
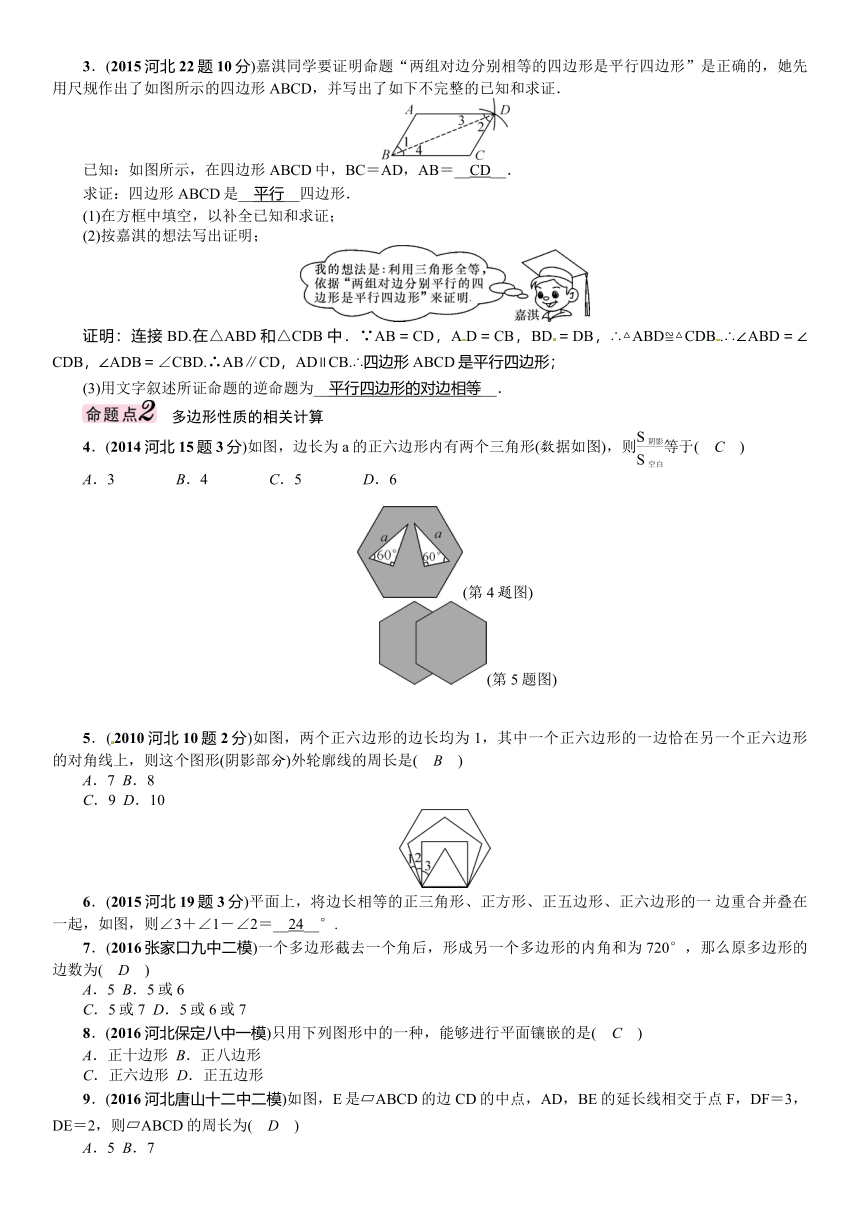
第五节 多边形与平行四边形
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
13
平行四边形性质
将平行四边形按某方式折叠求某角度数
2
2
2015
19
正多边形的性质
以正三角形,正四边形、正五边形、正六边形为背景,求角的度数
3
22
平行四边形的判定
利用三角形全等让两组对边分别相等,得平行四边形
10
13
2014
15
正六边形的性质
以正六边形为背景,涉及两个含60°角的直角三角形,求阴影部分与空白部分的面积比
3
3
2012
9
平行四边形的性质
以平行四边形的折叠为背景,利用平行四边形的性质,求角度
3
18
正多边形的性质
通过正八边形拼接,利用正八边形的内角和公式求多边形的个数
3
22(1)
平行四边形的性质
平行四边形与反比例函数、一次函数结合,根据平行四边形的性质,求反比例函数的解析式
4
10
2011
23(3)
平行四边形的性质
以正方形为背景,猜想四边形为平行四边形,并且予以证明
3
3
2010
10
正六边形的性质
两个正六边形部分重叠,求图形外轮廓线的周长
2
2
2013、2009年未考查
命题规律
平行四边形与多边形在河北中考中最多设置3道题,分值为2~10分.分析近8年河北中考试题可以看出,本课时常考类型有:(1)平行四边形判定及性质的相关计算(在选择题中考查1次,在解答题中考查2次);(2)多边形性质的相关计算(在选择题中考查2次,在填空题中考查2次).
命题预测
预计2017年中考,仍会以平行四边形相关知识为主,也会与其他知识结合.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点1.TIF"
\
MERGEFORMAT
平行四边形的判定及性质的相关计算
1.(2016河北13题2分)如图,将 ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( C )
A.66° B.104°
C.114°
D.124°
2.(2012河北9题3分)如图,在 ABCD中,∠A=70°,将 ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上).折痕为MN,则∠AMF等于( B )
A.70°
B.40°
C.30°
D.20°
3.(2015河北22题10分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图所示,在四边形ABCD中,BC=AD,AB=__CD__.
求证:四边形ABCD是__平行__四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
证明:连接BD.在△ABD和△CDB中.∵AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB.∴∠ABD=∠CDB,∠ADB=∠CBD.∴AB∥CD,AD∥CB.∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为__平行四边形的对边相等__.
INCLUDEPICTURE"命点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点2.TIF"
\
MERGEFORMAT
多边形性质的相关计算
4.(2014河北15题3分)如图,边长为a的正六边形内有两个三角形(数据如图),则等于( C )
A.3 B.4 C.5 D.6
(第4题图)
(第5题图)
5.(2010河北10题2分)如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( B )
A.7
B.8
C.9
D.10
6.(2015河北19题3分)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一
边重合并叠在一起,如图,则∠3+∠1-∠2=__24__°.
7.(2016张家口九中二模)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( D )
A.5
B.5或6
C.5或7
D.5或6或7
8.(2016河北保定八中一模)只用下列图形中的一种,能够进行平面镶嵌的是( C )
A.正十边形
B.正八边形
C.正六边形
D.正五边形
9.(2016河北唐山十二中二模)如图,E是 ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则 ABCD的周长为( D )
A.5
B.7
C.10
D.14
(第9题图)
(第10题图)
10.(2016河北石家庄四十一中一模)如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2=__225°__.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
多边形
1.
n边形(n≥3)
内角和定理
n边形的内角和为(n-2)·180°
外角和定理
n边形的外角和为__360°__
对角线
过n(n>3)边形一个顶点可引(n-3)条对角线,n边形共有条对角线
正n边形n≥3
定义
在平面内,边相等,角也相等的多边形叫做正多边形
性质
(1)正n边形的每一个内角为____
(2)正(2n-1)边形是轴对称图形,对称轴有(2n-1)条;正2n边形既是轴对称图形,又是中心对称图形,对称轴有2n条
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
平行四边形的性质与判定(高频考点)
图(1)
近8年平行四边形的性质考查3次,考查题型为选择题、解答题,考查类型有2种:①以折叠为背景利用平行四边形的性质求角度;②与函数结合利用平行四边形的性质求函数解析式.
2.定义:两组对边分别平行的四边形叫做平行四边形.如图(1)所示.
3.性质
文字描述
字母表示[参考图(1)]
(1)对边平行且相等
AB綊CD,AD綊BC
(2)对角相等
∠DAB=∠DCB,∠ADC=∠ABC
(3)对角线互相平分
OA=OC,OB=OD
(4)平行四边形是中心对称图形,对称中心是两条对角线的交点,O为对称中心
4.判定
文字描述
字母表示[参考图(1)]
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)一组对边平行且相等的四边形是平行四边形
(4)两组对角分别相等的四边形是平行四边形
四边形ABCD是平行四边形
(5)两条对角线互相平分的四边形是平行四边形
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
多边形的相关计算
【例1】(2016龙岩中考)一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
A.四边形 B.五边形
C.六边形
D.七边形
【学生解答】C
【点拨】n边形的内角和为(n-2)·180,与边数n有关;外角和为360°,与n无关.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016广安中考)若一个正n边形的每个内角都为144°,则这个正n边形的所有对角线的条数是( C )
A.7
B.10
C.35
D.70
2.(2016莱芜中考)若一个正多边形的每个内角为156°,则这个正多边形的边数是( C )
A.13
B.14
C.15
D.16
3.(2016梅州中考)若凸多边形的内角和为1
260°,则该多边形的对角线有__27__条.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
平行四边形的相关计算
【例2】(2017中考预测)已知,如图,在 ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【解析】(1)利用ASA即可得证;(2)运用平行四边形的性质和判定解决.
【学生解答】证明:(1)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∴∠EAM=∠FCN.
又∵AD∥BC,∴∠E=∠F.
∵AE=CF,∴△AEM≌△CFN;
(2)由(1)得AM=CN,又∵四边形ABCD是平行四边形.∴AB綊CD,∴BM綊DN,
∴四边形BMDN是平行四边形.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
4.(2016黔东南中考)如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( A )
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
(第4题图)
(第5题图)
5.(2016丽水中考)如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( B )
A.13
B.17
C.20
D.26
6.(2016益阳中考)如图,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.
求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD.
又∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF.
∴△AED≌△CFB.
∴AE=CF.
∴四边形AECF是平行四边形,
∴AF=CE.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016临沂中考)一个正多边形内角和等于540°,则这个正多边形的每一个外角等于( C )
A.108°
B.90°
C.72°
D.60°
2.(2016湘西中考)下列说法错误的是( D )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.(2016舟山中考)已知一个正多边形的内角是140°,则这个正多边形的边数是( D )
A.6
B.7
C.8
D.9
4.(2016菏泽中考)在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( B )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
5.(2016孝感中考)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( D )
A.3
B.5
C.2或3
D.3或5
6.(2016石家庄一模)平行四边形ABCD与等边△AEF如图放置,如果∠B=45°,那么∠BAE的大小是( A )
A.75°
B.70°
C.65°
D.60°
7.(2016北京中考)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=__360°__.
(第7题图)
(第8题图)
8.(2016江西中考)如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为__50°__.
9.(2016达州中考)如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( B )
A.2
B.3
C.4
D.5
(第9题图)
(第10题图)
10.(2016河南中考)如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数是__110°__.
11.(2016攀枝花中考)如果一个正多边形的每个外角都是30°,那么这个多边形的内角和为__1__800°__.
12.(2016邵阳中考)如图所示,点E,F是平行四边形ABCD对角线BD上的点,BF=DE,求证:AE=CF.
证明:∵四边形ABCD是平行四边形.
∴AD∥BC,AD=BC.
∴∠EDA=∠FBC.在△AED和△CFB中,
∴△AED≌△CFB(SAS),∴AE=CF.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
13.(2015唐山二模)如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,三角形FCB的周长为28,则FC的长为( C )
A.4
B.5
C.6
D.7
(第13题图)
(第14题图)
14.(2015石家中四十三中模拟)如图,在 ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( D )
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
15.(2016南充中考)如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:
①∠AME=108°;②AN2=AM·AD;③MN=3-;④S△EBC=2-1.其中正确结论的个数是( C )
A.1个
B.2个
C.3个
D.4个
16.(2016白银中考)如图,已知EC∥AB,∠EDA=∠ABF.
求证:(1)四边形ABCD为平行四边形;
(2)OA2=OE·OF.
证明:(1)∵EC∥AB,∴∠C=∠ABF,
又∵∠EDA=∠ABF,∴∠C=∠EDA.
∴AD∥BC.∴四边形ABCD为平行四边形;
(2)∵EC∥AB,∴=.
又∵AD∥BC,∴=,∴=,
∴OA2=OE·OF.
17.(2016长沙中考)如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
解:(1)∵四边形ABCD为平行四边形,
∴AB=DC.
∴∠DAC=∠BCA.
又∵∠BAC=∠DAC,∴∠BAC=∠BCA.
∴△ABC为等腰三角形,∴AB=BC;
(2)连接BD交AC于点O,
∵AB=BC,且四边形ABCD为平行四边形.
∴四边形ABCD为菱形,∴AC⊥BD.
∵BO2+=AB2,
∴BO2+=22.
∴BO=1且BD=2BO=2.
∴S ABCD=BD·AC=×2×2=2.
18.(2016邯郸十一中二模)如图(1),在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于点E.
(1)求证:四边形ABCE是平行四边形;
(2)如图(2),将图(1)中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
解:(1)∵在Rt△OAB中,D为OB的中点,∴AD=OB,OD=BD=OB,DO=DA,∴∠DAO=∠DOA=30°,∴∠EOA=∠DOC+∠DOA=90°,∴∠AEO=60°,又∵△OBC为等边三角形,
∴∠BCO=∠AEO=60°,∴BC∥AE,
∵∠BAO=∠COA=90°,∴CO∥AB,
∴四边形ABCE是平行四边形;
(2)OG=1.
19.(2016石家庄四十二中)已知M,N分别为△ABC的边AC,BC的中点,AN,BM交于点O,E为OB的中点.
(1)如图(1),若F为OA的中点,求证:MF綊NE;
(2)如图(2),若AB=BC,AM=6,NE=,求AB的长.
解:(1)连接OC.
∵点M是AC的中点,
∴点F是AO的中点.
∴MF是△AOC的中位线,
∴MF綊OC,
同理可证.
NE綊OC.
∴MF綊NE;
(2)易证NE=OC,∴OC=2.
利用三线合一,易求CM=AM=6.
∴OM=4.
取OA的中点F,
易证四边形MFEN为平行四边形.
∴OM=OE=4,
∵E为OB的中点,∴BE=4,
∴BM=12,∴AB=6.
20.如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
求证:(1)四边形MNCD是平行四边形;
(2)BD=MN.
证明:(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC,∵M,N分别是AD,BC的中点,∴MD=NC,MD∥NC,∴MNCD是平行四边形;(2)如图,连接ND,∵MNCD是平行四边形,∴MN=DC.∵N是BC的中点,∴BN=CN,∵BC=2CD,∠C=60°,∴△NCD是等边三角形.∴ND=NC,∠DNC=60°.∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC,∵DN=NC=NB,∴∠DBN=∠BDN=∠DNC=30°,∴∠BDC=90°.∵tan∠DBC==,∴DB=DC=MN.
,河北8年中考命题规律)
年份
题号
考查点
考查内容
分值
总分
2016
13
平行四边形性质
将平行四边形按某方式折叠求某角度数
2
2
2015
19
正多边形的性质
以正三角形,正四边形、正五边形、正六边形为背景,求角的度数
3
22
平行四边形的判定
利用三角形全等让两组对边分别相等,得平行四边形
10
13
2014
15
正六边形的性质
以正六边形为背景,涉及两个含60°角的直角三角形,求阴影部分与空白部分的面积比
3
3
2012
9
平行四边形的性质
以平行四边形的折叠为背景,利用平行四边形的性质,求角度
3
18
正多边形的性质
通过正八边形拼接,利用正八边形的内角和公式求多边形的个数
3
22(1)
平行四边形的性质
平行四边形与反比例函数、一次函数结合,根据平行四边形的性质,求反比例函数的解析式
4
10
2011
23(3)
平行四边形的性质
以正方形为背景,猜想四边形为平行四边形,并且予以证明
3
3
2010
10
正六边形的性质
两个正六边形部分重叠,求图形外轮廓线的周长
2
2
2013、2009年未考查
命题规律
平行四边形与多边形在河北中考中最多设置3道题,分值为2~10分.分析近8年河北中考试题可以看出,本课时常考类型有:(1)平行四边形判定及性质的相关计算(在选择题中考查1次,在解答题中考查2次);(2)多边形性质的相关计算(在选择题中考查2次,在填空题中考查2次).
命题预测
预计2017年中考,仍会以平行四边形相关知识为主,也会与其他知识结合.
,河北8年中考真题及模拟)
INCLUDEPICTURE"命点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点1.TIF"
\
MERGEFORMAT
平行四边形的判定及性质的相关计算
1.(2016河北13题2分)如图,将 ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( C )
A.66° B.104°
C.114°
D.124°
2.(2012河北9题3分)如图,在 ABCD中,∠A=70°,将 ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上).折痕为MN,则∠AMF等于( B )
A.70°
B.40°
C.30°
D.20°
3.(2015河北22题10分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图所示,在四边形ABCD中,BC=AD,AB=__CD__.
求证:四边形ABCD是__平行__四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
证明:连接BD.在△ABD和△CDB中.∵AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB.∴∠ABD=∠CDB,∠ADB=∠CBD.∴AB∥CD,AD∥CB.∴四边形ABCD是平行四边形;
(3)用文字叙述所证命题的逆命题为__平行四边形的对边相等__.
INCLUDEPICTURE"命点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/命点2.TIF"
\
MERGEFORMAT
多边形性质的相关计算
4.(2014河北15题3分)如图,边长为a的正六边形内有两个三角形(数据如图),则等于( C )
A.3 B.4 C.5 D.6
(第4题图)
(第5题图)
5.(2010河北10题2分)如图,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是( B )
A.7
B.8
C.9
D.10
6.(2015河北19题3分)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一
边重合并叠在一起,如图,则∠3+∠1-∠2=__24__°.
7.(2016张家口九中二模)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( D )
A.5
B.5或6
C.5或7
D.5或6或7
8.(2016河北保定八中一模)只用下列图形中的一种,能够进行平面镶嵌的是( C )
A.正十边形
B.正八边形
C.正六边形
D.正五边形
9.(2016河北唐山十二中二模)如图,E是 ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则 ABCD的周长为( D )
A.5
B.7
C.10
D.14
(第9题图)
(第10题图)
10.(2016河北石家庄四十一中一模)如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2=__225°__.
,中考考点清单)
INCLUDEPICTURE"考点1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点1.TIF"
\
MERGEFORMAT
多边形
1.
n边形(n≥3)
内角和定理
n边形的内角和为(n-2)·180°
外角和定理
n边形的外角和为__360°__
对角线
过n(n>3)边形一个顶点可引(n-3)条对角线,n边形共有条对角线
正n边形n≥3
定义
在平面内,边相等,角也相等的多边形叫做正多边形
性质
(1)正n边形的每一个内角为____
(2)正(2n-1)边形是轴对称图形,对称轴有(2n-1)条;正2n边形既是轴对称图形,又是中心对称图形,对称轴有2n条
INCLUDEPICTURE"考点2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/考点2.TIF"
\
MERGEFORMAT
平行四边形的性质与判定(高频考点)
图(1)
近8年平行四边形的性质考查3次,考查题型为选择题、解答题,考查类型有2种:①以折叠为背景利用平行四边形的性质求角度;②与函数结合利用平行四边形的性质求函数解析式.
2.定义:两组对边分别平行的四边形叫做平行四边形.如图(1)所示.
3.性质
文字描述
字母表示[参考图(1)]
(1)对边平行且相等
AB綊CD,AD綊BC
(2)对角相等
∠DAB=∠DCB,∠ADC=∠ABC
(3)对角线互相平分
OA=OC,OB=OD
(4)平行四边形是中心对称图形,对称中心是两条对角线的交点,O为对称中心
4.判定
文字描述
字母表示[参考图(1)]
(1)两组对边分别平行的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)一组对边平行且相等的四边形是平行四边形
(4)两组对角分别相等的四边形是平行四边形
四边形ABCD是平行四边形
(5)两条对角线互相平分的四边形是平行四边形
,中考重难点突破)
INCLUDEPICTURE"类型1.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型1.TIF"
\
MERGEFORMAT
多边形的相关计算
【例1】(2016龙岩中考)一个多边形的内角和是它的外角和的2倍,则这个多边形是( )
A.四边形 B.五边形
C.六边形
D.七边形
【学生解答】C
【点拨】n边形的内角和为(n-2)·180,与边数n有关;外角和为360°,与n无关.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
1.(2016广安中考)若一个正n边形的每个内角都为144°,则这个正n边形的所有对角线的条数是( C )
A.7
B.10
C.35
D.70
2.(2016莱芜中考)若一个正多边形的每个内角为156°,则这个正多边形的边数是( C )
A.13
B.14
C.15
D.16
3.(2016梅州中考)若凸多边形的内角和为1
260°,则该多边形的对角线有__27__条.
INCLUDEPICTURE"类型2.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/类型2.TIF"
\
MERGEFORMAT
平行四边形的相关计算
【例2】(2017中考预测)已知,如图,在 ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【解析】(1)利用ASA即可得证;(2)运用平行四边形的性质和判定解决.
【学生解答】证明:(1)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∴∠EAM=∠FCN.
又∵AD∥BC,∴∠E=∠F.
∵AE=CF,∴△AEM≌△CFN;
(2)由(1)得AM=CN,又∵四边形ABCD是平行四边形.∴AB綊CD,∴BM綊DN,
∴四边形BMDN是平行四边形.
INCLUDEPICTURE"针对.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/针对.TIF"
\
MERGEFORMAT
4.(2016黔东南中考)如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( A )
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
(第4题图)
(第5题图)
5.(2016丽水中考)如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( B )
A.13
B.17
C.20
D.26
6.(2016益阳中考)如图,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.
求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD.
又∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF.
∴△AED≌△CFB.
∴AE=CF.
∴四边形AECF是平行四边形,
∴AF=CE.
,中考备考方略)
INCLUDEPICTURE"基础训练.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/基础训练.TIF"
\
MERGEFORMAT
1.(2016临沂中考)一个正多边形内角和等于540°,则这个正多边形的每一个外角等于( C )
A.108°
B.90°
C.72°
D.60°
2.(2016湘西中考)下列说法错误的是( D )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.(2016舟山中考)已知一个正多边形的内角是140°,则这个正多边形的边数是( D )
A.6
B.7
C.8
D.9
4.(2016菏泽中考)在 ABCD中,AB=3,BC=4,当 ABCD的面积最大时,下列结论正确的有( B )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
5.(2016孝感中考)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( D )
A.3
B.5
C.2或3
D.3或5
6.(2016石家庄一模)平行四边形ABCD与等边△AEF如图放置,如果∠B=45°,那么∠BAE的大小是( A )
A.75°
B.70°
C.65°
D.60°
7.(2016北京中考)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=__360°__.
(第7题图)
(第8题图)
8.(2016江西中考)如图所示,在 ABCD中,∠C=40°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为__50°__.
9.(2016达州中考)如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( B )
A.2
B.3
C.4
D.5
(第9题图)
(第10题图)
10.(2016河南中考)如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数是__110°__.
11.(2016攀枝花中考)如果一个正多边形的每个外角都是30°,那么这个多边形的内角和为__1__800°__.
12.(2016邵阳中考)如图所示,点E,F是平行四边形ABCD对角线BD上的点,BF=DE,求证:AE=CF.
证明:∵四边形ABCD是平行四边形.
∴AD∥BC,AD=BC.
∴∠EDA=∠FBC.在△AED和△CFB中,
∴△AED≌△CFB(SAS),∴AE=CF.
INCLUDEPICTURE"能力提升.TIF"INCLUDEPICTURE
"../../../../../../中考王——河北数学/中考王%20%20河北数学Word/能力提升.TIF"
\
MERGEFORMAT
13.(2015唐山二模)如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,三角形FCB的周长为28,则FC的长为( C )
A.4
B.5
C.6
D.7
(第13题图)
(第14题图)
14.(2015石家中四十三中模拟)如图,在 ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( D )
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
15.(2016南充中考)如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,给出下列结论:
①∠AME=108°;②AN2=AM·AD;③MN=3-;④S△EBC=2-1.其中正确结论的个数是( C )
A.1个
B.2个
C.3个
D.4个
16.(2016白银中考)如图,已知EC∥AB,∠EDA=∠ABF.
求证:(1)四边形ABCD为平行四边形;
(2)OA2=OE·OF.
证明:(1)∵EC∥AB,∴∠C=∠ABF,
又∵∠EDA=∠ABF,∴∠C=∠EDA.
∴AD∥BC.∴四边形ABCD为平行四边形;
(2)∵EC∥AB,∴=.
又∵AD∥BC,∴=,∴=,
∴OA2=OE·OF.
17.(2016长沙中考)如图,AC是 ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
(2)若AB=2,AC=2,求 ABCD的面积.
解:(1)∵四边形ABCD为平行四边形,
∴AB=DC.
∴∠DAC=∠BCA.
又∵∠BAC=∠DAC,∴∠BAC=∠BCA.
∴△ABC为等腰三角形,∴AB=BC;
(2)连接BD交AC于点O,
∵AB=BC,且四边形ABCD为平行四边形.
∴四边形ABCD为菱形,∴AC⊥BD.
∵BO2+=AB2,
∴BO2+=22.
∴BO=1且BD=2BO=2.
∴S ABCD=BD·AC=×2×2=2.
18.(2016邯郸十一中二模)如图(1),在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于点E.
(1)求证:四边形ABCE是平行四边形;
(2)如图(2),将图(1)中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
解:(1)∵在Rt△OAB中,D为OB的中点,∴AD=OB,OD=BD=OB,DO=DA,∴∠DAO=∠DOA=30°,∴∠EOA=∠DOC+∠DOA=90°,∴∠AEO=60°,又∵△OBC为等边三角形,
∴∠BCO=∠AEO=60°,∴BC∥AE,
∵∠BAO=∠COA=90°,∴CO∥AB,
∴四边形ABCE是平行四边形;
(2)OG=1.
19.(2016石家庄四十二中)已知M,N分别为△ABC的边AC,BC的中点,AN,BM交于点O,E为OB的中点.
(1)如图(1),若F为OA的中点,求证:MF綊NE;
(2)如图(2),若AB=BC,AM=6,NE=,求AB的长.
解:(1)连接OC.
∵点M是AC的中点,
∴点F是AO的中点.
∴MF是△AOC的中位线,
∴MF綊OC,
同理可证.
NE綊OC.
∴MF綊NE;
(2)易证NE=OC,∴OC=2.
利用三线合一,易求CM=AM=6.
∴OM=4.
取OA的中点F,
易证四边形MFEN为平行四边形.
∴OM=OE=4,
∵E为OB的中点,∴BE=4,
∴BM=12,∴AB=6.
20.如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
求证:(1)四边形MNCD是平行四边形;
(2)BD=MN.
证明:(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC,∵M,N分别是AD,BC的中点,∴MD=NC,MD∥NC,∴MNCD是平行四边形;(2)如图,连接ND,∵MNCD是平行四边形,∴MN=DC.∵N是BC的中点,∴BN=CN,∵BC=2CD,∠C=60°,∴△NCD是等边三角形.∴ND=NC,∠DNC=60°.∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC,∵DN=NC=NB,∴∠DBN=∠BDN=∠DNC=30°,∴∠BDC=90°.∵tan∠DBC==,∴DB=DC=MN.
同课章节目录
